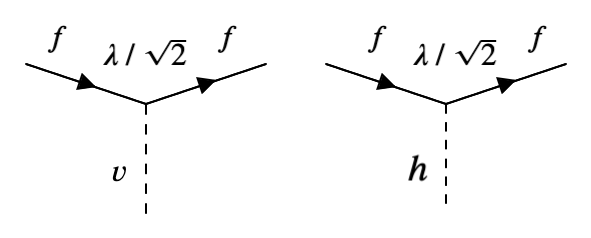5. Sobre el Modelo Estándar#

import time
print(' Last version ', time.asctime() )

 Last version  Mon Oct 27 14:58:57 2025

# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2

# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

import scipy.constants as units

5.1. Objetivos#

Conocer:

  • Los elementos principales de la unificación electrodébil.

  • La física principal del bosón \(Z\). La anchura de desintegración del \(Z\) y la existencia de tres neutrinos.

  • Los elementos que permiten que el bosón de Higgs dote de la masa de los fermiones.

  • El descubrimiento del bosón de Higgs.

5.2. Introducción#

El Modelo Estándar (SM) es uno de los grandes logros de la Física del siglo XX. Describe con gran precisión todos los resultados experimentales obtenidos en Física de Partículas, con la excepción de los fenómenos de oscilación de neutrinos.

No obstante sabemos que el modelo es incompleto, ya que no explica ciertos aspectos fundamentales del Universo, como la asimetría materia–antimateria o la naturaleza de la materia oscura.

El SM se construye a partir de varios principios esenciales:

  • El modelo debe incorporar las partículas e interacciones conocidas, y respetar las leyes de conservación observadas experimentalmente. En particular, debe reproducir hechos empíricos como la violación de paridad en las corrientes débiles cargadas.

  • Debe estar formulado mediante un lagrangiano invariante de Lorentz y unitario, en cumplimiento de los principios de la relatividad especial y la mecánica cuántica.

  • Las interacciones entre fermiones y campos vectoriales emergen de la invariancia gauge local del lagrangiano. Este principio, central en la teoría cuántica de campos, garantiza la renormalizabilidad de la teoría: que las cantidades físicas observables sean finitas y bien definidas.

  • Finalmente, el mecanismo de Higgs proporciona una forma coherente de generar la masa de los bosones \(W^\pm\) y \(Z\), así como de los fermiones, sin romper la invariancia gauge fundamental del modelo.

5.2.1. Hitos de la creacción del SM#

  • 1961–1967 — Formulación de la teoría electrodébil por S. Glashow, A. Salam y S. Weinberg, unificando las interacciones electromagnética y débil.

  • 1964 — Desarrollo del mecanismo de Higgs por F. Englert y R. Brout, y de forma independiente por P. Higgs, introduciendo el campo y el bosón asociados a la ruptura espontánea de simetría gauge.

  • 1973 — Descubrimiento de las corrientes neutras en el experimento Gargamelle (CERN), confirmando una de las predicciones clave del modelo electrodébil.

  • 1973 — G. ’t Hooft y M. Veltman demuestran la renormalizabilidad de las teorías gauge con rotura de simetría mediante el mecanismo de Higgs, consolidando la consistencia matemática del Modelo Estándar.

  • 1983 — C. Rubbia y colaboradores (en el experimento UA1, CERN) descubren los bosones \(W^\pm\) y \(Z\), las partículas mediadoras de la interacción débil.

  • Década de 1990 — Los experimentos de precisión en LEP (CERN) confirman las predicciones del Modelo Estándar, incluyendo la física del bosón \(Z\) y la existencia de tres familias de neutrinos.

  • 2012 — Descubrimiento del bosón de Higgs por los experimentos ATLAS y CMS del LHC (CERN), completando el esquema del Modelo Estándar.

5.3. Unificación electrodébil#

5.3.1. El descubrimiento de las corrientes neutras#

En los años 60 se sospechaba de la posible existencia de un nuevo mediador débil neutro, el bosón vectorial \(Z\). En particular la sección eficaz del proceso \(e^+ + e \to W^+ + W^-\) crecía infinitamente con la energía si en su cálculo solo intervenía como mediador el fotón, pero si se consideraba la mediación de un \(Z\), la sección eficaz se moderaba y alcazaba un valor máximo.

La predición más genuina de la presencia de un \(Z\) era la existencia de corrientes débiles neutras, y de forma límpia entre neutrinos. Los neutrinos podrían ahora interactuar débilmente con la materia, mediante el \(Z\), y, si tenían suficiente energía, romper los nucleones y producir hadrones sin dar lugar a su leptón cargado asociado:

\[ \nu_\mu + N \to \nu_\mu + \mathrm{hadrones} \]

donde \(N\) es un nucleón.

Gargamelle , en el CERN, en los años 70, fue el experimento que observó por primera vez las corrientes neutras. Utilizando un haz compuesto principalmente por \(\nu_\mu\), estudió las interacciones de estos neutrinos con los nucleones del blanco.

  • En las corrientes cargadas, los neutrinos producían un \(\mu\), una partícula altamente penetrante: $\( \nu_\mu + N \to \mu + X \)$

  • En las corrientes neutras, el neutrino escapaba indetectado, pero la ruptura del nucleón dejaba trazas observables:

\[ \nu_\mu + N \to \nu_\mu + X \]

donde \(X\) representa los posibles hadrones.

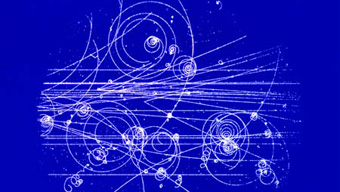
Gargamelle era una gran cámara de burbujas ubicada en un campo magnético, donde se tomaban fotografías sincronizadas con la llegada del haz de neutrinos.

La figura muestra una de las primeras corrientes neutras observada. A la llegada del neutrino se produce un puñado de trazas y ningún muón.

../_images/sm_gargamelle_event.jpeg

Evento de corriente neutra observado en Gargamelle [CERN]

Las mediciones de la frecuencia con las que suceden las corrientes neutras con respecto a las cargadas que realizó Gargamelle mostraron un buen acuerdo con las prediciones del modelo estándar y supusieron la primera confirmación seria de la vigencia del mismo.

5.3.2. La interacción electromagnética y la invariancia gauge#

Vamos ahora a introducir brevemente el modelo estándar, dar unas pautas de cómo surgen los bosones vectoriales y sus interacciones débiles y cargadas.

A partir de este punto es necesario introducir los lagrangianos.

Los lagrangianos y las ecuaciones del movimiento de los campos libres son:

—– Tipo —–

—– Escalar Complejo ——

——– Espinor ——–

– Bosón vectorial —–

Klein-Gordon

Dirac

Maxwell

Ecuación

\((\partial^\mu\partial_\mu + m^2) \, \phi = 0\)

\((i\gamma^\mu \partial_\mu - m) \, \Psi = 0\)

\(\partial_\mu F^{\mu\nu} = 0\)

Lagrangiano

\((\partial_\mu \phi)^* (\partial^\mu \phi) - m^2 \phi^* \phi\)

\(i\bar{\Psi}\gamma^\mu \partial_\mu \Psi - m \bar{\Psi}\Psi\)

\(-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}\)

Donde:

\[ F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu \]

Pero la física interesante sucede en la interacción entre los campos.

La interacción electromagnética surge al exigir que el lagrangiano de fermiones sea invariance gauge local.

Podemos verificar fácilmente que el lagragiano de Dirac es invariante bajo una cambio de fase global \(\theta\) en el espinor \(\Psi(x)\).

\[ \Psi'(x) \to e^{i q\, \theta} \,\, \Psi(x) \]

donde \(q\) es la carga eléctrica del fermión.

Para que el lagrangiano sea invariante bajo una transformación local, esto es, con un cambio de fase que depende localmente, \(\theta(x)\),

\[ \Psi'(x) \to e^{i q\, \theta(x)} \, \Psi(x) \]

Debemos considerar conjuntamente la existencia del campo fermiónico con el del campo vectorial de fotón.

Para ello, debemos sustituir la derivada covariante por la derivada covariante generalizada.

\[ D_\mu = \partial_\mu + i q A_\mu \]

El lagrangiano conjunto del fermión cargado y el fotón es:

\[\begin{split} \mathcal{L} = i \bar{\Psi} \gamma^\mu D_\mu \Psi - m \bar{\Psi} \Psi - \frac{1}{4} F_{\mu\nu}F^{\mu\nu} \\ = i \bar{\Psi} \gamma^\mu \partial_\mu \Psi - q \, \bar{\Psi} \gamma^\mu \Psi A_\mu - m \bar{\Psi}\Psi- \frac{1}{4} F_{\mu\nu}F^{\mu\nu} \end{split}\]

Aquí, \(q\), es la carga eléctrica del fermión.

De esta forma, la interacción con el fotón emerge de la simetría, y no se introduce “a mano”, cumpliendo el principio fundamental de invarianza gauge.

ejercicio: Verifica que el lagrangiano anterior es efectivamente invariante gauge local.

Usar que la parte del campo vectorial no se ve afectado por un cambio:

\[ A'_\mu(x) = A_\mu(x) - \partial_\mu \theta(x) \]

En el lagrangiano, el término:

\[ q \bar{\Psi} \gamma^\mu \Psi \, A_\mu \]

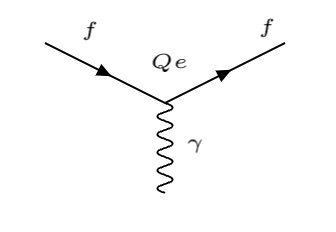
corresponde a la interacción entre un fermión cargado con carga \(q\) y el fotón, y tiene asociado el siguiente vértice de los diagramas de Feynman.

../_images/sm_emcur.png

vértice electromagnético \(Q\), es la carga eléctrica en unidades de \(e\)

La corriente fermíonica \(\bar{\Psi}\gamma^\mu \Psi\) se acompla con un fotón \(A_\mu\) con una intensidad dada por su carga \(q = Qe\) (dende \(e\) es la carga eléctrica y \(Q\) la carga del fermión en unidades de \(e\)).

Decimos que el lagrangiano tiene una simetría \(U(1)\), o es invariante, bajo un cambio de fase.

G. t’Hooft demostró que los lagrangianos con invariance gauge local son renormalizables, esto es, al cuantificar los campos y calcular las secciones eficaces se pueden obtener resultados finitos.

5.3.3. Teoría electro-débil#

Respecto a las interacciones débiles cargadas, mediadas por los \(W^\pm\), sabemos que:

  • Solo intervienen los espinores de quiralidad izquierda.

  • Siempre aparecen en pares. En la primera familia, los pares son:

    \[\begin{split} \begin{pmatrix} \nu_e \\ e \end{pmatrix}, \;\;\; \begin{pmatrix} u \\ d \end{pmatrix} \end{split}\]

Para preservar los dos hechos anteriores, la teoría electrodébil se construye a partir de:

  • considerar que los fermiones no tienen masa -por el momento-

  • situar los espinores de izquierdas en un duplete de un espacio interno que llamaremos isospín débil de \(SU(2)\) y los de derechas en singletes:

\[\begin{split} L \equiv \begin{pmatrix} \Psi^{\nu_e}_L \\ \Psi^{e}_L \end{pmatrix}; \;\; \Psi^{e}_R \end{split}\]
\[\begin{split} Q \equiv \begin{pmatrix} \Psi^{u}_L \\ \Psi^{d}_L \end{pmatrix}; \;\; \Psi^{u}_R, \,\Psi^{d}_R \end{split}\]

Notar que, por construcción, el neutrino solo tiene componente de quiralidad a izquierdas. Y también que los fermiones deben carecer de masa para poder separar las dos componentes de quiralidad en campos independientes.

Con esta configuración, el lagrangiano de la primera familia de leptones se puede escrbir como:

\[ i\bar{L} \gamma^\mu \partial_\mu L + i \bar{\Psi}^e_R \gamma^\mu \partial_\mu \Psi^e_R \]

El primer término es un producto escalar entre dos dupletes.

Recodemos que no hay término de masas, ya que consideramos fermiones sin masa.

Si desarrollamos el primer término, el asociado al duplete, obtenemos:

\[\begin{split} i \bar{L} \gamma^\mu \partial_\mu L = i \begin{pmatrix} \bar{\Psi}^{\nu}_L, \bar{\Psi}^{e}_L \end{pmatrix} \gamma^\mu \partial_\mu \begin{pmatrix} \Psi^{\nu}_L \\ \Psi^{e}_L \end{pmatrix} = \\ i \bar{\Psi}^{\nu}_L \gamma^\mu \partial_\mu \Psi^{\nu}_L + i \gamma^\mu \bar{\Psi}^{e}_L \gamma^\mu \partial_\mu \Psi^{e}_L \\ \end{split}\]

Si añadimos ahora de nuevo el segundo término, el asociado al singlete, obtenemos:

\[ i \bar{\Psi}^{\nu}_L \gamma^\mu \partial_\mu \Psi^{\nu}_L + i \gamma^\mu \bar{\Psi}^{e}_L \gamma^\mu \partial_\mu \Psi^{e}_L + i \gamma^\mu \bar{\Psi}^{e}_R \gamma^\mu \partial_\mu \Psi^{e}_R \]

donde hemos usado que:

\[ \bar{\Psi}^{e} \gamma^\mu \partial_\mu \Psi^e = \bar{\Psi}^{e}_L \gamma^\mu \partial_\mu \Psi^{e}_L + \bar{\Psi}^{e}_R \gamma^\mu \partial_\mu \Psi^{e}_R \]

de esta forma, recuperamos la forma inicial del lagrangiano de Dirac para un neutrino y un electrón sin masa:

\[ i \bar{\Psi}^{\nu}_L \gamma^\mu \partial_\mu \Psi^{\nu}_L + i \bar{\Psi}^{e} \gamma^\mu \partial_\mu \Psi^e \]

El lagrangiano de la primera familia, la parte del duplete,

\[ i\bar{L} \gamma^\mu \partial_\mu L + i \bar{\Psi}^e_R \gamma^\mu \partial_\mu \Psi^e_R \]

es ahora invariante bajo cuatro cambios de fase:

del grupo \(U(1)\)

del grupo \(SU(2)\)

\(L' = e^{i\theta} \, L\)

\(L' = e^{i\theta_i \frac{\sigma^i}{2}} \, L\)

Recordemos que el generador de las rotaciones en \(U(1)\) es la identidad, 1, y en \(SU(2)\) los generadores son las matrices de Pauli \(\sigma^i/2\).

cuestión: verificar que el lagrangiano anterior es invariante

Respecto a la rotación \(U(\theta)\):

\[ U(\theta) = e^{i\theta_i \frac{\sigma^i}{2}} \]
\[ L' = U(\theta) \, L, \;\; \bar{L}' = U^\dagger(\theta) L \]

luego $\( i \bar{L}' \gamma^\mu \partial_\mu L' = i \bar{L} U^\dagger \gamma^\mu U \partial_\mu L = i \bar{L} U^\dagger U \gamma_\mu \partial_\mu L = i \bar{L} \gamma^\mu \partial_\mu L \)$

dado que:

\[ U^\dagger U = I \]

Exigiendo que la invariancia del lagrangiano sera local, para cada una de las posibles fases aparece ahora un campo vectorial y la interacción entre el fermión y los campos.

Omitimos aquí el desarrollo de la teoría electrodébil, que contiene detalles sutiles muy importantes, entre ellos cómo aparece en ángulo de Weinberg, (ver la extensión y [MT]), para indicar que los campos vectoriales físicos son:

\[ W_\mu^\pm, \, Z_\mu, \, A_\mu \]

Los \(W^\pm_\mu\) son bosones vectoriales cargados, con carga eléctrica \(\pm e\), y los campos \(Z_\mu, A_\mu\), son bosones vectoriales neutros. El campo \(A_\mu\) corresponde al fotón y \(Z_\mu\) al bosón vectorial neutro \(Z\).

La teoría electrodébil tiene solo dos parámetros:

  • La carga eléctrica, \(e\), -o si se prefiere la constante de estrucura fina, \(\alpha\)-.

  • El acoplo débil \(g_W\).

En vez de \(g_W\) en la Literatura se utiliza por razones históricas el ángulo de Weinberg, \(\theta_W\), cuyo valor se conoce con precisión:

\[ \sin^2 \theta_W = 0.23146 \pm 0.000012 \]

La relación de las constante de acoplo con \(e\) y \(\theta_W\) es

electromagnética

—— débil cargada ——–

——— débil neutra ————-

\(e\)

\(g_W = \frac{e}{\sin \theta_W}\)

\(g_Z = \frac{g_W}{\cos \theta_W} = \frac{e}{\sin \theta_W \cos \theta_W}\)

En el lagrangiano aparecen ahora cuatro términos de interacción entre cada uno de los campos bosónicos y los fermiones, que son:

corriente

———————- forma —————————–

electromagnética

\(Q e \, (\bar{\Psi} \gamma^\mu \Psi) \, A_\mu\)

débil cargada

\(\frac{g_W}{\sqrt{2}} (\bar{L} \gamma^\mu \sigma^+ L) \, W^+_\mu + \frac{g_W}{\sqrt{2}} (\bar{L} \gamma^\mu \sigma^- L) \, W^-_\mu\)

débil neutra

\(g_Z \left( c_L \, \bar{\Psi}_L \gamma^\mu \Psi_L + c_R \, \bar{\Psi}_R \gamma^\mu \Psi_R \right) \, Z_\mu \)

donde:

  • \(Q\) es la carga del fermión en unidades del electrón, esto es, \(-1\) para el electrón.

  • \(\sigma^\pm = (\sigma^1\pm i\sigma^2)/2\), son las matrices escalera que conectan los elementos de arriba con los de abajo del duplete.

  • \(c_L, c_R\), son dos coeficientes que dependen de la carga eléctrica del fermión y de su posición en el duplete.

Si desarrollamos el término de interacción débil cargada:

\[ \frac{g_W}{\sqrt{2}} (\bar{L} \gamma^\mu \sigma^+ L) \, W^+_\mu = \]

para la primera familia de leptones, recuperamos la expresión habitual de las interacciones débiles cargadas:

\[\begin{split} \frac{g_W}{\sqrt{2}} \begin{pmatrix} \bar{\Psi}^{\nu}_{L}, \bar{\Psi}^e_L \end{pmatrix} \, \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \gamma^\mu \begin{pmatrix} \Psi^\nu_L \\ \Psi^e_L \end{pmatrix} \, W^+_\mu= \frac{g_W}{\sqrt{2}} \bar{\Psi}^\nu_L \, \gamma^\mu \, \Psi^e_L \, W^+_\mu \end{split}\]

Vemos que, por construcción, la interacción débil cargada viola paridad de forma máxima, ya que solo intervienen los espinores a izquierdas.

Remarcar que las interacciones con el \(Z\) están completamente determinadas por el modelo.

Los coeficientes \(c_L, c_R\) son:

\[ c_L = T^3 - Q \sin^2 \theta_W, \;\; c_R = -Q \sin^2 \theta_W \]

Donde \(Q\) es la carga en unidades de electrón \(e\), esto es -1 para el electrón, y \(T^3\) es la tercera componente de isospín débil. Esto es, para el neutrino \(Q = 0\) y \(T^3 = 1/2\), y para el electrón \(Q = -1, \; T^3 = -1/2\).

La siguiente tabla muestra los coeficientes para la primera familia de leptones:

——– \(c_R\) ——–

——– \(c_L\) ——–

\(\nu_e\)

0

\(\frac{1}{2}\)

\(e\)

\(s^2_W\)

\(-\frac{1}{2} + s^2_W\)

donde \(s^2_W \equiv \sin^2 \theta_W\).

Podemos comprobar que en las corrientes neutras solo interviene nuevamente la componente de quiralidad a izquierdas del neutrino.

5.4. Física del \(Z\)#

5.4.1. Interacción \(e + e^+\)#

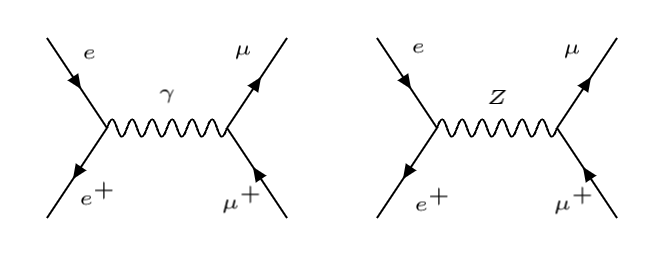
En la aniquilación \(e + e^+ \to \mu + \mu^+\) intervienen dos mediadores, el \(\gamma\) y el \(Z\). Nota que el portador debe ser necesariamente neutro.

La siguiente figura muestra los diagramas de Feynman de la aniquilación \(e+e^+ \to \mu+\mu^+\):

../_images/sm_gz.png

aniquilación \(e+e^+ \to \mu + \mu^+\) mediada por el fotón (izda) o el \(Z\) (derecha)

Los propagadores del fotón y del \(Z\) son:

\[ \frac{g_{\mu\nu}}{q^2}, \;\; \frac{g_{\mu\nu}}{q^2 - m_Z^2}, \]

donde \(m_Z = 91.2\) GeV es la masa del \(Z\), y \(q^2\) el cuadrado del cuadrimomento transferido del bosón.

Tenemos tres regímenes de \(q^2\) diferentes:

  • \(q^2 \ll m^2_Z\), en ese caso domina el propagador del fotón, la interacción es mayoritariamente electromagnética, y preserva paridad.

  • \(q^2 \sim m^2_Z\) domina el propagador del \(Z\), la interacción es mayoritariamente débil neutra, y cambia al pasar por el valor \(q^2 = m^2_Z\)

  • \(q^2 \gg m^2_Z\) los dos propagadores contribuyen con una fracción cada uno.

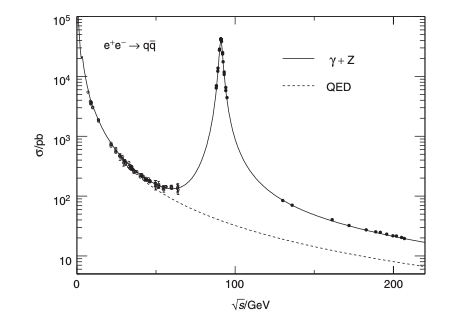
La figura muestra las medidas de la sección eficaz \(\sigma(e+e^+ \to \mathrm{hadrons})\) obtenidas por diversos experimentos y sobreimpuesta la curva teórica. Se muestra también la sección eficaz debida solo al fotón con la curva punteada.

../_images/sm_sigma_eeqq.png

\(\sigma(e+e^+ \to \mathrm{hadrons})\) vs \(\sqrt{s}\) de [MT16.2] [LEP-SLD]

Se observa que la contribución del fotón, es dominante a baja energía, que luego domina, en la resonancia, el \(Z\), y finalmente hay un equilibrio entre los dos bosones.

También que sería imposible explicar los datos experimentales sin la existencia del \(Z\) y que la predicción teórica está en excelente acuerdo con los datos.

5.4.2. Asimetría delante-atrás#

En la región donde el \(Z\) domine o sea relevante aparecen efectos de violación de paridad que dependerán de \(s^2_W\) en el proceso \(e+e^+ \to \mu +\mu^+\).

Consideramos el eje de choque \(e+e^+\) y tomamos la dirección hacia delante la que define el \(e\). Definimos la asimetría delante-atras, \(A_{FB}\), a partir del número de \(\mu\) que salen hacia delante, \(N_F\), (o forward) y hacia atrás, \(N_B\), (lo backwards) como:

\[ A_{FB} = \frac{N_F - N_B}{N_F + N_B} \]

Si se conserva paridad, debe cumplirse que \(A_{FB} = 0\)

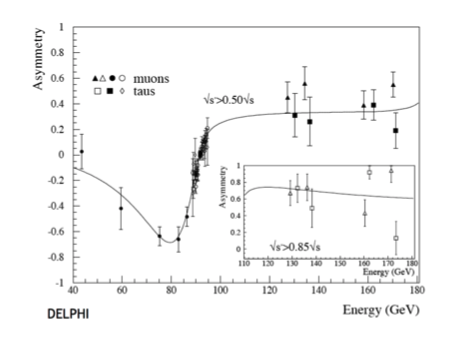
En la figura, se muestran los valores experimentales de la asimetría delante-atrás, \(A_{FB}\), obtenidos por el experimento DELPHI, en función de la energía en el centro de masas, o \(\sqrt{s}\), y sobreimpuesta se muestra la línea que corresponde a la predicción del Modelo Estandar para un valor de \(s^2_W \simeq 0.23\).

../_images/sm_afb.png

Asimetría forward-backward \(e+e^+ \to \mu + \mu^+\) vs \(\sqrt{s}\)

datos (puntos) del experimento [DELPHI] y predicción del SM para \(s^2_W \simeq 0.23\) (línea)

La medida de la asimetría delante-atrás confirma la teoría electrodébil y nos permite determinar \(s^2 \theta_W\) -o el ángulo de Weinberg-

5.4.3. Anchura de desintegración del \(Z\)#

En la década de los 90, El colisionador LEP \(e+e^+\) del CERN operó a \(\sqrt{s} = m_Z = 91\) GeV produciendo millones de \(Z\), lo que permitió estudar su física con gran precisión.

Uno de los resultados más importantes de LEP es la medida de la anchura de desintegración del \(Z\), que se obtienen a partir de la sección eficaz.

5.4.3.1. Sección eficaz#

La sección eficaz \(e+e^+ \to \mu + \mu^+\) en función del invariante \(s\) en la región dominada por el \(Z\) viene dada por: $\( \sigma (e+e^+\to Z \to \mu+\mu^+)= \frac{12 \pi s}{m^2_Z} \frac{\Gamma_{ee} \Gamma_{\mu\mu}}{(s-m^2_Z)^2 + m^2_Z\Gamma^2_Z} \)$

Donde \(m_Z, \, \Gamma_Z\) son la masa y la anchura de desintegración del \(Z\) respectivamente; y \(\Gamma_{ee}, \Gamma_{\mu\mu}\) son las anchuras parciales de desintegración del \(Z\) a \(e+e^+\) y \(\mu+\mu^+\) respectivamente -el Modelo Estandar predice que son iguales-.

La sección eficaz sigue una función de tipo Breit-Wigner donde:

  • existe un el polo, donde la sección eficaz es máxima, en \(\sqrt{s} = m_z\) $\( \sigma_{\max} = \frac{12\pi}{m^2_Z} \frac{\Gamma_{ee}\Gamma_{\mu\mu}}{\Gamma^2_Z} \)$

  • y en los valores \(\sqrt{s} = m_Z \pm \Gamma_Z/2\) la sección eficaz vale la mitad del máximo:

\[ \sigma \left(\sqrt{s} = m_Z \pm \Gamma_Z/2 \right) = \frac{\sigma_{\max}}{2} \]

o lo que es lo mismo, la anchura a mitad de altura, FWHM, es la anchura de desintegración \(\Gamma_Z\)

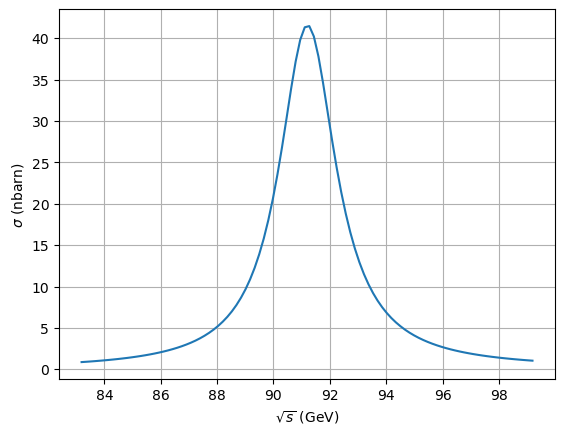
Cuestión Calcula el máximo de la sección eficaz para \(e+e^+\to \mu+\mu^+\) y \(e+e^+\to \mathrm{hadrones}\) y la curva se la sección eficaz para hadrones en el pico del \(Z\).

Gee = 0.0838 # GeV 
Gmm = 0.0838 # GeV
Gnn = 0.1657 # GeV
Guu = 0.2894 # GeV
Gdd = 0.3713 # GeV
Ghad = 2 * Guu + 3 * Gdd
Gtot = Ghad + 3 * Gee + 3 * Gnn
#print(Gtot)
mz  = 91.19  # GeV
Gz  =  2.45  # GeV
sigma_mumu = (12 * np.pi)/(mz**2) * (Gee * Gmm)/Gz**2
sigma_had  = (12 * np.pi)/(mz**2) * (Gee * Ghad)/Gz**2
sigma_tot  = (12 * np.pi)/(mz**2) * (Gee * Gz)/(Gz**2)
hbarc  = 0.197 * units.femto # GeV m
barn =  1e-28 # m^2
sigma_to_barn = (hbarc**2) / barn
print('sigma max (ee->mumu) {:3.1f} nbarns '.format(sigma_to_barn * sigma_mumu / units.nano))
print('sigma max (ee->had)  {:3.1f} nbarns '.format(sigma_to_barn * sigma_had /units.nano))
print('sigma max (ee->Z)    {:3.1f} nbarns '.format(sigma_to_barn * sigma_tot /units.nano))

sigma max (ee->mumu) 2.1 nbarns 
sigma max (ee->had)  41.6 nbarns 
sigma max (ee->Z)    60.2 nbarns 

def sigma(s, Gff = Gmm):
    return (12 * np.pi *s)/(mz**2) * (Gee*Gff/((s-mz**2)**2 + (mz*Gz)**2))
ss = np.linspace(mz-8, mz+8, 100)
plt.plot(ss, sigma_to_barn * sigma(ss*ss, Ghad) / units.nano); 
plt.grid(); plt.xlabel(r'$\sqrt{s}$ (GeV)'); plt.ylabel(r'$\sigma$ (nbarn)');
../_images/sm_39_0.png

5.4.3.2. Anchura de desintegración parcial#

Por otro lado, la anchura parcial de desintegración del \(Z \to f + \bar{f}\) viene dada por:

\[ \Gamma(Z \to f + \bar{f}) = \frac{g^2_Z m_Z}{24 \pi} (c^2_L + c^2_R) \]

Por ejemplo para \(\nu_e\) como \(c^{(\nu_e)}_L = 1/2, \; c^{(\nu_e)}_R = 0\):

\[ \Gamma (Z \to \nu_e + \bar{\nu}_e) = \frac{g^2_Z m_Z}{96 \pi} = 166 \; \mathrm{MeV} \]

Cuestión: Calcula las anchuras de desintegración parciales y totales de \(Z\) y sus fracciones de desintegración.

GF  = units.value("Fermi coupling constant")
s2t = units.value("weak mixing angle")
MW  = 80.34 # GeV 
MZ  = 91.19 # GeV
g2w = 8 * MW**2 * GF /np.sqrt(2)
g2z = g2w/(1-s2t) 
gamma_nu = g2z*MZ/(96*np.pi)
print('gw    {:5.4f}'.format(np.sqrt(g2w)))
print('gz    {:5.4f}'.format(np.sqrt(g2z)))
print('Gamma nue {:5.4f} GeV'.format(gamma_nu))

gw    0.6526
gz    0.7403
Gamma nue 0.1657 GeV

nc   = 3 # 3 colors for the quarks
pars = {'e':(-0.5+s2t, s2t), 'nue': (0.5, 0), 'u' : (0.5-2*s2t/3, -2*s2t/3), 'd': (-0.5+s2t/3, s2t/3)}
gamma = lambda cl, cr: g2z*MZ/(24*np.pi)*(cl**2 + cr**2)
gammas = {}
for key in pars.keys():
    cl, cr = pars[key]
    gammai = gamma(cl, cr)
    gammai = nc * gammai if key in ('u', 'd') else gammai
    comment = 'Gamma ' + key + ' {:5.4f} GeV'.format(gammai) 
    print(comment)
    gammas[key] = gammai

Gamma e 0.0838 GeV
Gamma nue 0.1657 GeV
Gamma u 0.2894 GeV
Gamma d 0.3713 GeV

La anchura total del \(Z \to f + \bar{f}\) es la suma de las parciales:

\[ \Gamma_Z = 3 \Gamma_{ll} + \Gamma_{\mathrm{had}} + N_\nu \Gamma_{\nu\nu} \]

donde \(\Gamma_{ll} = \Gamma_{ee} = \Gamma_{\mu\mu} = \Gamma_{\tau\tau}\) es la anchura de desintegración parcial a leptones cargados -que el modelo predice es la misma-, \(\Gamma_{\mathrm{had}}\) es la anchura de desintegración a hadrones (la total a \(q\bar{q}\)), y finalmente \(N_\nu\) es el número de neutrinos, y \(\Gamma_{\nu\nu}\) la anchura de desintegración a un neutrino de un solo sabor -el modelo también predice que es la misma para cada sabor de neutrinos-.

gamma_total = 3 * gammas['nue'] + 3 * gammas['e'] + 2 * gammas['u'] + 3 * gammas['d']
print('Total Gamma {:5.4f} GeV '.format(gamma_total))
for key in gammas.keys():
    #n  = 2 if key == 'u' else 3
    br = 100 * gammas[key]/gamma_total
    print('BR ' + key + ' {:3.1f} %'.format(br))

Total Gamma 2.4414 GeV 
BR e 3.4 %
BR nue 6.8 %
BR u 11.9 %
BR d 15.2 %

5.4.4. Tres familias de neutrinos#

A partir de la medidad de la sección eficaz en torno al \(Z\) podemos determinar experimentalmente de forma directamente \(m_Z, \Gamma_Z, \Gamma_{had}, \Gamma_{ll}\) y de forma indirecta el número de familias de neutrinos \(N_\nu\).

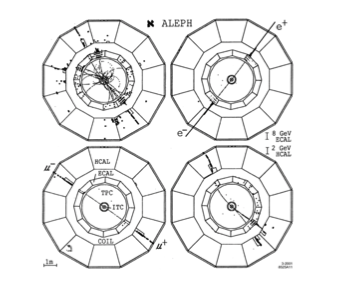
En la figura se muestra la vista transversal de varios eventos en ALEP: \(e+e^+ \to Z\) y \(Z \to\) hadrons, \(e+e^+, \mu+\mu^+, \tau+\tau^+\):

../_images/sm_Zevents_ALEPH.png

\(Z\to\) hadrons, \(e+e^+\), \(\mu+\mu^+\), \(\tau + \tau^+\) [ALEPH]

Como el momento transversal se conserva, observamos que el caso por ejemplo \(e+e^+ \to \mu+\mu^+\) los muones salen enfrentados. La signatura experimental es muy clara y diferente en cada uno de los casos.

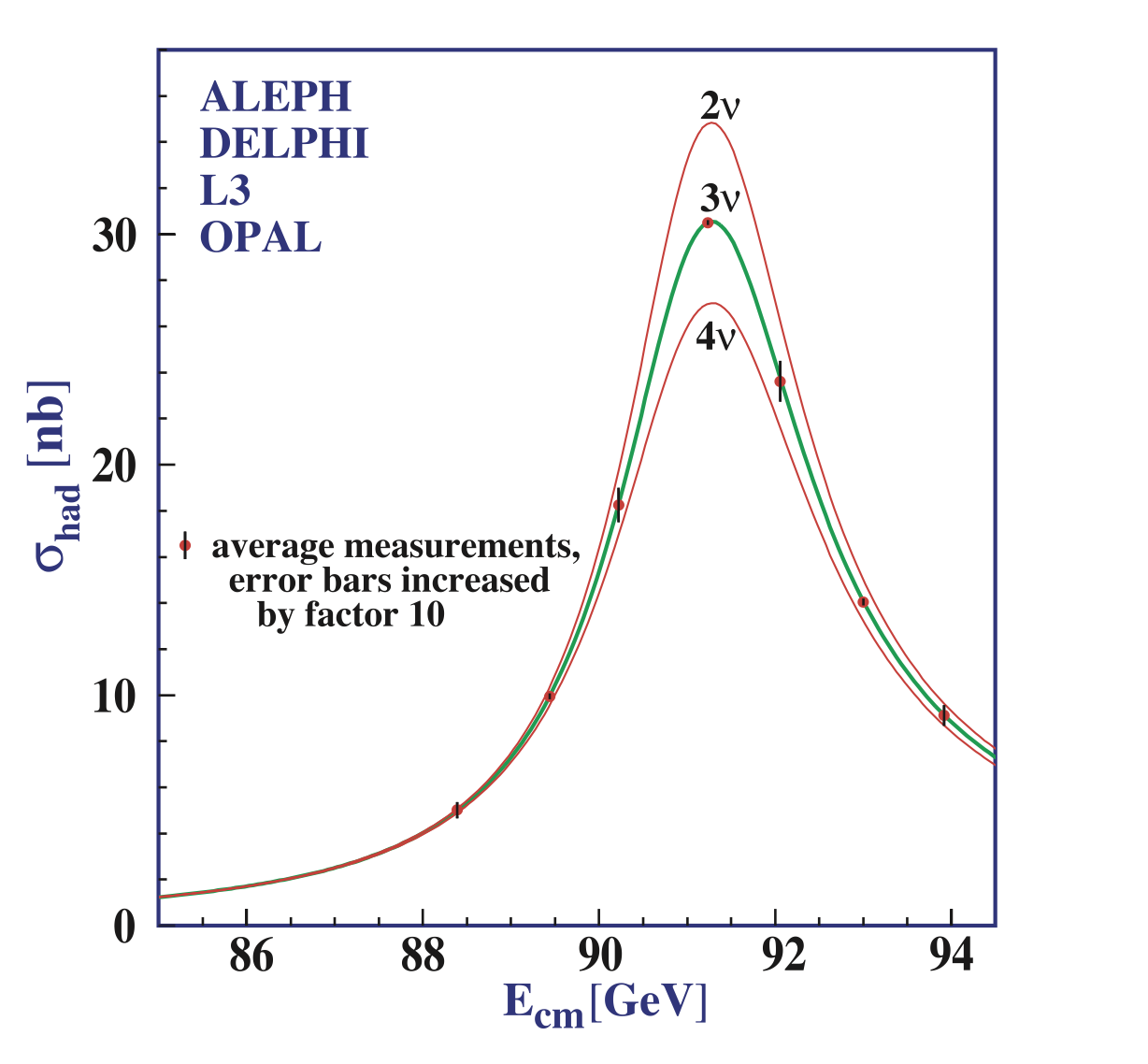
La siguiente figura muestra la sección eficaz \(\sigma(e+e^+ \to \mathrm{hadrons})\) en función de \(\sqrt{s}\) obtenida conjuntamente por los experimentos de LEP: ALEPH, DELPHI, L3 y OPAL.

../_images/sm_zresonance.png

\(\sigma(e+e^+ \to \mathrm{hadrons})\) vs \(\sqrt{s}\) de los experimentos de LEP [PDG]

Y en ella se muestra sobreimpuesta la línea con la predicción teórica para el caso de varios números de neutrinos (2, 3 y 4).

Hay que remarcar que los errores de los datos están dibujados cun un factor 10 de su valor real para que sean visibles en el dibujo.

A partir de los resultados experimentales, principalmente de LEP, se obtiene:

\(M_Z\)

\(91.1880 \pm 0.0020\) GeV

\(\Gamma_Z\)

\(2.4955\pm 0.0023\) GeV

\(\Gamma_{ll}\)

\(83.984 \pm 0.086\) MeV

\(\Gamma_{\mathrm{had}}\)

\(1744.4 \pm 2.0\) MeV

\(\Gamma_{\mu\mu}/\Gamma_{ee}\)

\(1.0001\pm0.0024\)

\(\Gamma_{\tau\tau}/\Gamma_{ee}\)

\(1.0020 \pm0.0032\)

Y podemos calcular el número de neutrinos.

Recordemos que el número de neutrinos, \(N_\nu\), entra en la anchura de desintegración como:

\[ \Gamma_Z = 3 \Gamma_{ll} + \Gamma_{\mathrm{had}} + N_\nu \, \Gamma_{\nu\nu} \]

A partir de la medida de \(\Gamma_Z = 2.4952 \pm 0.0023\), y de las anchuras medidas \(\Gamma_{ll} = 83.984 \pm 0.086\) MeV, \(\Gamma_{\mathrm{had}} = 1744.4 \pm 2.0\) MeV y del valor teórico de \(\Gamma_{\nu\nu} = 166 \, \mathrm{MeV}\), estimamos el número de neutrinos:

\[ N_\nu = 2.9840\pm 0.0082 \]

Esto es, existen solo tres familias de neutrinos.

Sin embargo, no sabemos por qué solo tres, ¡todo un misterio!

5.5. El bosón de Higgs#

El modelo de Higgs da respuesta (quizás la única posible) a los siguientes problemas graves que presentaba la teoría electro-debil.

  • Los bosones débiles son masivos, sin embargo las teorías gauge exigen bosones sin masa. ¿Cómo dotar entonces de masa a los bosones \(W^\pm, Z\)?

  • La teoría electrodébil separa fermiones a derechas e izquierdas, en dupletes y singletes, y exige que no tengan masas. ¡Pero sabemos que los fermiones tienen masa!

El mecanismo de Higgs permite dotar de masa a fermiones y bosones preservando la invariancia gauge de la teoría.

Es muy dificil esquivar el Lagrangiano del Modelo Estándar para hablar del Higgs.

Vamos a dar aquí solo unas ideas que nos permitan entender su comportamiento y descubrimiento.

5.5.1. Masa de los fermiones#

El término de masa asociado a los fermiones que aparece en el Lagrangiano es:

\[ m \bar{\Psi} \Psi \]

La masa es en principio una propiedad intrísica de la partícula, pero ¿qué si fuera la consecuencia de una interacción con un nuevo campo?

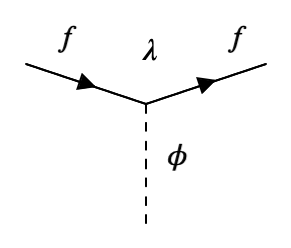
Supongamos que los fermiones se acoplan con un campo escalar \(\phi(x)\), cada ellos con un acoplo adimensional, \(\lambda\), -que llameremos de Yukawa-. El término de interacción en el lagrangiano será:

\[ \lambda \bar{\Psi} \Psi \phi \]

O gráficamente:

../_images/sm_higgs_2.png

Acoplo del campo de Higgs con el fermión

que corresponde a un vértice de tres ramas con un acoplo de Yukawa \(\lambda\).

Consideremos ahora un campo complejo escalar singular, \(\phi(x)\), con un valor mínimo, lo que llamamos un valor esperado en el vacío, \(v\), no nulo:

\[ \phi(x) = \frac{1}{\sqrt{2}}\left(v + h(x)\right) \]

(el factor \(1/\sqrt{2}\) simplifica luego los cálculos, pero no es relevante).

La interacción que hemos escrito anteriormente entre fermiones y el campo \(\phi\) queda:

\[ \lambda \bar{\Psi} \Psi \, \phi = \frac{\lambda v}{\sqrt{2}} \bar{\Psi} \Psi + \frac{\lambda}{\sqrt{2}} \bar{\Psi} \, \Psi h(x) \]

El primer término podemos asociarlo a la masa del fermión:

\[ m \bar{\Psi} \Psi = \frac{\lambda v}{\sqrt{2}} \bar{\Psi} \Psi \; \Rightarrow \; m= \frac{\lambda v}{\sqrt{2}}. \]

Podemos decir entonces que la masa aparece como la fricción, via el acoplo de Yukawa, \(\lambda\), con el valor esperado del campo escalar (de Higgs) en el vacío, \(v\).

El segundo término \(\bar{\Psi} \Psi h\) lo interpretamos como la interacción del campo \(h(x)\) con un fermión.

../_images/sm_higgs_0.png

Masa de los fermiones y la interacción con el higgs, \(h(x)\)

5.5.2. El campo del bosón de Higgs#

Hemos visto que podemos dotar de masa a los fermiones con un campo escalar, \(\phi(x)\), cuyo valor en el vacío, \(v\), sea no nulo, ¿pero cómo obtenemos ese valor \(v\)?

Consideremos un campo escalar complejo, que llamaremos campo de Higgs, su langrangiano es:

\[ (D_\mu \phi)^\dagger (D^\mu \phi) - m^2 \, (\phi^\dagger \phi), \]

Por cierto, notar que el lagrangiano presenta una simetría respecto a un cambio de fase \(\phi'(x) = e^{i \theta} \, \phi(x)\)

El segundo término del lagrangiano, el de masas, lo asociamos a un potencial.

\[ V(\phi) = m^2 \, (\phi^\dagger \phi) \]

que tienen una dependencia parabólica en términos de \((\phi^\dagger \phi)\).

Consideremos la extensión más sencilla de ese potencial, que sería cuadrática.

\[ V(\phi) = \frac{\mu^2}{2} (\phi^\dagger \phi) + \frac{\lambda}{4} (\phi^\dagger \phi)^2 \]

que depende de los parámetros \(\mu, \lambda\).

Notar que si \(\mu = \sqrt{2} m\) y \(\lambda = 0\), recuperamos el potencial inicial.

Los factores \(1/2, 1/4\) sirven para simplificar los cálculos, pero no son relevantes.

Las siguientes figuras muestran el potencial para los casos \(\mu^2>0, \mu^2<0\) con \(\lambda > 0\). Observa el valor \(v\), que corresponde al mínimo.

higgs_potential = lambda phi, mu, xlambda : ((mu**2).real * phi**2)/2 + (xlambda/4) * (phi**2)**2
phis = np.linspace(-10, 10, 100)
mu  = 6; xlambda = 1
plt.subplot(1, 2, 1); plt.plot(phis, higgs_potential(phis, mu, xlambda));
plt.subplot(1, 2, 2); plt.plot(phis, higgs_potential(phis, mu*(1j), xlambda));
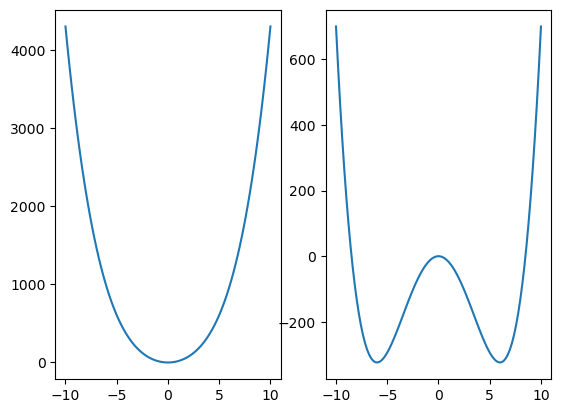
../_images/sm_59_0.png

El valor esperado del vacío, \(v\), es el estado de mínima energía:

  • El el caso \(\mu^2 >0\) el potencial tiene un mínimo en \(v = 0\).

  • Mientras que el caso \(\mu^2 <0\) tiene dos mínimos en:

\[ v = \pm \sqrt{\frac{-\mu^2}{\lambda}} \]

Nos referimos también a \(v\) como vev (por valor esperado en el vacío).

Para desarrollar el campo alredor del vev:

\[ \phi(x) = v + h(x), \]

debemos elegir un mínimo, esto es, ¡rompemos la simetría inicial!

Llamamos rotura espontánea de simetría al hecho de que aunque un sistema físico -esto es su lagrangiano-, tenga una simetría dada, el vacío -esto es el valor mínimo del campo- la rompe.

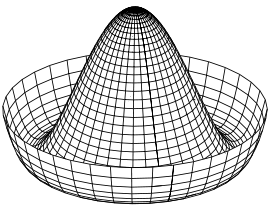
En el caso de que \(\phi\) sea un complejo obtenemos la curva del potencial conocida como sobrero mexicano, donde uno de los ejes es la componente real del campo y la otra la imaginaria:

../_images/sm_mexican_hat.png

potencial del campo complejo de Higgs \(V(\phi)\) [Wikipedia]

Luego la existencia de un campo escalar complejo, con un potencial tipo sombrero mexicano, nos permite obtener un valor esperado en el vacío, con el que dotar de masa a los fermiones y bosones vectoriales.

Pero, sin embargo, no tenemos un principio o una explicación de por qué este potencial. ¡Otro gran misterio!

El potencial de Higgs introduce dos parámetros libres (indeterminados), \(v\) y \(\lambda\) -o si se prefiere \(v\) y \(m_H\), el velor esperado en el vacío y la masa de Higgs-.

El mecanismo introduce además un parámetro adicional, el acoplo de Yukawa \(\lambda_f\), por cada fermión:

A cambio tras la rotura espontánea de simetría, el campo de Higgs da lugar:

  • a las masas de los fermiones (aunque no las predice, porque cada fermión tiene asociada una constante de Yukawa propia)

  • (aunque no lo vemos) a la masa de los besones vectoriales, \(m_W, m_Z\). En este caso predice el ratio entre las masas \(m_W\) y \(m_Z\).

  • su propia masa, \(m_H\), (aunque no la predice)

El modelo nos da un mecanismo para dotar de masas a los fermiones, pero no hace ninguna predicción sobre las mismas.

Pero sí predice:

  • que existen interacciones entre el higgs, \(h(x)\), y los bosones débiles, \(W, Z\), y dan lugar a las desintegraciones del Higgs a los bosones vectoriales

  • que las interacciones entre el higgs, \(h(x)\), y los fermiones, dan lugar a desintegraciones a pares fermión-antifermión

No solo eso, si no que el higgs se acopla también consigo mismo en vértices de tres y cuatro ramas, y con los bosones vectoriales débiles en vértices de cuatro ramas. Esto es, genera nuevas interacciones entre sí, y con los bosones vectoriales. En otras palabras, el Higgs presenta una física muy variada, en su mayor parte inexplorada todavía.

Por último, aunque no lo hemos desarrollado, el modelo estandar predice la masa del \(W^\pm\), \(m_W\)

\[ m_W = \frac{1}{2} g_W v \]

Por lo tanto, a partir de la medida de \(M_W\) y de \(g_W\) podemos determinar \(v\)

\[ v = \frac{2m_W}{g_W} = \sqrt{\frac{1}{\sqrt{2} G_F}} = 246 \; \mathrm{GeV} \]

esto es, \(v\) viene dado por la constante de Fermi, \(G_F\).

GF = units.value("Fermi coupling constant") # 1/GeV^2
v  = np.sqrt(1/(np.sqrt(2)*GF))
print('valor esperado del vacío {:4.1f} GeV'.format(v))

valor esperado del vacío 246.2 GeV

5.5.2.1. Las desintegraciones del bosón de Higgs#

El Higgs se acopla con los fermiones dependiendo de sus masas, a mayor masa, mayor acoplo. Esto va a determinar las posibles desintegraciones del Higgs.

Como el acoplo del Higgs es proporcional a la masa, aquellos canales permitidos con mayor masa son los favorecidos.

La siguiente tabla muestra las fracciones de desintegración para los distintos canales de un Higgs con una masa \(m_H = 125\) GeV

——— canal ——-

—– \(Br\) —–

\(H\to b + \bar{b}\)

57.8 %

\(H \to W^+ + W^-\)

21.6 %

\(H \to \tau + \tau^+\)

6.4 %

\(H \to g + g\)

8.6 %

\(H \to c + \bar{c}\)

2.9 %

\(H \to Z + Z^*\)

2.7 %

\(H \to \gamma + \gamma\)

0.2 %

Nota adicional Las desintegraciones \(H\to \gamma + \gamma, H \to g + g\) ocurren a través de diagramas de lazo, por ejemplo, con el intercambio en triángulo de un \(t\).

5.5.3. Descubrimiento del bosón de Higgs#

El bosón de Higgs se descubrió en 2012 en los experimentos ATLAS y CMS del LHC del CERN.

Con anterioridad los experimentos de LEP y los experimentos CDF y D0 de Fermilab habían constreñido el valor de su masa más ligera entre: \(115-150\) GeV.

Los experimentos y el acelerador LHC se diseñaron en los 80’s y entraron en operación a finales de los 2000’s.

En el LHC colisionan \(p+p\) a una energía \(\sqrt{s}= 7- 13\) TeV y con una luminosidad \(\mathcal{L}(t) = 10^{34} \; \mathrm{cm}^{-2}\). Hay \(10^{11}\) protones por paquete y una frecuencia de colisión de 40 MHz (cada 25 ns).

El número de colisiones \(10^{9}\) por segundo y por cada cruce hay como máximo \(35\) colisiones, lo que de denomila pile-up (apilamiento).

Las sección eficaz \(p+p\) is del ~100 mbars en el LHC.

Las sección eficaz medida de producción del \(H\) para \(\sqrt{s}=13\) TeV es 54 pbarns.

Los canales de desintegración dónde la señal es más fácil distinguible del fondo son \(H\to Z+Z^*\) y \(H \to \gamma \gamma\).

Eso equivale a buscar una desintegración relevante entre \(10^{13}\).

5.5.3.1. El descubrimiento del Higgs en ATLAS y CMS#

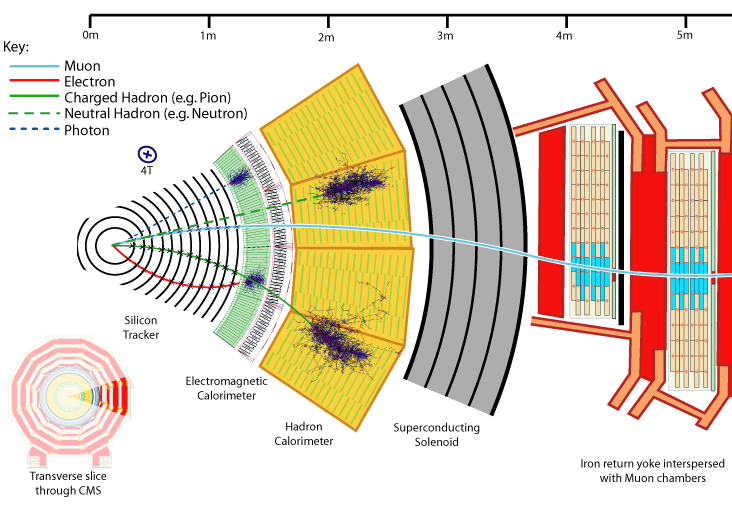
En la figura se muestra el esquema del experimento CMS del LHC:

../_images/det_CMS_subdetectors.png

Esquema de un sector del Compact Muon Selenoid (CMS) del LHC

El Higgs se descubrió en dos canales limpios (donde los sucesos de contaminación son o afectan menos).

  • \(H \to \gamma + \gamma\), buscando dos deposiciones en el calorímetro electromagnético, \(\gamma\).

mediante el cálculo de la masa invariante de los dos \(\gamma\), \(m_{\gamma\gamma}\), que provienen del punto de interacción.

  • En el canal \(H \to Z + Z^* \to (l+l^+) + (l'+l'^+)\), en cuatro leptones (\(4l\)), agrupados en dos parejas del mismo sabor y carga opuesta.

A partir de la masa invariante de los 4 leptones, \(m_{4l}\).

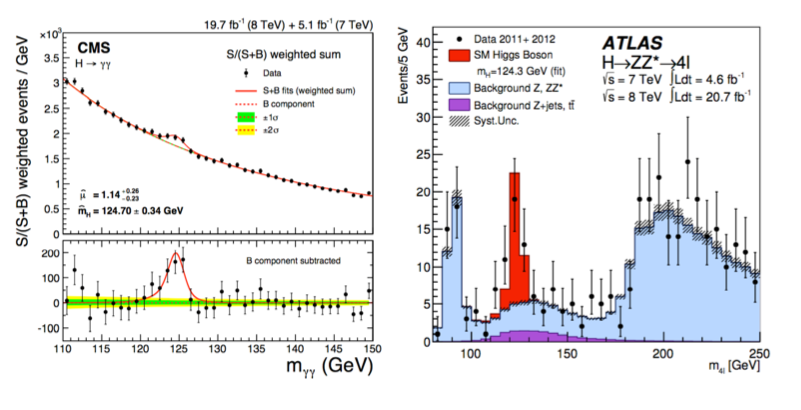
La siguiente figura muestra la presenta la distribución de la masa invariante de \(2 \gamma\) (izda) para el caso de CMS y de \((4 l)\) para el caso de ATLAS con la estadística de Run-I del LHC

../_images/sm_higgs_CMS_ATLAS.png

masa invariante para \(H \to \gamma \gamma\) (izda, [CMS]) y \(H \to Z+ Z^* \to 4 l\) (derecha, [ATLAS])

Observamos:

  • La presencia de un pico en la masa invariante en ambas distribuciones a 125 GeV.

  • Ese pico es incompatible con el fondo, en combinación a ~6 desviaciones estandars.

El valor esperimental de la masa del bosón de Higgs es \(m_H = 125.20 \pm 0.11\) GeV.

Con los datos del run-I del LHC se pudo concluir además:

  • que se trataba de una partícula escalar a partir de las distribuciones angulares de los \((4l)\) en el canal \(H\to 4 l\).

  • que el acoplo a otros canales \(\tau\tau^+, b \bar{b}\) es el esperado por el SM

En la figura dos eventos de ATLAS, identificados como \(H \to \gamma\gamma\) (izda) y \(H \to e+e^++\mu+\mu^+\)

../_images/sm_atlas_h2gammas_event.png

../_images/sm_atlas_h4leptons_event.png

\(H \to \gamma + \gamma\) event

\(H \to 4l\) event ATLAS events

5.6. Conclusions#

El SM:

  • El SM clasifica las partículas conocidas y describe con precisión las interacciones electrodébiles y fuertes entre ellas.

  • El SM se ha verificado en numerosos procesos físicos y experimentos.

  • No obstante sabemos que los neutrinos tienen masa, lo que implica que debemos extender el SM.

Pero:

  • No incluye otra Física conocida, como la materia oscura, ¿qué partículas la forman?

  • El modelo tiene cinco parámetros fundamentales \(e, g_W, g_S, v, \lambda\), dos de ellos corresponden al Higgs. Experimentalmente \(\alpha, G_L, \alpha_S, M_Z, M_H\).

  • Tiene 9 parámetros adicionales, que son los acoplos de Yukawa (las masas de los leptones cargados y de los quarks); 4 más para acomodar la matriz CKM de los quarks, y 4 más para la PNMS de los leptones (la que rige las ocilaciones de neutrinos).

5.6.1. cuestiones abiertas#

  • ¿Es el neutrino su propia antipartícula? ¿Cómo se acopla al Higgs?

  • ¿Cuál es el origen de los valores de masas? ¿Por qué es tan pequeña la masa del neutrino?

  • ¿Por qué hay 3 familias? ¿Qué relación guardan, si la hay, la matriz CKM y PNMS?

  • ¿Es el Higgs único? ¿Es el Higgs compuesto?

  • ¿Cuál es el origen del potencial del bosón de Higgs, \(V(\phi)\)?

  • ¿Hasta qué escala de energía, \(\Lambda\), es válido el SM? ¿A qué energía aparecerá nueva física?

5.7. Bibliografía#

  • [MT] Mark Tomsom, «Modern Particle Physics», Cambridge U. press, Temas 15, 16 y 17.

  • [AB] Alessandro Bettini, «Introduction to Elementary Particle Physcs», Cambridge U. press, Tema 9.

  • [PK] M. Peskik, Lectures on the Theory of the Weak Interaction, SLAC–PUB–17142, (2017), arXiv:1708.0943v1

  • PDG Particle Data Group.

  • [LEP-SLD] LEP and SLD Collaborations. 2006. Phys. Rept., 427, 257–454.

  • [DELPHI] P. Abreu et al., DELPHI Collaboration, Eur. Phys. J. C 11, 383 (1999).

  • [ALEPH] D. Decamp et al., ALEPH Collaboration, Z. Phys. C 48, 365 (1990)

  • [CMS] V. Khachatryan et al., CMS Collaboration, Eur. Phys. J. C 74, no. 10, 3076 (2014) arXiv:1407.0558

  • [ATLAS] G. Aad et al., ATLAS Collaboration, Phys. Lett. B 726, 88 (2013) Erratum: [Phys. Lett. B 734, 406 (2014)] arXiv:1307.1427