Extensión: grupos
Contents
9. Extensión: grupos#
import time
print(' Last version ', time.asctime() )
Last version Mon Dec 2 15:30:43 2024
9.1. Introducción#
En esta extensión vamos a revisar los conceptos de grupo, representación fundamentl e irreducible. Recordaremos todos ellos con un ejemplo conocido de la mecánica cuántica: es espín \(s=1/2\).
Luego definiremos los grupos principales y nombraremos su uso principal en Física de Partículas.
Grupo \(U(1)\) y \(SO(2)\). La carga eléctrica.
Grupo \(SU(2)\) y \(SO(3)\). El isoespín débil.
Grupo \(SU(3)\). El isoespín de sabor y de color.
9.2. sobre los grupos#
Los grupos de simetría son una de las herramientas matemáticas principales de la Física de Partículas:
están relacionadas con las cantidades conservadas, por ejemplo con las cargas que definen una partícula.
sirven para representar los estados de las partículas. En este sentido usamos las bases de las representaciones irreducibles para representar los estados de las partículas.
Vamos a recordar el concepto de grupo, de representación, y después revisaremos los grupos principales \(U(1), SU(2)\) y \(SU(3)\).
Los grupos más comunes en física de partículas son:
El grupo de Lorentz-Poincaré, asociado a las rotaciones, traslaciones y cambios de sistemas de referencia inerciales en el espacio-tiempo.
Las representaciones más comunes que encontramos son: escalar, vectorial, espinorial
Par la discusión sobre el grupo y las representación de Lorentz ver extensión [ext-trans-Lorentz].
Los grupos unitarios (cuya representación son matrices unitarias) de dimensiones pequeñas:
U(1) rotación de una fase de un número complejo, que asociamos con la conservación de la carga eléctrica.
SU(2) matrices unitarias de dimensión 2 con determinante positivo, que asociamos al espín, y a otras contidades físicas como el isoespín débil. Su base fundamental es un duplete con posiciones arriba y abajo.
SU(3) matrices unitarias de dimensión 3 con determinante positivo, que asociamos al color. Su base fundamental es un triplete, que asociamos en el caso del color con los tres colores: rojo, verde y azul.
9.2.1. Definión de grupo#
Un grupo es una colección de elementos, \(\{g_i\}\), finito o infinito entre los que hay definida una operación, la multiplicación (\(\cdot\)), y que cumple las siguientre propiedades:
completitud: \(g_i \cdot g_j = g_k\) (la multiplicación de dos elementos del grupo da otro elemento del grupo)
asociación: \(g_i \cdot (g_j \cdot g_k) = (g_i \cdot g_j) \cdot g_k\)
existencia de la identidad, \(1\): \( g_i \cdot 1 = 1 \cdot g_i = g_i\)
existencia de la inversa, \(g_i \cdot g^{-1}_i = 1\) para todo \(g_i\) del grupo.
Decimos que el grupo es abeliano si es conmutativo: \(g_i \cdot g_j = g_j \cdot g_i\), si no, es no-abeliano
9.2.1.1. Clasificación de grupos#
Los grupos principales son:
espacio-temporales, lo que incluye el grupo de Lorentz
de un espacio interno, llamado isotópico, que pueden ser globales o locales (esto es que depende del punto espacio-temporal).
Tambien se pueden clasificar los grupos en:
continuos, si el grupo depende de un parámetro \(\theta\) continuo, que puede ser compacto o no dependiendo si el intervalo del valor que toma \(\theta\) es abierto o cerrado. Por ejemplo el grupo de Lorentz que depende del parámetro \(\beta = v/c\) no es compacto porque no puede tomar el valor \(\beta = 1\).
discretos, donde hay un grupo finito de elementos. Por ejemplo la inversión por paridad forma un grupo discreto de un elemento.
En Física de Partículas juegan un papel fundamental los grupos de Lie que son aquellos cuya elementos se relacionan de forma continua y diferenciable con respecto a un conjunto de parámetros \(\theta\).
9.2.2. Representaciones#
Llamamos representación líneal \(D(g)\) al conjunto de matrices asociadas con los elementos \(g\) de un grupo \(G\) que cumplen las mismas reglas de multiplicación que los elementos de \(G\).
Esto es:
La dimensión de la representación, \(n\), es la dimensión de las matrices.
Los vectores de dimensión \(n\) sobre los que actuan las matrices forman la base de la representación.
Llamamos representación fundamental aquella representación del grupo con la dimensión menor.
9.2.2.1. Representación irreducible#
Decimos que una representación \(D(g)\) de un grupo \(G\) es reducible si puede descomponerse en representaciones más pequeñas.
Sea la representación \(D(g)\) de matrices de dimensión \(n\times n\) de un grupo, la representación es redudible si la matrix \(D(g)\) se puede descomponer en diagonal con matrices de menor dimensión, \(D_1(g), D_2(g)\), de la forma:
También podemos decir que la base de la representación \(D(g)\) se puede descomponer en varias bases, de tal forma que los elementos de cada sub-base forman su propio grupo. Esto es, los elementos de la base \(D_1(g)\) no se mezclan con los elementos de la base de \(D_2(g)\).
Como dijimos antes los estados de las partículas se representan en las bases de la representación irreducible.
9.2.3. Ejemplo: el espín#
El conjunto de matrices complejas unitarias don determinante unidad (esto es propias) forman el grupo \(SU(2)\).
El álgebra de este grupo es igual a la del momento angular, y usamos este grupo para representar el espín de los fermiones \(s = 1/2\), que contiene dos estados en su base fundamental, el duplete:
Los generadores del grupo son los operadores proyección de espín en las coordemadas \(x, y, z\): $\( S^i = \frac{1}{2} \sigma^i \)\( donde \)\sigma^i$ son las matrices de Pauli.
que cumplen la siguiente álgebra $\( [S^i, S^j] = \epsilon_{ijk} S^k \)\( donde \)\epsilon_{ijk}$ es el tensor de Levi-Civita. Esta es el álgebra del momento angular.
Las matrices del grupo \(SU(2)\) se construyen a partir de los generadores mediante exponenciación y su desarrollo de Taylor. $\( U(\theta) = e^{i\vec{\theta} \cdot {\bf S}} = e^{i \theta_i S^i} \)\( donde \)\theta_i\( son tres ángulos de rotación alrededor de los ejes \)x, y, z$.
Por ejemplo la rotación de un ángulo \(\theta\) alrededor del eje \(y\) queda: $\( U(\theta) = e ^{i \theta S^2} = \sum_n \frac{1}{n!}(i\theta S^2)^n = 1 + i \theta S^2 - \frac{1}{2} \theta^2 (S^2)^2 + \dots \)$
dado que \((\sigma^2)^2 = I\) obtenemos
Recordemos que dado que \(U\) es unitaria los generadores, \(S^i\), son hermíticos y por lo tanto tienen asociados valores observables.
Los tres generadores, \(S^i\) no conmutan entre sí. Pero el operador momento total al cuadrado $\( {\bf S}^2 = (S^1)^2 + (S^2)^2 + (S^3)^2 \)\( conmuta con \)S^3\(, esto es: \)\( [{\bf S}^2, S^3] = 0. \)$
De tal forma que damos los estados a partir de los números cuánticos de ambos operadores, como \(|j, m \rangle\), donde \(j\) es el momento angular total y \(m\) la tercera componente, así:
Y hacemos la asociación:
El producto de dos spines \(s=1/2\), dos dupletes, que se denota por \({\bf 2} \otimes {\bf 2}\), nos da las siguientes combinaciones: $\( \uparrow\uparrow, \, \uparrow\downarrow, \, \downarrow\uparrow, \, \downarrow\downarrow \)$.
La representación del la composición \({\bf 2} \otimes {\bf 2}\) tiene dimensión 4. Su representación irreducible está formada por un triplete y un singlete, que se denota como \({\bf 3} \oplus {\bf 1}\).
El triplete es: $\( |1, 1 \rangle = \; \uparrow\uparrow, \;\;\; |1, 0 \rangle = \frac{1}{\sqrt{2}} (\uparrow\downarrow + \downarrow\uparrow), \;\;\; |1, -1 \rangle, = \; \downarrow\downarrow, \)\( y el singlete: \)\( |0, 0 \rangle = \frac{1}{\sqrt{2}}(\uparrow\downarrow - \downarrow\uparrow) \)$
Que asociamos con los estados, \(|j, m\rangle\), donde \(j = 1\) y \(m = 1, 0, -1\), y \(j = 0, m=0\)
para construir la representación irreducible usamos los operadores escalera:
que en la representación fundamental son simplemente: $\( S^+ = \sigma^+ = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}, \;\;\; S^- = \sigma^- = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}. \)$
El producto \({\bf 2} \otimes {\bf 2}\) se construye a partir por ejemplo del estado \(\uparrow\uparrow\) y el operador \(S^{-1}\)
Que si normalizamos: $\( |1, 1 \rangle = \uparrow\uparrow, \;\; |1, 0 \rangle = \frac{1}{\sqrt{2}} (\uparrow\downarrow + \downarrow\uparrow), \;\; |1, -1 \rangle = \downarrow\downarrow. \)$
y finalmente, el miembro del singlete, \(|0, 0 \rangle\), es el ortogonal a \(|1, 0 \rangle\):
Los miembros del triplete son simétricos bajo el intercambio \(\uparrow \leftrightarrow \downarrow\) y el singlete anti-simétrico.
De forma genérica para el producto de dos representaciones \(|j_1, m_1 \rangle |j_2, m_2 \rangle\), las representaciones irreducibles vienen dadas por:
\(j = |j_1 - j_2|, \, |j_1 - j_2| + 1, \dots, \, j_1+j_2, \, j_1+j_2\)
\(m = -j, -j+1, \dots, j-1, j\).
Para obtener la base \(|j, m \rangle\), usamos los operadores escalera, \(J^+, J^-\), que recordemos actuan de la siguiente forma: $\( J^+ \, |j, m \rangle = \sqrt{j (j+1) - m (m+1)} \, |j, m \rangle \\ J^- \, |j, m \rangle = \sqrt{j (j+1) - m (m-1)} \, |j, m \rangle \)$ esto es, suben arriba y abajo en los elementos de la base.
Recordemos finalmente que los coeficientes de Clebsch-Gordan nos relacionan los elementos de la base \(|j, m \rangle\) con los iniciales \(|j_1, m_1 \rangle |j_2, m_2 \rangle\).
Para construir las matrices unitarias de una representación irreducible obtenemos primero sus generadores a partir de los operadores escalera.
Para \(j=1\) los operadores escalera, cuyos coeficientes pueden obtenerse de las reglas de operación anteriores, son:
El generador de la rotaciones, \(J^2\), para \(j=1\) alrededor del eje \(y\), viene dado por: $\( J^2 = - \frac{i}{2} (J^+ - J^-), \;\; J^2 = -\frac{i}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 1 \\ 0 & -1 & 0\end{pmatrix} \)$
De tal forma que la matriz de rotación de un ángulo \(\theta\) alrededor del eje \(y\) para \(j=1\) viene dada por: $\( U(\theta) = e^{i \theta J^2} = \sum_n \frac{1}{n!} (i \theta J^2)^n = \begin{pmatrix} \frac{1}{2} (1+\cos \theta) & \frac{1}{\sqrt{2}} \sin \theta &\frac{1}{2}(1-\cos \theta) \\ -\frac{1}{\sqrt{2}} \sin \theta & \cos \theta & \frac{1}{\sqrt{2}}\sin \theta \\ \frac{1}{2} (1-\cos \theta) & -\frac{1}{\sqrt{2}} \sin \theta &\frac{1}{2}(1+\cos \theta) \\ \end{pmatrix} \)$
Los valores \(d^j_{m', m}(\theta)\) de las configuraciones de \(j\) menores se recogen en la tabla del PDG de los Clebsch-Gordan, a partir de ellos podemos reconstruir las matrices de rotación para la representación \(j\).
9.3. El grupo \(U(1)\)#
El grupo \(U(1)\) lo forman las rotaciones, \(D(\theta)\), de 1 dimensión en el espacio complejo.
Consideremos un número complejo, \(x\), relacionado con otro número complejo, \(x'\), simplemente por una fase \(x' = e^{i\theta} x\). La rotación entre ellos es:
Estas rotaciones dejan invariante la norma: $\( |x'|^2 = |x| \)$
La multiplicación de los elementos del grupo es:
Nos dice que es un grupo abeliano. No importa el orden en que se realizan dos rotaciones. Esto es el orden de multiplicación.
La inversa es simplemente:
La representación fundamental tienen demisión 1. Y el generador de las rotaciones es también la unidad.
9.3.1. El grupo \(SO(2)\)#
El grupo \(SO(2)\) está formado por matrices de las rotaciones, \(R(\theta)\), propias en dos dimensiones, \(R(\theta)\). Recordemos que las matrices propias tiene el determinante positivo.
Sea \((x, y)\) un punto del espacio bi-dimensional, el efecto de una rotación es:
Donde $\( R(\theta) = \begin{pmatrix} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{pmatrix}, \;\;\; \mathrm{det}(D(\theta)) = 1 \)$
El grupo SO(2) es continuo y compacto, con \(\theta \in [0, 2 \pi]\).
Las rotaciones preservan el modulo del vector:
Las reglas de multiplicación de las matrices \(R(\theta)\) son:
Si hacemos una rotación de \(\theta_2\) después de hacer una rotación previa de \(\theta_1\) es equivalente a rotar desde el principio con \(\theta_1+\theta_2\)
Se trata de un grupo abeliano, \(D(\theta_1) \cdot D(\theta_2) = D(\theta_2) \cdot D(\theta_1)\)
La inversa de una rotación con \(\theta\) es simplemente rotar con \(-\theta\): $\( R^{-1}(\theta) = R(-\theta) \)$
En la representación matricial \(2\times2\), la inversa es la transpuesta:
El generador de la rotaciones es:
De tal forma que: $$ R(\theta) = e ^{i \theta T} = \sum_n \frac{(i\theta T)^n}{n!} =
$$
Las reglas de multiplicación del grupo \(SO(2)\) y \(U(1)\) son las mismas:
Decimos que dos grupos son isomorfos si comparten las mismas reglas de multiplicación.
En este caso decimos que SO(2) y U(1) son isomorfos.
La base de uno y otro se relacionan por:
9.3.2. la carga eléctrica#
El grupo \(U(1)\) lo utilizamos en Física de Partículas para dar la invariancia gauge local de los espinores de Dirac frente al cambio de una fase global (lo que asociaremos con la conservación de números cuánticos como el número leptónico) o local (lo que asociaremos con la conservación de la carga eléctrica y que dará lugar a la interacción de los fermiones cargados con el campo electromagnético)
El grupo \(U(1)\) global respecto a los espinores de Dirac: $\( \Psi(x) \to e^{i \theta} \Psi(x) \)$
Y el grupo \(U(1)\) local: $\( \Psi(x) \to e^{i \theta(x)} \Psi(x) \)\( donde \)\theta(x)\( depende de forma continua y *local* con respecto al punto espacio-temporal \)x$.
9.4. El grupo \(SU(2)\)#
El grupo \(SU(2)\) lo forman las matrices complejas unitarias \(2 \times 2\) con determinante unidad. \(S\) es por propias, con determinante unidad, \(U\) por complejas unitarias y \(2\) corresponde a la dimensión.
Las matrices cumplen: $\( U^\dagger U = I, \;\; \mathrm{det}(U) = 1 \)$
Sea un vector de dos componentes complejas \({\bf x} = (x, y)\), la matrices lo transforman es: $\( {\bf x}' = U \, {\bf x} \)\( y conservarn el módulo del vector: \)\( |{\bf x}'|^2 = |{\bf x}|^2 \)$
Las matrices, \(U(\theta)\) pueden construirse a partir de los ángulos \(\theta_i\) y 3 generadores hermíticos \(T_i\), con \(i=1, 2, 3\): $\( U({\bf \theta}) = e^{i \vec{\theta }\cdot {\bf T}} = e^{i \sum_i \theta_i T^i} \)$
Los generadores \(T^i\) son: $\( T^i = \frac{1}{2} \sigma^i \)\( y \)\sigma^i\( las matrices de Pauli. Cumplen las siguiente álgebra de conmutación: \)\( [T^i, T^j] = i \epsilon_{ijk} T^k, \)\( donde \)\epsilon_{ijk}$ es el tensor de Levi-Civita.
Los elementos de la base los damos a partir de los números cuánticos de los operadores \({\bf T}^2, T^3\), dados por \(|j, m \rangle\). Donde:
La representación fundamental, \(j=1/2\), es: $$
$$
La discusión sobre composición de estados y representaciones irreducibles is idéntica a las del espín (ver arriba)
9.4.1. El grupo \(SO(2)\)#
El grupo \(SO(3)\) lo forman las matrices ortogonales, \(R\), de determinante positivo que corresponden a las rotaciones en el espacio vectorial de tres dimensiones. La \(O\) del nombre del grupo indica que son ortogonales.
Las rotaciones nos dejan invariante la norma del vector \({\bf x} = (x, y, z)\).
Las matrices, \(R(\theta)\), quedan definidas con tres ángulos, \(\theta_i\), con \(i=1, 2, 3\), a través de tres generadores hermíticos: $\( R(\theta) = e^{i \vec{\theta} \cdot T} = e^{i \sum_i \theta_i T^i} \)\( donde: \)\( T^1 = -i \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0\end{pmatrix}, \;\; T^2 = -i \begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0\end{pmatrix}, \;\; T^3 = -i \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}. \)$
Que cumplen la siguiente algebra de conmutación: $\( [T^i, T^j] = i \, \epsilon_{ijk} \, T^k \)\( donde \)\epsilon_{ijk}$ es el tensor Levi-Civita.
Estas son nuevamente las reglas de conmutación del momento angular y del grupo \(SU(2)\).
Como comparten la misma álgebra decimos que grupo \(SU(2)\) es isomorfo a \(SO(3)\)
La relación entre los elementos de cada grupo es:
9.4.2. El isoespín de sabor#
El quark \(u\) y el quark \(d\) se diferencian principalmente por su carga, dado que tienen masas muy similares. La fuerza fuerte sin embargo no hace distinción entre ellos, no distingue el sabor de los quarks.
Podemos definir entonces un isoespín de sabor y asociar cada uno de los quarks con los elementos de la base fundamental del \(SU(2)\), (o \({\bf 2})\). La fuerza fuerte debe ser invariante respecto una tranformación unitaria entre ambos.
Igualmente podemos asociar también los antiquarks a la representación fundamental \({\bf \bar{2}} \)
De tal forma que los mesones ligeros podemos asociarlos a los elementos de las representaciones irreducibles de un par quark-antiquark \({\bf 2} \otimes {\bf \bar{2}}\) y los bariones ligeros a tres quarks \({\bf 2} \otimes {\bf 2} \otimes {\bf 2}\)
9.4.3. El isoespín débil#
Para las interacciones débiles definimos un isoespín débil asociando el espinor a izquierdas de leptón cargado y del neutrino de su sabor con los elementos de un duplete de \(SU(2)\), y de igual forma hacemos con el espinor a izquierdas de quark de abajo y arriba:
Por ejemplo para la primera generación de leptones y quarks, tendríamos los dupletes $\( L \equiv \begin{pmatrix} \nu_e|_L \\ e_L \end{pmatrix}, \;\; Q \equiv \begin{pmatrix} u_L \\ d_L \end{pmatrix}, \)$
y exegimos que el lagrangiano débil sea invariante bajo rotaciones locales en el espacio de isoespín débil
donde \(\theta_i(x)\) son funciones continuas y locales del punto espacio-temporal
9.5. El grupo SU(3)#
Las matrices unitarias \(3 \times 3\) con determinante unidad forman el grupo \(SU(3)\).
Las matrices, \(U\), cumplen: $\( U^\dagger U = I, \;\; \mathrm{det}(U) = 1 \)$
Un vector complejo \({\bf x} = (x, y, z)\) mantiene la norma bajo transformacion del grupo \(SU(3)\).
El número de parámetros reales libres de SU(3) es 8. Hay \(18 = 3 \times 3 \times 2\) parámetros reales en \(U\), 9 ligaduras de la condición de unitariedad y 1 por ser el determinante unidad.
Las matrices de SU(3) pueden construirse a partir 8 generadores hemíticos, \(T_i\), y \(\theta_i\) con \(i = 1, \dots, 8\)
Las matrices \(U(\theta)\) de \(SU(3)\) se contruyen con 8 ángulos, \(\theta_i\) y 8 generadores hermíticos, \(T^i\),
El número de parámetros reales libres de SU(3) es 8. Hay \(18 = 3 \times 3 \times 2\) parámetros reales en \(U\), 9 ligaduras de la condición de unitariedad y 1 por ser el determinante unidad.
Una opción conveniente para los generadores es construirlos a partir de las matrices \(\lambda\) de Gell-Mann.
Donde:
Solo tres de los generadores conmutan entre ellos, \({\bf T}^2, T_3, Y_8\).
Podemos escribir un elemento del grupo con los números cuánticos \(|j, m, y \rangle\). En la representación fundamental:
Los números cuánticos ahora serán \(m\), tercera componente del isoespín, asociada a \(T^3\), e \(y\) a la hypercarga, a \(Y_8\).
Los elementos de la representación fundamental en función del la tercera componente y de la hypercarga quedan:
9.5.1. simetría \(SU(3)\) de sabor.#
Aún podemos considerar que los tres quarks ligeros, de masas parecidas, se diferencian sólo por su sabor y su carga.
Pero la fuerza fuerte es insensible al sabor. Por lo que podemos asociar dada uno de los quarks ligeros, \(u, d, s\) a los elementos de un triplete de \(SU(3)\). De tal forma que la fuerza fuerte sea invariante frente a transformaciones unitarias de los tres.
De esta forma nuevamente, la combinación de un par quark, anti-quark, \({\bf 3} \otimes {\bf \bar{3}}\) y de tres quarks \({\bf 3} \otimes {\bf 3} \otimes {\bf 3}\) nos permite obtener la composición de los mesones y los bariones ligeros.
9.5.2. El color#
La fuerza fuerza establece que tenemos tres colores, rojo, verde y azúl, \(r, g, b\), que podemos asociar a un triplete de \(SU(3)\). En el Modelo Estándar se exige que la fuerza fuerte sea invariante bajo transformaciones unitarias locales del color.
Los tres colores son los elementos del triplete:
Esta invariancia gauge local nos dará lugar a la cromodinámica cuántica (QCD).
También nos permite dar las composición de sabor de los mesones y bariones. Exigiremos que los hadrones sean incoloros, es decir que sus números cuánticos (tercera componente y hypercarga) de sabor sean nulos.
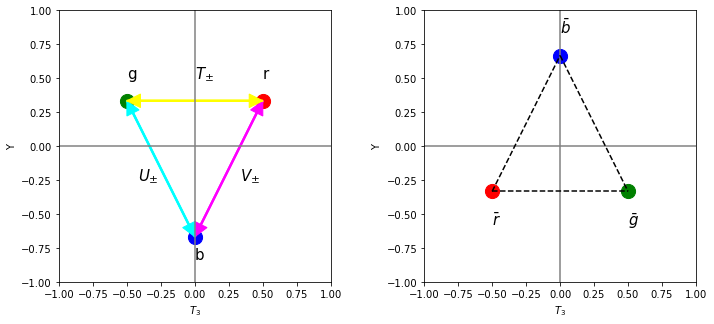
La figura muestra los dos tripletes de color \({\bf 3}\) de los quarks y anti-quarks \({\bf \bar{3}}\) en el plano \(T_3, Y\). Notar la oposición de cargas para los elementos de la representación \({\bf \bar{3}}\).
Posición de \(r, g, b\) en \((T_3, Y)\), \({\bf 3}\), y la dirección de los operadores \(T_\pm, V_\pm, U_\pm\) (izda) y de los \(\bar{r}, \bar{g}, \bar{b}\), \({\bf \bar{3}}\), (derecha) |
Existen ahora tres operadores escalera: $\( T_{\pm} = \frac{1}{2}(\lambda_1 \pm i \lambda_2), \; V_{\pm} = \frac{1}{2} (\lambda_4 \pm i \lambda_5), \; U_{\pm} = \frac{1}{2}(\lambda_6 \pm 9 \lambda_7) \)$
que suben y bajan los spinores a lo largo de la direcciones del triángulo (ver figura):
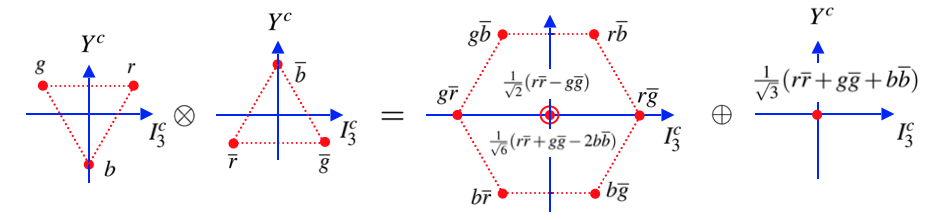
La combinación de los colores de quark y antiquark (mesón), \({\bf 3} \otimes {\bf \bar{3}}\), se efectua colocando el triplete \({\bf \bar{3}}\) sobre los vértices del \({\bf 3}\). Lo que da lugar a un octete y un singlete en su representación irreducible.
Combinación \({\bf 3} \otimes {\bf \bar{3}} = {\bf 8} \oplus {\bf 1}\) [MT] |
El único singlete tiene \(T_3 = , Y = 0\), esto es es incoloro, viene dado por:
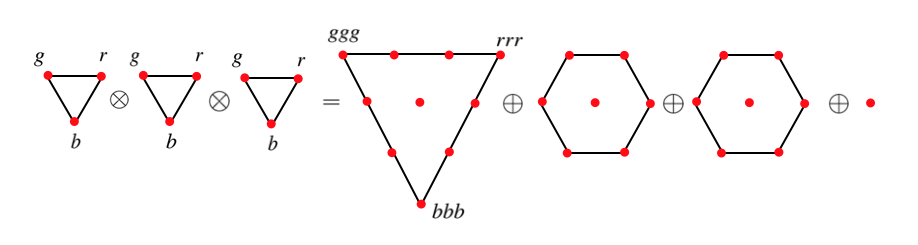
La combinación de dos quarks, \({\bf 3} \otimes {\bf 3}\), no da un singlete de color pero sí la de tres quarks, \({\bf 3} \otimes {\bf 3} \otimes {\bf 3}\) (ver figura).
Combinación \({\bf 3} \otimes {\bf 3} \otimes {\bf 3} = {\bf 10} \oplus {\bf 8} \otimes {\bf 8} \otimes {\bf 1}\) [MT] |
El singlete, con \(T_3 = 0, Y = 0\), este es sin color, viene dado por: