Extensión: La ecuación de Dirac
Contents
7. Extensión: La ecuación de Dirac#
import time
print(' Last version ', time.asctime() )
Last version Mon Sep 29 15:09:06 2025
7.1. Introducción#
En la presente extensión vamos a introducir con cierto detalle la ecuación de Dirac, los espinores de Dirac de fermiones y antifermiones, así como los conceptos fundamentales de espín, helicidad y chiralidad. También introduciremos el espinor adjunto y la corriente fermónica. Introduciremos también las otras formas bilineales.
Todos ellos son conceptos fundamentales en Física de Partículas.
Por otro lado la relación entre los espinores de Dirac y las transformación de Lorentz, boost y rotaciónes, así como también la inversión por paridad y carga, se tratan en las extensiones de [ext-trans-Lorentz].
7.2. Sobre la ecuación de Dirac#
Dirac propuso en los años 30 del siglo XX una ecuación que describe la dinámica de los fermiones libres.
Construyó su ecuación de tal forma que fuera invariente Lorentz, apareciesen linealmente los operadores de energía y momento de la mecánica cuántica, \(\hat{E} = i \partial_0, \; \hat{p} = -i \nabla\), y que contuviese implícitamente la ecuación de Einstein, \(E = m^2 + p^2\).
La solución de la ecuación de dirac, \(\Psi(x)\), es un nuevo tipo de objeto físico, un espinor, que describe los fermiones libres, partículas con un momento angular intrínseco o espín de \(1/2\). \(\Psi(x)\) no es sólo una función de ondas, si no cuatro, puestas en forma de columna. Este nuevo objeto se transformará con una reglas específicas bajo transformaciones Lorentz, que veremos, se derivan de la invariancia Lorentz de la propia ecuación de Dirac. En particular un espinor bajo rotaciones regresa a a su forma original tras girar dos veces, \(4\pi\), esto es, un giro le afecta «la mitad», de ahí que su espín sea 1/2.
Dos de las soluciones de Dirac tenían energía negativa. Dirac mismo propuso una interpretación muy iluminadora de su significado, indicando que las soluciones de energía negativa se correspondían con anti-partículas. Anti-partícula sería la ausencia de partícula, y por lo tanto tendría sus cargas opuestas. El descubrimiento del positrón supuso el espaldarazo de la existencia de las anti-partículas y de la ecuación de Dirac.
Las cuatro soluciones indenpendientes de Dirac corresponden a un fermión y sus dos componentes de espín, por ejemplo el electrón con carga \(-e\), y al anti-fermión, por ejemplo, el positrón, que tiene la cargas opuesta, \(+e\), y sus dos componentes de espín. La ecuación de Dirac introduce de forma natural el espín, el momento angular intrínsico de una partícula, y a las antipartículas. ¡Todo un logro!
En la ecuación aparecen ademas cuatro matrices, \(\gamma^\mu\) con \(\mu = 0, 1, 2, 3\), iguales en todos los sistemas inerciales, que aunque admiten diversas representaciones, cumplen unas reglas de conmutación que permiten como un engranaje, al asociarlas al momento y la energía de la partícula, recuperar de nuevo la relación \(E^2 = m^2 + p^2\). Podemos decir que las matrices \(\gamma\) asociadas con los operadores energía y momento están codificando, «encriptando», linealmente la famosa ecuación de Einstein.
La ecuación de Dirac es uno de los grandes logros de la Física Teórica, matemáticamente es de una simpleza sorprendente y al mismo tiempo de una riqueza física desbordante.
En lo siguiente desvelaremos algunos de sus secretos e intentaremos asociarlos a los elementos fundamentales de las interacciones.
7.2.1. Representación covariante de la ecuación de Dirac#
La representación covariante de la ecuación de Dirac es:
donde \(\partial_\mu\) es la derivada covariante que definimos como:
y \(\gamma^\mu\), con \(\mu = 0, 1, 2, 3\), son la matrices gamma.
Nota: entendemos la contracción de índices en \(\mu\) como un sumatorio:
En estos apuntes, y habitualmente en la literatura, los índices griegos, \(\mu, \nu = 0, 1,2, 3\), estarán asociados a las componente temporales y especiales, meintras que los índices latinos, \(i, j, k = 1, 2, 3\), representarán las componentes espaciales. En ambos caso si aparecen contraidos, implican un sumatorio.
Notar que \(m\) es en realidad la matrix unidad multiplicada por el valor de \(m\).
7.2.1.1. Las matrices \(\gamma\)#
Las matrices-\(\gamma\) cumplen:
con \(k=1, 2, 3\), y \(\mu = 0, 1, 2, 3\).
De forma equivalente, cumplen las siguientes relaciones de anti-conmutación:
Donde \(g_{\mu\nu}\) es la métrica de Minkowski.
Vamos a deducir estas reglas de conmutación a partir de la asociación de los operadores momento y energía con la derivas lineal en espacio y tiempo.
Si hacemos la asociación habitual de mecánica cuántica:
A partir de: $\( i\gamma^\mu \partial_\mu \, \Psi(x) = m \,\Psi(x), \\ [i \gamma^0\partial_0 + i \gamma^k \partial_k] \, \Psi(x) = m \Psi(x) \\ \gamma^0 E - \vec{\gamma} \bf{p} = m \)$
Elevándolo al cuadrado:
con \(k, i = 1, 2, 3\).
Nota: A partir de ahora no explicitaremos los sumatorios.
Si asociamos término a término, concluimos:
con \( i \neq k, \;\; i,k = 1, 2, 3\)
Esto es:
con \(\mu, \nu = 0, 1, 2, 3.\)
Veamos además que la matrix \(\gamma^0\) es hermítica y las \(\gamma^k\) anti-hermíticas:
Estas propiedades se derivan de que el hamiltoniano es hermítico, \(H^\dagger = H\), dado que sus autovalores debe ser reales.
El Hamiltoniano de Dirac es: $\( H = i \partial_0 = \gamma^0 (m -i \gamma^k \partial_k) \\ \)$
Si escribimos: $\( \gamma^0 m - i \gamma^0 \gamma^k \partial_k = (\gamma^0)^\dagger m + i (\gamma^0 \gamma^k)^\dagger \partial_k, \\ \)$
obtenemos que:
7.2.1.2. Matrix \(\gamma^5\)#
Vamos a introducir una quinta matriz, \(\gamma^5\), que va a estar muy relacionada con una propiedad que llamaremos quiralidad (ver al final del apéndice) y que juega un papel fundamental en la interacciones débiles.
La matriz \(\gamma^5\) se define:
Y tiene las siguientes propiedades:
que se derivan de las propiedades de las matrices \(\gamma^\mu\).
Cuestión: Verifica las propiedades de \(\gamma^5\)
La matrices \(\gamma^\mu\) adimiten diversas representaciones, la más común, que usaremos aquí, es la representación de Pauli-Dirac, dada por:
donde \(I\) es la matriz identidad \(2\times2\), y \(\sigma_k\) son las matrices de Pauli:
que recordemos cumplen:
Cuestión: Comprueba que las \(\gamma^\mu\) cumplen las reglas de conmutación y sus propiedades de hermicidad.
7.3. El espinor adjunto, la norma y la corriente#
En mecánica cuántica nuestra función de ondas esta normalizada, toda transformación física preserva la norma. Además exite una corriente de probabilidad que cumple la ecuación de continuidad.
Vamos a identificar ahora la norma y la corriente para los soluciones de la ec. de Dirac, pero para ello necesitamos introducir antes el espinor adjunto.
7.3.1. El espinor adjunto#
Definimos el espinor adjunto como:
En la representación de Pauli-Dirac:
que tiene forma de vector fila.
7.3.2. La ecuación de Dirac para el espinor adjunto#
La ec. de Dirac para el espinor adjunto se obtiene tras aplicar el transpuesto conjugado a la ec. de Dirac:
si primero usamos \((\gamma^0)^\dagger = \gamma^0, \, (\gamma^k)^\dagger = - \gamma^k\), luego multiplicamos por \(\gamma^0\) por la derecha, y aplicando \(\gamma^k\gamma^0 = - \gamma^0\gamma^k\), obtenemos:
Finalmente:
que es la ecuación de Dirac para el espinor adjunto.
7.3.3. Norma#
La norma asociada a las soluciones de la ecuación de dirac es:
que se trata de un escalar Lorentz, preserva unitariedad (ver extensión]y cuyo valor (por convención) se toma como \(2m\).
7.3.4. Corriente fermiónica de probabilidad#
La corriente de probabilidad fermiónica es:
donde \(\rho\), es la densidad, y \({\bf j}\) será el corriente de probabilidad del spinor de Dirac.
Notar que los cuatro elementos de la corriente corresponden al valor de los índices de \(\mu\)
En la extensión [ext-trans-Lorentz] se demuestra que efecticamente la corriente se transforma como un vector bajo transformaciones de Lorentz. Veamos aquí que cumple la ecuación de conservación:
O en forma covariante:
La densidad es:
Podemos ver primero que la corriente se conserva, esto es que cumple la ecuación de conservación:
Podemos comprobar que es cierto:
De las ecuaciones de Dirac del espinor y el espinor adjunto, tenemos que:
Si sustituimos:
Luego:
Concluimos que \(j^\mu = \bar{\Psi} \gamma^\mu \Psi\) es una corriente conservada, que llamaremos corriente fermiónica.
7.4. Soluciones de la ecuación de Dirac#
La solución de la ecuación de Dirac para un fermión libre, \(\Psi(x)\), es un cuadri-spinor de Dirac:
que tiene cuatro componentes, \(\psi_i(x)\) con \(i=1, 4\), complejas en forma vector columna.
Esto es, tiene cuatro soluciones complejas independientes.
Las cuatro soluciones se puede agrupar en dos:
las soluciones de los fermiones, \(\Psi_s(x)\),
y las de los anti-fermiones, \(\Phi_s(x)\),
cada una con dos posibilidades de espín arriba y abajo, \(s = 1, 2\) en una dirección.
Las soluciones admiten, como veremos en breve, la expresión:
Que tiene dos partes,
una parte de onda plana, \(e^{\mp i \, x \cdot p}\), que contiene toda la dependencia espacio-temporal,
y otra parte espinorial, 4 componentes puestas en forma columna, que corresponde al espinor del fermión \(u_s(p)\) y del antifermión \(v_s(p)\) con dos posibilidades de espín, \(s= 1, 2\), que dependen sólo del cuadrimomento \(p\).
Vamos a posponer la discusión de qué significan las antipartículas, y vamos a obtener primero las soluciones de la ec. de Dirac.
7.4.1. Espinores de los fermiones#
Las soluciones de los fermiones, \(\Psi_s(x) = u_s(x)\, e^{-i \, xp}\), tienen como energía:
y componentes del momento:
A aplicar la ec. de Dirac sobre la solución \(\Psi(x)\) nos queda solo la ecuación de Dirac para el espinor, \(u_s(p)\), que veremos solo depende de \(p\):
donde \(k = 1, 2, 3\), y los índices contraidos indican sumatorio.
Esto es:
Recordemos que para la subida y bajada de índices de un cuadrivector
llamamos vector contra-variante: $\( p^\mu = (E, {\bf p}) \)$
Y vector covarainte:
Podemos dar las cuatro componentes del espinor \(u_s(p)\) con dos bi-spinores, \(u^a_s(p), \, u^b_s(p)\), cada uno de ellos a su vez compuestos por dos componentes en vertical.
La ecuación de Dirac, en la representación Pauli-Dirac, sobre el espinor \(u_s(p)\) queda:
Donde estamos dando el momento \({\bf p} = \text{p} \, \hat{\bf v}\), a partir del módulo del momento \(\text{p} = |{\bf p}|\) y de su dirección \(\hat{\bf v}\).
Que nos da dos ecuaciones acopladas:
De la segunda, podemos dar el bi-espinor de abajo \(u^b_s(p)\) en función del bi-espinor de arriba, \(u^a_s(p)\):
Si definimos el factor:
Observamos que toma el valor:
\(\kappa = 0\) para el caso de la partícula en reposo, \(\text{p} = 0\),
\(\kappa = 1\) para el caso de una partícula ultra-relativista \(E \gg m\) o sin masa, \(m=0 \, (\text{p} = E)\).
La relación entre los dos bi-espinores queda simplemente:
Podemos explicitar el factor \((\hat{\bf v} \cdot \vec{\sigma})\), donde, recordemos, \(\hat{\bf v}\) es la dirección unitaria del momento, \({\bf p}\):
Dejamos como ejercicio comprobar a partir de las propiedades de las matrices \(\sigma_i\), que:
Tomemos las posibilidades del bi-espinor de arriba, \(u^a_s(p)\), con \(s=1, 2\), como:
que como veremos corresponde a un espinor con el espín alineado hacia arriba o abajo en \(z\) respectivamente.
Las dos soluciones de los espinores de los fermiones son:
Donde \(N\) es una constante de normalización, cuyo origen es cinemático (ver apéndice), y que vale:
Para el caso de un fermión en reposo, los dos posibles espinores son:
Que podemos explicitar:
7.4.1.1. proyecciones de espín#
Introducimos ahora el operador espín, \({\bf S}\):
Comprobamos que la tercera componente de espín del espinor en reposo, \(u_1(m)\) es hacia arriba, y de \(u_2(m)\) hacia abajo:
El espinor \(u_s(p)\) de un fermión que se mueve en la dirección \(z, (\hat{\bf v} = \hat{k})\), con momento \(\text{p}\) es:
Que podemos explicitar:
7.4.1.2. proyecciones de helicidad#
Definimos el operador helicidad, \(h\), como la componente (o proyección) del espín en la dirección del momento:
Para el caso de espinor \(u_s(p)\) cuyo momento va en la dirección \(z\), la tercera componente de espín y helicidad, por definición, coinciden, \(\text{S}_3 = h\).
Los espinores \(u_s(p)\) con el momento en la dirección \(z\) son autoestados de helicidad, y podemos renombrarlos:
Así:
Nota El espinor \(u_s(m)\) y \(u_s(p)\) están relacionados entre sí. El espinor \(u(p)\) corresponde al espinor en reposo, \(u_s(m)\), después de hacerle un boost en \(z\) con \(\beta \, \hat{\bf v} =\frac{\bf p}{E}\). En la sección de transformaciones veremos cómo al aplicar un boost a un espinor.
7.4.2. Espinores de los anti-fermiones#
Las soluciones de los anti-fermiones, \(\Phi_s(x) = v_s(x)\, e^{+i \, xp}\), tiene como energía:
Esto es, ¡son autoestados de energía negativa!
Y componentes del momento:
¡están invertidas!
7.4.2.1. La interpretación de las anti-partículas#
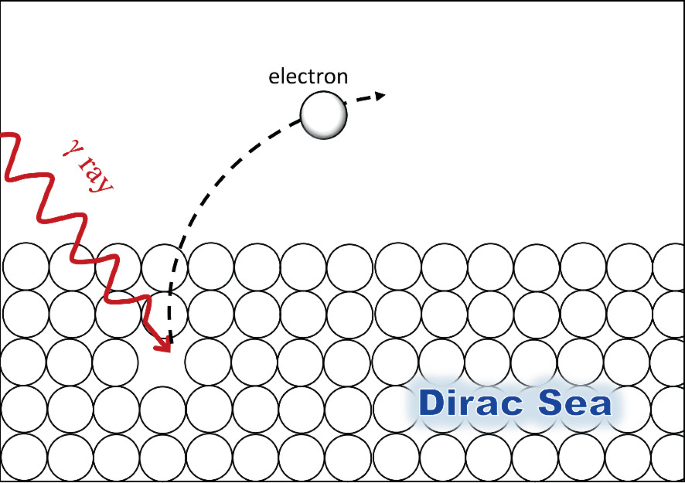
Dirac propuso una ingeniosa y iluminadora idea para explicar las soluciones de energía negativa, basada en que en el vacío todos los estados negativos están ocupados. Esta idea también se conoce como el mar de Dirac.
De tal forma que la energía mínima para crear un electrón, para hacerlo saltar de la energía negativa, es de \(2m_e\). Al hacer saltar un electrón del mar, en éste queda un hueco, que se comporta como una partícula de carga positiva: el positrón.
Imagen del mar de Dirac [Springer] |
Esta idea es muy útil en otras ramas de Física, por ejemplo aparece en los pares electrón/hueco de los semi-conductores.
Pero ¿qué sentido tiene que el mar sea infinitamente negativo, que el nivel inferior de energía no esté acotado?
7.4.2.2. Interpretación de las antipartículas#
Fue Feynman y Stückelberg quienes propusieron que las anti-partículas son «partículas que van hacia atrás en el tiempo».
inversion de phase |
Con esta interpretación, la inversion temporal implica cambiar \(t \to -t\), pero también \({\bf p} \to - {\bf p}\), con lo que la fase asociada a \(\Psi_s(x)\) cambia:
es ahora una phase como la de la partícula.
Notar que la parte espacio-temporal de la función de ondas cambia de signo, lo que recupera el signo adecuado de la energía y el momento. Veámoslo:
La anti-partícula proviene de una partícula que viaja «hacia atrás en el tiempo» y que tiene energía positiva.
En esta visión, no solo cambia de signo la energía, sino también el momento y el espín, las cantidades que se inviertan an invertir el tiempo.
La interpretación de las anti-partículas de la ecuación de Dirac es controvertida, y su sentido aparece de forma natural cuando se cuantifica el campo de Dirac, esto es, en teoría cuántica de campos.
Tanto en TCQ como experimentalmente, la antipartícula es igual que su partícula en espín, masa, vida media pero con las cargas opuestas.
7.4.2.3. Ecuación de dirac para el espinor de los anti-fermiones#
La ecuación de Dirac aplicada ahora sobre las soluciones de las antipartículas, \(\Phi_s(x)\), queda:
que traduce en una ecuación para los espinores \(v_s(p)\):
donde en \(p = (E, {\bf p})\) tanto la energía como el momento son físicas, esto es \(E >0\) y \({\bf p}\) es el momento de la antipartícula.
Si escribimos \(v_s(p)\) también con dos bi-spinores, \(v^a_s(p), \, v^b_s(p)\), cada uno a su vez con dos componentes en vertical.
la ecuación de Dirac del espinor \(v_s(p)\) en la representación Pauli-Dirac queda:
Donde estamos dando el momento \({\bf p} = \text{p} \, \hat{\bf v}\), a partir del módulo del momento \(\text{p} = |{\bf p}|\) y de su dirección \(\hat{\bf v}\).
Obtenemos de nuevo dos ecuaciones acopladas
De la primera, podemos dar el bi-espinor de arriba \(v^a_s(p)\) en función del de abajo, \(v^a_s(p)\):
Tomamos las dos posibilidades del bi-espinor de abajo, \(v^b_s(p), \;\; s = 1, 2\), como:
Los espinores de los fermiones son:
Para el caso de un anti-fermión en reposo:
De forma explícita:
En la imagen Feynman-Stückelberg en las que las antipartículas son partículas hacia atrás en el tiempo, la inversión temporal, implica también la inversión del momento angular.
Así la tercera componente del espín del espinor \(v_s(p)\) es:
Luego, \(v_1(m)\) tiene tercera componente de espín \(+1/2\) y \(v_2(m)\), \(-1/2\).
El espinor de un anti-fermión que se mueve en la dirección \(z, (\hat{\bf v} = \hat{k})\), es:
Que podemos explicitar:
En la interpretación Feynman-Stückelberg, la inversión temporal no afecta al operador helicidad, porque se produce un cambio de signo en el momento angular y el momento que se cancelan:
Luego en este caso \(v_+(p) = v_1(p)\) y \(v_-(p) = v_2(p)\)
Así pues, las cuatro soluciones generales de la ecuación de Dirac son:
donde \(s = 1, 2\).
7.4.3. Soluciones autoestados de helicidad#
El operador helicidad corresponde por definición a la componente del espín en la dirección del movimiento, \(\hat{\bf v}\). De ahí que en el caso de una partícula moviéndose en \(z\), la componente \(z\) del espín y la helicidad coincidan.
Nos podemos preguntar ahora cuáles son las soluciones de la ec. de Dirac que son a su vez autoestados de helicidad, esto es que tienen su espín alineado con el momento.
Los autovalores de helicidad, como los de tercera componete de spín, son \(\pm 1/2\).
Lo que se traduce:
Que se traduce en dos ecuaciones, pero la segunda es una identidad si se cumple la primera:
Vamos a encontrar pues el bi-espinor, \(\chi_r(\hat{\bf v})\), que cumple
que vemos que depende ahora de \(\hat{\bf v}\).
Si escribimos explícitamente:
La condición de las dos componentes \(a, b\) de \(\chi_r(\hat{\bf v})\) es:
Esto es, con \(\lambda = \pm 1\):
Por lo tanto, las componentes \(a, b\) cumplen:
Para el caso de helicidad positiva \(\lambda = +1\), obtenemos:
Resolviendo también para \(\lambda = -1\), imponiendo que tienen norma unidad, y haciendo uso que sin pérdida de generalidad podemos tomar la componente de arriba, \(a\), como real, los bi-espinores quedan:
Notar que el bi-espinor definido antes, \(\chi_s\), es simplemente \(\chi_r(\hat{k})\), que corresponde a seleccionar como dirección \(\hat{\bf v} = \hat{k}\).
De forma similar, los bi-espinores de los anti-fermiones que son autoestados de helicidad quedan:
Así pues, los espinores autoestados de helicidad que son soluciones de la ec. de Dirac son entonces:
donde \(r = \pm, \, \lambda_\pm = \pm\).
Si reescribimos explícitamente los espinores de helicidad en la dirección \(z\), (\(\theta = \phi = 0\)), volvemos a obtener:
con el factor de normalización \(N = \sqrt{E+m}\)
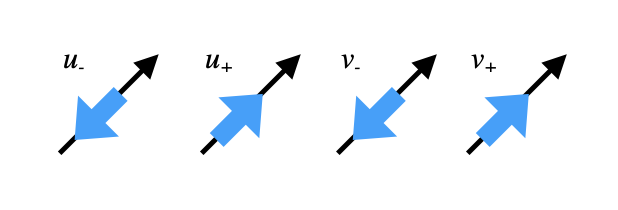
Los espinores de quiralidad se suelen representar de forma gráfica con la siguientes figuras:
spín (flecha azul) y momento (negra) de los spinores de helicidad |
\(u_\pm(p), v_\pm(p)\) son los espinores de las partículas y antipartículas respectivamente.
\(u_{+}(p), v_{+}(p)\) son espinores de helicidad positiva (el espín tiene el mismo sentido que el momento).
\(u_{-}(p), v_{-}(p)\) tienen helicidad negativa (el spín y momento tienen sentido opuesto).
Nota: Podemos reinterpretar el espinor \(u_+(p)\) como aquel que se obtiene de rotar un espinor inicialmente en \(u_1(p)\), con su espín alineado en la dirección hacia arriba en \(z\), hasta situar su espín alineado con \(\hat{\bf v}\), con la dirección y sentido del momento, \({\bf p}\).
En la sección sobre transformaciones Lorentz, trataremos de nuevo la rotación del espinor.
7.5. Quiralidad#
La violación de paridad de las interacciones débiles está relacionada con una propiedad del espinor de Dirac, llamada quiralidad.
Decimos que un espinor tiene quiralidad a derechas o izquierdas si es autoestado de \(\gamma^5\) con autovalores +1 y -1 respectivamente. Esto es:
La quiralidad es una propiedad matemática que no tiene un equivalente simple físico. Contrariamente a la helicidad, que si tiene un equivalente físico: la proyección del espín en la dirección el momento.
Veremos que un espinor de Dirac puede descomponerse en un espinor de quiralidad a izquierdas y otro a derechas, tales que la inversión de paridad intercambia la quiralidad, la derecha por la izquierda y viceversa.
Esto hace que una interacción que sea invariante por paridad, no hará distinción entre los dos quiralidades, pero una que sí lo haga, favorecerá o incluso suprimirá una quiralidad.
Los proyectores de quiralidad son:
De tal forma que \(\Psi(x)\) se descompone en dos partes, a izquierdas y derechas.
Los proyectores son en realidad dos matrices que están actuado sobre la parte espinorial de \(\Psi(x)\).
Vemos que efectivamene un espinor de quiralidad a derechas o izquierdas cumple:
Esto es para los espinores de los fermiones, actuan sobre \(u(p)\):
donde hemos eliminado el subíndice \(s\) de los espinores \(u_s(p)\) por simplicidad.
Vamos a comprobar que se trata de proyectores.
Estos deben cumplir:
La primera es inmediata.
Comprobemos que \(P^2_R = P_R\)
dado que \((\gamma^5)^2 = I\).
De igual manera obraríamos con \(P^2_L = P_L\)
Y finalmente, \(P_L \, P_R = P_R \, P_L = 0\):
Vamos a aplicar paridad sobre \(u_L(p), \; u_R(p)\), recordemos que la representación espinorial de la inversión por paridad es \(S(P) = \gamma^0\)
Luego la inversión por paridad nos intercambia los espinores de quiralidad a derechas por izquierdas y viceversa:
Para los espinores de los antifermiones definimos la quiralidad de forma complementaria a la de los fermiones, esto es:
Igualmente la inversión por paridad intercambia sus quiralidades
7.5.1. Las espinores en su expresión quiral#
Si los aplicamos sobre los espinores de Dirac que son autoestados de helicidad. Recordémos que son:
donde \(r = \pm, \, \lambda_\pm = \pm 1\).
Obtenemos:
Que podemos explicitar en la siguiente tabla:
helicidad \(\downarrow\) \ quiralidad \(\rightarrow\) |
— R — |
— L — |
|---|---|---|
+ |
\(\frac{1}{2}(1+\kappa)\) |
\(\frac{1}{2}(1-\kappa)\) |
- |
\(\frac{1}{2}(1-\kappa)\) |
\(\frac{1}{2}(1+\kappa)\) |
En el caso en el que la partícula es ultra-relativista \(E \gg m\) o sin masa, \(m=0\), esto es, cuando \(\kappa = 1\)
En ese caso el espinor de helicidad negativa solo tiene componene de quiralidad a izquierdas. Y el espinor de helicidad positiva solo quiralidad a derechas.
solo cuando \(\kappa = 1\).
Que si explicitamos para el caso \(\hat{\bf v} = \hat{k}\), esto es, elegimos el eje \(z\) como la dirección de movimiento de la partícula.
y en el caso ultra-relativista,
Donde, recordemos \(N = \sqrt{E + m } = \sqrt{E}\)
Para los espinores de los antifermiones:
que si explicitamos para el caso \(\hat{\bf v} = \hat{k}\) y en el caso ultra-relativista,
Podemos especificar los proyectores de quiralidad en la representación Pauli-Dirac:
7.5.2. La representación Weyl o quiral#
Vamos a considerar la representación de Weyl (o quiral) de las matrices \(\gamma^\mu\):
Con lo que que:
Esto es el espinor de Dirac está compuesto de dos bi-espinores, \(u_L, u_R\), llamados de Weyl, que corresponden con la parte de quiralidad a izquierdas y a derechas del espinor de Dirac.
Si ahora consideramos el caso revelador de un fermión sin masa \(m=0\), la ec. de Dirac queda:
que se descompone en dos ecuaciones independientes:
Esto es, el espinor de Dirac se compone de dos espinores de Weyl independientes.
O en otras palabras, es el término de masa en la ec. de Dirac, la que hace que los dos espinores de Weyl estén conectados.
dado que \(E = \text{p}\), donde \({\bf p} = \text{p} \hat{\bf v}\), estas ecuaciones son equivalentes a:
Esto es, hay una conexión uno a uno entre helicidad y quiralidad. El espinor de Weyl a izquierdas tiene helicidad negativa y el de derechas positiva.
En este caso de las partículas sin masa, quiralidad y la helicidad son ambas propiedades estacionarias e invariantes Lorentz.
En el Modelo Estándard este caso correspondía al neutrino.
7.5.3. la norma y la corriente bajo quiralidad#
Como \((\gamma^5)^\dagger = \gamma^5\), los projectores no se ven afectados por la operación \(\dagger\):
Mientras que el intercambio con \(\gamma^0\) intercambia los proyectores:
Esto separa en dos las formas invariantes Lorentz
Para la escalar \(\bar{\Psi}(x) \Psi(x)\), si la escribimos solo en función de sus espinores \(\bar{u}(p) u(p)\):
Y de forma recíproca:
Luego la forma escalar:
Se compone de dos partes donde las dos quiralidades se acoplan una a la otra.
Esto implica que un término escalar en el Lagrangiano (el que estará asociado a la masa) exige la existencia de las dos quiralidades.
Recordando que \(\gamma^5\gamma^\mu = - \gamma^\mu\gamma^5\), vemos que:
el intercambio de lado de \(\gamma^\mu\), intercambia los proyectores.
Veamos ahora cómo queda la forma vectorial, \(\bar{\Psi}(x)\gamma^\mu\Psi(x)\) escrita en sus componentes de quiralidad. Desarrollamos nuevamente la expresión con os espinores, \(\bar{u}(p) \gamma^\mu u(p)\).
De forma similar:
Así la forma vectorial queda:
Esto es la corriente se divide en dos, una corriente de quiralidad a izquierdas y otra a derechas.
En resumen: