Boletín de problemas - preliminar
11. Boletín de problemas - preliminar#
Jose A. Hernando
Departamento de Física de Partículas. Universidade de Santiago de Compostela
Octubre 2024
import time
print(' Last version ', time.asctime() )
Last version Wed Dec 18 17:08:26 2024
# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2
# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.constants as units
print('hbar = {:4e} J/s'.format(units.hbar))
print('c = {:4e} m/s'.format(units.c))
GeV_to_Julio = units.giga * units.eV
print('GeV = {:4e} J '.format(GeV_to_Julio))
hbarc = units.hbar * units.c / (GeV_to_Julio * units.femto) # GeV fm
print('hbar c = {:4e} GeV fm'.format(hbarc))
hbar = 1.054572e-34 J/s
c = 2.997925e+08 m/s
GeV = 1.602177e-10 J
hbar c = 1.973270e-01 GeV fm
problema 1
Considera que el protón pudiera desintegrarse a \(p \to e^+ + \pi^0\) y considera el límite en el tiempo parcial de vida media publicado en SK¿Cómo compara con la edad del Universo? ¿Qué cantidad de agua necesitarías para detectar u obtener un límite de la vida media del protón mejor que el actual considerando que se desintegran los protones del H del agua? Los artículos en HEP aparecen habitualmente en el siguiente archivo y en la base de datos INSPIRE. ¿Puedes encontrar cuál es el artículo más citado del experimento SuperKamiokande?
solución
Del artículo obtenemos
La edad del universo es aproximadamente \(13.7 \times 10^{9}\) años.
Cuestión ¿Es la desintegración, \(p \to e^+ + \pi^0\), posible?
No, no lo es porque violaría el número leptónico y el número bariónico.
Comentario: Sin embargo no viola B-L. B-L se debe conservar para que no se cree carga eléctrica neta.
Cuestión ¿Qué significa \(\tau/B\)?
Es el tiempo de vida parcial de esa desintegración, la posible \( p \to e^+ + \pi^0\), pero el protón pudiera desintegrarse de otras formas, a otros canales.
Recordemos la relación entre anchura de desintegración y tiempo de vida:
La anchura total se obtiene de la suma de las parciales:
Y la fracción de desintegración \(\mathcal{B}_i\)
Esto es la vida parcial
Cuestión ¿Cuál es la masa necesario para poner un límite mejor que el actual en este canal?
En realidad se trata de le exposición: kton año
Sea \(M\) la masa de agua en g, sea \(M_A = 18\) g/mol, siendo \(N_A\) el número de Avogadro, el número de protones \(N\) del Hidrógeno es:
Si tenenos \(N\) protones y la vida media es \(\tau\) en \(t=1\) año sobreviven, dado que \(t \ll \tau\):
donde \(\tau\) aquí es la vida media parcial \(\tau_i\), pero omitimos el sub-índice.
En un año \(t=1\) se han desintegrado
¿Qué masa necesitamos para ver una desintegración si la cuota \(\tau\) fuera el valor real?
tau = 2.4e34 # partial proton mean lifetime
NA = units.N_A # Avogadro number
MA = 18 # g/mol
M = tau * MA/(2*NA)
print('water mass {:1.2e} k tons'.format(M*(1e-9)))
water mass 3.59e+02 k tons
Cuestión Si \(\tau\) es tal que para \(N_0\) esperamos en un año \(t=1\), \(\nu = 1\) eventos, ¿qué podemos esperar? ¿Siempre mediremos 1 evento? ¿qué distribución sigue?
No, no siempre medimos 1 evento, la distribución de las medidas sigue una distribución de poisson, Porque la probabilidad de que se produzca una desintegración es \(1/\tau\), ridículamente pequeña, y el número de intentos de intentos muy alto, luego la binomial original con \(p\) muy pequeña y \(N\) intentos altos, es una distribución de poisson con \(\nu = p N = 1\), siendo \(p = 1/\tau\)
from scipy.stats import poisson
nu = 2
ns = np.arange(12)
plt.bar(ns, poisson.pmf(ns, nu))
plt.xlabel(r'$n$'); plt.ylabel(r'pmf$(n | \nu)$'); plt.grid();
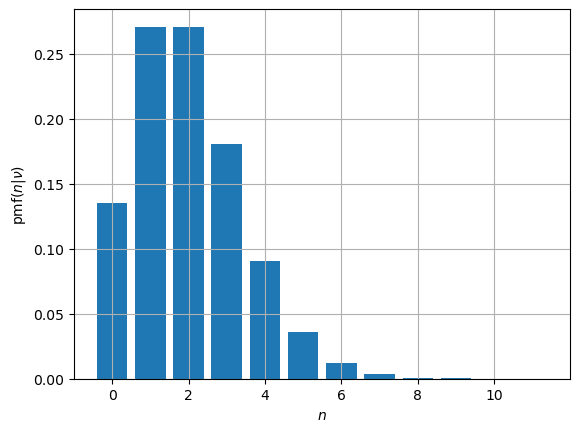
Cuestión ¿Qué límite ponemos a la vida media al 90% CL si al hacer un experimento observamos 0 eventos?
Decimos, por convención, que los valores excluidos del parámetro relevante (en este caso la vida media) al 90% CL son aquellos valores que nos daría una probabilidad de obtener un resultado como el que hemos obtenido o peor menor del 10%.
La cuestión se convierte entonces en ¿Cuál es la probabilidad de medir 0 si la media de Poisson es \(\nu\)? ¿Cuándo dicha probabilidad es menor del 10% (esto es el límite al 90%CL)?
nus = np.arange(0.1, 4, 0.1)
plt.plot(nus, poisson.pmf(0, nus)); plt.grid(); plt.plot((0, 4), (0.1, 0.1))
plt.xlabel(r'$\nu$'); plt.ylabel(r'pmf$(0 | \nu)$');
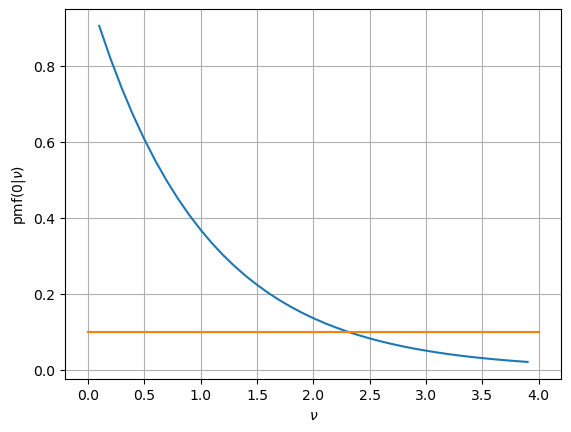
Esto es si no observamos ninguna desintegración. \(n = 0\), en un año \(t=1\), en \(N_0\) protones el valor del posible \(\nu\) que nos daría que nuestro resultado de obtener 0 tiene una probabilidad menor del 10% (de ahí el 90% CL), es 2.4.
Luego, si medimos \(n=0\), al 90% CL le corresponde un valor \(\nu = 2.4\), luego el valor del límite \(\tau\) se obtendría de:
Nota Esto no quiere decir que el valor \(\tau\) del límite no sea el valor verdadero, existe todavía un 10% de posibilidades de con ese valor, si realizase un experimento obtuvera un resultado como el que obtenido (en este caso 0) o peor.
Cuestión ¿Qué pasa en el caso más general? ¿Qué región de nuestro parámetro \(\tau\) decimos que esta excluida al 90% CL?
En el caso general al hacer un experimento de búsqueda de una nueva señal esperamos encontrar en nuestra muestra \(b\) eventos de fondo (distribuidos poisson, siendo \(b\) pequeño) y observamos \(n\), por lo que necesitamos una construcción que nos permita encontrar a partir de \((b, n)\) qué valores teóricos \(\nu\) de señal nos darían una probabilidad de obtener una observación como la que hemos obtenido o peor menor con un 10% probabilidades.
La construcción moderna se debe a dos físicos de neutrinos, G. Feldman y B. Cousins, que proposieron un método que lleva su nombre.
Cuestión ¿Cuál es el artículo más citado?
En INSPIRE seleccionar experimento SuperKamiokande, luego en ordenar artículos escoger “most cited”,
«Evidence for oscillation of atmospheric neutrinos», hep-exp/9807003, Phys. Rev. Lett 81, 1562-1567,1998
Cuestión Lee el abstract. Nota la precaución con la que indican la posible presencia de oscilaciones, por las que después el director del experimento. T. Kajita recibiría el premio Nobel en 2015.
2) Problema
¿Cuál es la masa del neutrino? ¿Qué experimento tiene la cuota más baja hasta la fecha? Los experimentos de oscilaciones de neutrinos han medido no obstante las dos diferencias de masas al cuadrado entre los tres neutrinos existentes. \(\Delta m^2_{21} = m^2_2 - m^2_1\), es la diferencia de masas al cuadrado entre el neutrino 2 y el 1. Si los resultados experimentales son \(\Delta m^2_{21} = 7.5 \times 10^{-5}\) eV\(^2\), y \(|\Delta m^2_{31}| = 2.5 \times 10^{-3}\) eV\(^2\). ¿Puedes hacer un gráfico de la masa de los neutrinos en función de la masa del más ligero?
Solución
La melor cuota de la masa del neutrino la ha publicado el experimento KATRIN en 2024, arXic.2406.13517 y es \(m_\nu \lt 0.45\) eV al 90% C.L.
Sabemos que la masa del neutrino \(m_2 \gt m_{light}\), siendo \(m_{light}\) el más ligero, pero nos sabemos, dado que solo conocemos el valor absoluto de \(|\Delta m^2_{31}|\), si el neutrino 1 o el neutrino 3 son los más ligeros.
Vamos
dm21 = 7.5e-5
dm31 = 2.5e-3
m0 = np.array((1e-5, 1e-4, 1e-3, 5e-3, 1e-2, 5e-2, 1e-1, 5e-1, 1.))
m2 = lambda m0 : np.sqrt(dm21+m0**2)
mup = lambda m0 : np.sqrt(dm31+m0**2)
plt.subplot(1, 2, 1)
plt.plot(m0, m0, label = r'$m_1$'); plt.plot(m0, m2(m0), label = '$m_2$'), plt.plot(m0, mup(m0), label = 'm3')
plt.xscale('log'); plt.yscale('log'); plt.legend(); plt.xlabel(r'$m_{light}$ (eV)'); plt.ylabel(r"(eV)"); plt.grid(); plt.title('Normal')
plt.subplot(1, 2, 2)
plt.plot(m0, m0, label = r'$m_3$'); plt.plot(m0, mup(m0), label = '$m_1$'), plt.plot(m0, mup(m0) + m2(m0), label = 'm2')
plt.xscale('log'); plt.yscale('log'); plt.legend(); plt.xlabel(r'$m_{light}$ (eV)'); plt.ylabel(r"(eV)"); plt.grid(); plt.title('Inverted')
Text(0.5, 1.0, 'Inverted')
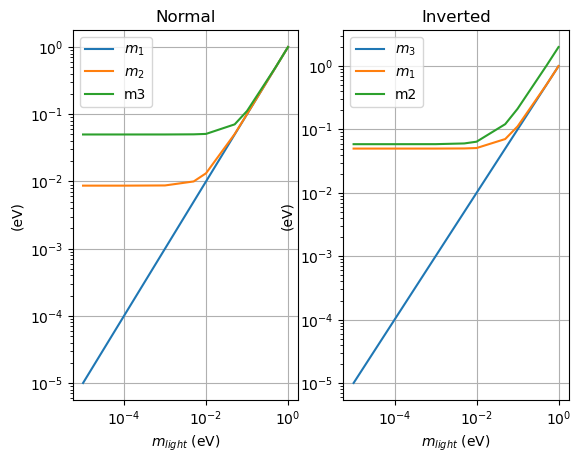
**problema A partir de los datos del PDF elabora una tabla con la masa, carga, espín, paridad, vida media y desintegración principal de los leptones.
\(e\) |
\(\mu\) |
\(\tau\) |
\(\nu\) |
|
|---|---|---|---|---|
masa |
0.511 MeV |
105.7 MeV |
1777 MeV |
\(\le\) 1 eV |
carga |
-1 |
-1 |
-1 |
0 |
vida media (\(\tau\)) |
estable |
\(2.197\) \(\mu\mathrm{s}\) |
\(290.6\) fs |
estable |
Fracción de desintegración |
|
|---|---|
\(\mu \to e + \bar{\nu_e} + \nu_\mu\) |
\(\sim 100\) % |
\(\tau \to \mu + \bar{\nu_\mu} + \nu_\tau\) |
\(17.4\) % |
\(\tau \to e + \bar{\nu_e} + \nu_\tau\) |
\(17.8\) % |
\(\tau \to \mathrm{hadrons}+ \nu_\tau\) |
\(\sim 64\) % |
Crea una segunda tabla con la composición de quarks, masa, carga, espín, paridad, vida media y desintegración principal de los siguientes mesones $\pi^\pm, \pi^0\(, \)K^\pm,\( \)K^0, D^\pm, D^0, J/\Psi, \Upsilon, B^0, B^0_s$.
nombre |
quark composition |
\(J^{P}\) |
mass (MeV) |
life-time |
main decays |
|---|---|---|---|---|---|
\(\pi^0\) |
\((\bar{u}u, \bar{d}d)\) |
\(0^-\) |
\(134.97\) |
\(8.43\pm0.6 \, 10^{-17}\) s |
\(2\gamma\) (98%) |
\(\pi^\pm\) |
(\(u\bar{d}, \bar{u}d\)) |
\(0^{-}\) |
\(139.57\) |
\(26.033\pm0.05\) ns |
\(\mu + \bar{\nu}_\mu\) (98%) |
\(\rho\) |
(\(u\bar{u}, \bar{d}d\)) |
\(1^-\) |
\(7775.5\pm0.4\) |
\(194.4\pm1\) MeV |
\(2\pi\) |
\(K^\pm\) |
\((\bar{s}u, s\bar{u})\) |
\(0^{-}\) |
\(493.677\pm 0.016\) |
\(12.39\pm0.02\) ns |
\(\mu+ \bar{\nu}_\mu\) (63%), \(\pi^- \pi^0\) (20 %) |
\(K^0_S\) |
\((\bar{s}d, \bar{d}s)\) |
\(0^{-}\) |
\(497.648\pm0.022\) |
\(89.5\pm0.05\) ps |
\(\pi^++\pi^-\) (69%), \(2\pi^0 \) (30%) |
\(K^0_L\) |
\((\bar{s}d, \bar{d}s)\) |
\(0^{-}\) |
\(497.648\pm0.022\) |
\(51.14\pm0.21\) ns |
\(\pi^\pm + e^\pm + \nu_e\) (40%), \(\pi^\pm + \mu^\pm + \bar{\nu}_\mu\) (27%) |
\(\phi\) |
\((s\bar{s})\) |
\(1^-\) |
\(1019.46\pm0.019\) |
\(4.26\pm0.05\) MeV |
\(K+\bar{K}, \pi^++\pi^-+\pi^0\) |
\(D^\pm\) |
\((c\bar{d},d\bar{c})\) |
\(0^{-}\) |
\(1869.3\pm0.4\) |
\(0.500\pm 0.007\) ps |
\(K+...\) |
\(D^0, \bar{D}^0\) |
\((c\bar{u},u\bar{c})\) |
\(0^{-}\) |
\(1864.5\pm0.4\) |
\(0.410\pm 0.002\) ps |
\(K+...\) |
\(B^0, \bar{B}^0\) |
\((b\bar{d},d\bar{b})\) |
\(0^{-}\) |
\(5279.4\pm0.5\) |
\(1.530\pm 0.009\) ps |
\(D+...\) |
\(B^0_s, \bar{B}^0_s\) |
\((b\bar{s},s\bar{b})\) |
\(0^{-}\) |
\(5367.5\pm1.8\) |
\(1.466\pm 0.059\) ps |
\(D^\pm_s+...\) |
\(J/\Psi\) |
\((c\bar{c})\) |
\(1^{-}\) |
\(3096.92\pm0.011\) |
\(93.4\pm2.1\) keV |
hadrons (87%), \(\mu+\mu^+, e+e^+\) (6%) |
\(\Upsilon\) |
\((b\bar{b})\) |
\(1^{-}\) |
\(9460.3\pm0.3\) |
\(31.98\pm2.63\) keV |
\(l+l^+\) |
problema Identifica los bariones que se forman con los quarks ligeros \((u, d, s)\).
nombre |
quark composition |
\(J^{P}\) |
mass (MeV) |
life-time |
main decays |
|---|---|---|---|---|---|
\(p\) |
(uud) |
\(1/2^+\) |
\(938.27\) |
\(>3.6 \, 10^{29}\) y |
None |
\(n\) |
(udd) |
\(1/2^+\) |
\(939.56\) |
\(874.4\pm0.6\) s |
\(p +e +\bar{\nu}_e\) (100%) |
\(\Delta\) |
(uuu) |
\(3/2^+\) |
\(1232 \pm 2\) |
\(118 \pm 2\) MeV |
\(p + \pi^-, n+ \pi^0\) |
\(\Lambda\) |
(uus) |
\(1/2^+\) |
\(1115.683 \pm 0.006\) |
\(263 \pm2\) ps |
\(p + \pi^0, n+ \pi^+\) |
\(\Sigma^0\) |
(uds) |
\(1/2^+\) |
\(1182.64 \pm 0.02\) |
\(7.4 \pm 0.7 \, 10^{-20}\) s |
\(\Lambda+\gamma\) |
\(\Omega^-\) |
(sss) |
\(3/2^+\) |
\(1672.45 \pm 0.29\) |
\(82.1\pm 1.1\) ps |
\(\Lambda+K^+, ...\) |
Sobre el descubrimiento de \(\Omega^-\)
problema Sean \(\Lambda \rightarrow p + \pi^-\) y \(\Xi^- \rightarrow \Lambda+\pi^-\). ¿Cuál es la carga de \(\Lambda\)? Indica si \(\Lambda\) y \(\Xi^-\) son bariones o mesones. Indicas sus masa, sus vidas medias y su fracción de desintegración. ¿Qué tipo de desintegración es, débil o fuerte?
Del PDG
\(m(\Lambda) = 1115.683 \pm 0.006\) MeV, \(\mathcal{Br}(\Lambda \to p + \pi^-) = 63.9 \pm 0.5\) %, \(\tau = (2.632 \pm 0.02) \, 10^{-10}\) s
Del PDG
\(m(\Xi^-) = 1321.71 \pm 0.07\) MeV, \(\mathcal{Br}(\Xi^- \to \Lambda + \pi^-) = 99.9\) %, \(\tau = (1.639 \pm 0.015) \, 10^{-10}\) s
Los dos son bariones, \(\Lambda\) tiene carga 0, y por el valor de la vida media se desintegran débilmente.
problema Recientemente el CERN ha festejado su 70 aniversario. ¿Indica cuáles han sido los dos grandes colionadores del CERN y sus parámetros principales? ¿Cuáles son los hitos y descubrimientos principales realizados en el CERN?
Aceleradores
LHC protón-protón colisions at 7, 13 TeV CM energy
LEP, e+ + e- colider at 91 GeV CM Energy and up to 200 GeV in Run-II
problema Investiga brevemente la bibliografía y contribuciones de los siguientes físicos: Paul Dirac, Ettore Majorana, Wolfgang Pauli, Enrico Fermi, Richard Feynman, Chien-Shiung Wu, Bruno Pontecorvo, Sheldon Glashow, Steven Weinberg, Abdus Salam y Peter Higgs.
problema Identifica el objetivo, detectores, periodo de operación y tamaño de los siguientes experimentos: SuperKamiokande, ATLAS, LHCb, IceCube, ALEPH, DELPHI, Gargamelle, BaBar, UA1, Gerda y SNO.