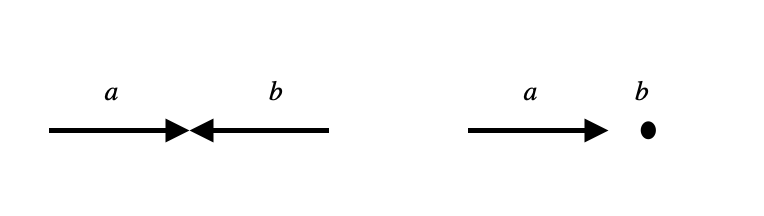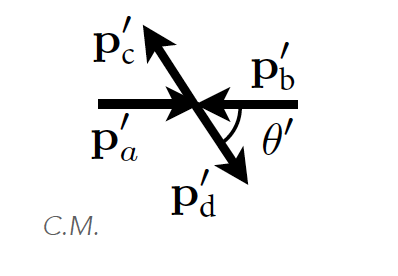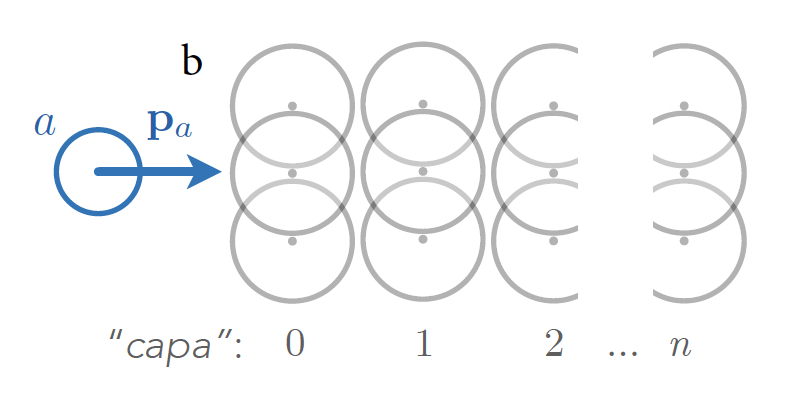Introducción a Física de Partículas
Contents
1. Introducción a Física de Partículas#
import time
print(' Last version ', time.asctime() )
Last version Mon Sep 29 15:09:14 2025
# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2
# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.constants as units
1.1. Objetivos#
Una visión del campo de la Física de Partículas:
su propósito, sus relaciones con otras ramas de la Física y los laboratorios principales.
Conceptos básicos: Interacciones y cantidades conservadas
Sección Eficaz y vida meda
radiaciones alpha, bega, gamma. De los nucleos a los quarks.
Una introducción general del Modelo Estándar:
de los componentes de la materia (fermiones) y de las fuerzas (bosones) que median entre ellas.
1.2. Sobre la Física de Partículas#
La Física de Partículas es la rama de la Física que estudia los corpúsculos más pequeños (algunos de ellos quizás elementales) de la Naturaleza y las interacciones que median entre ellos.
1.2.1. Escala de la Física de Partículas#
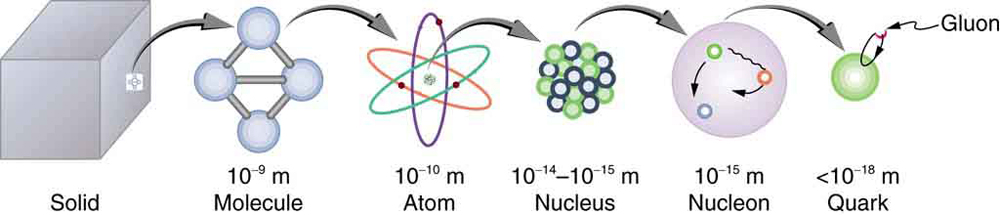
La siguiente figura muestra las diferentes escalas en distancia (m). Conforme reducimos la escala pasamos del sólido, al átomo, al núcleo, y finalmente a las partículas.
La escala en distancia que corresponde a la Física de Partículas es inferior al femtometro, \(< 10^{-15}\) m.
Profundizamos en el interior de las partículas usando otras partículas como sonda, por ejemplo electrones.
Para explorar distancias cada vez más pequeñas, por la relación de Broglie, \(\lambda = h /p\), necesitamos cada vez sondas con energías mayores.
La siguiente tabla muestra las escalas típicas de distancia (m) y energía (eV):
Atómica |
Nuclear |
Partículas |
|
|---|---|---|---|
distancia (m) |
\(10^{-10}\) |
\(10^{-14}\) |
\(10^{-18}\) |
Energía (eV) |
\(1\) |
\(10^{6}\) |
\(10^{9-11}\) |
\(\mathcal{O}\)(eV) |
\(\mathcal{O}\) (MeV) |
\(\mathcal{O}\)(GeV-TeV) |
En rango de energías de Física de Partículas es \(>\) GeV.
Por eso a la Física de Partículas también se la conoce como Física de Altas Energías.
En general, a estas energías, las partículas son relativistas. Así que nuestro entorno será la física cuántica y relativista.
1.2.2. Metodología#
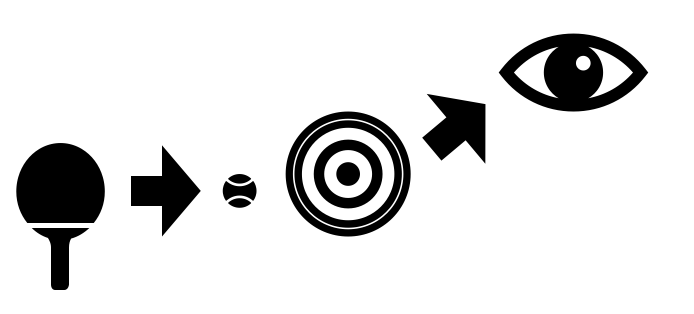
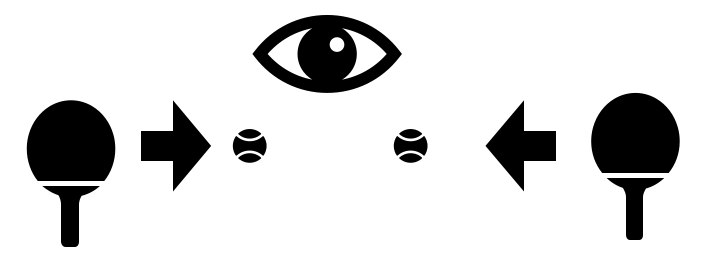
Estudiamos las interacciones de las partículas mediante dos tipos de experimentos: dispersión (scattering) o colisiones.
Esquema de dispersión |
Esquema de colisión |
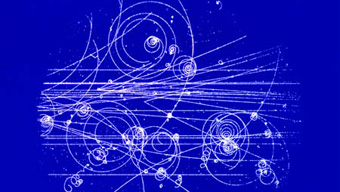
Literalmente lanzamos haces de partículas (principalmente \(e, p, \nu\)) a muy altas energías (GeV-TeV) contra blancos (formados por otras partículas, principalmente nucleones) y observamos las partículas que se producen y sus distribuciones en energía y angulares.
1.2.3. Física de Altas energías y aceleradores#
En general la materia ordinaria, a excepción de los rayos cósmicos, no es relativista.
¿Cómo podemos obtener haces de partículas a altas energías?
Mediante aceleradores de partículas como el LHC [>], o mediante los rayos cósmicos que alcanzan la Tierra (principalmente protones, pero también neutrinos) producidos en estructuras del Cosmos que actuan como aceleradores naturales.
Por ejemplo el detector IceCube [>] detecta interacciones de neutrinos atmosféricos, solares y cósmicos.
1.2.4. Partículas y Cosmología#
La Física de Partículas está muy relacionada con la Cosmología.
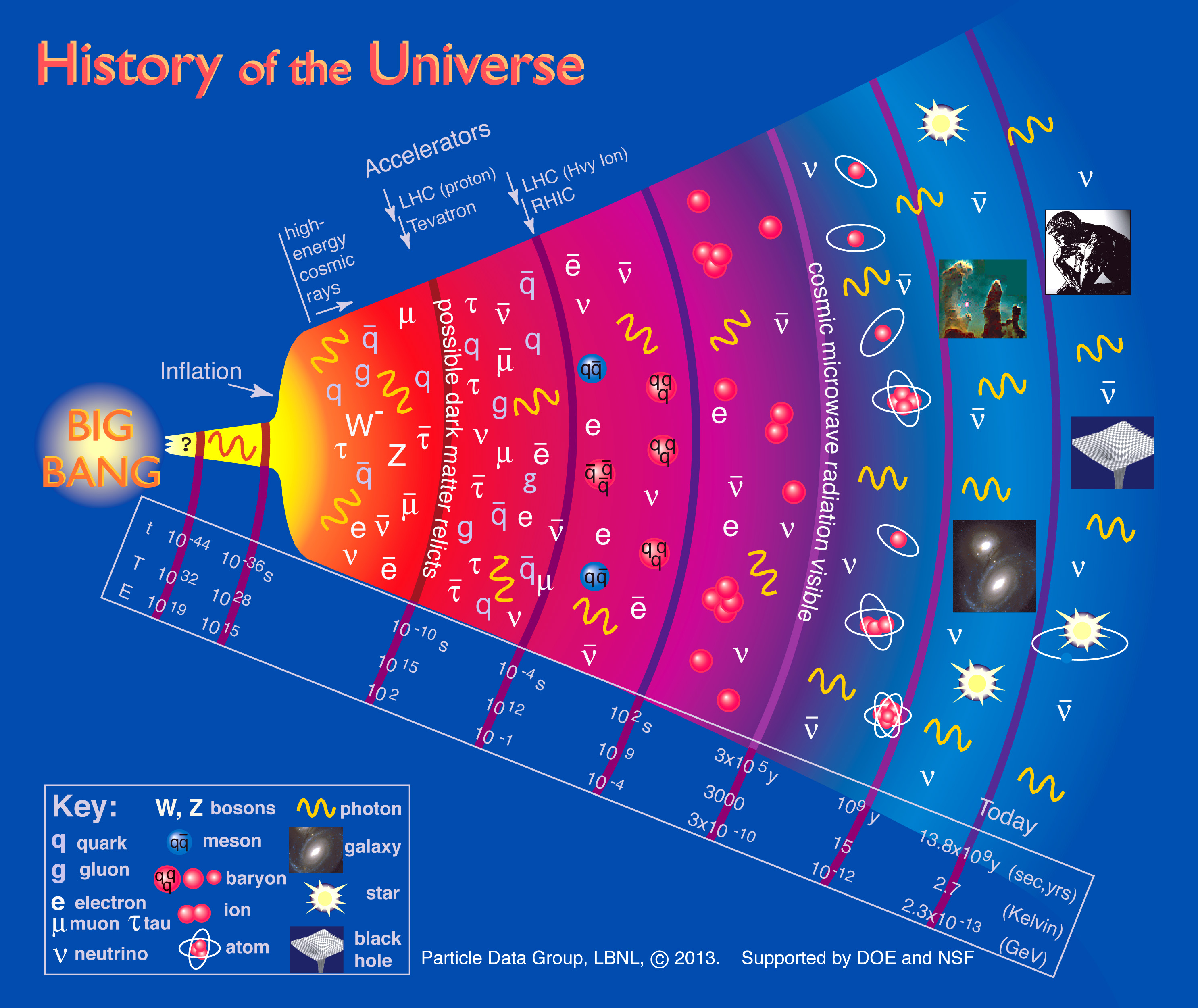
Durante los primeros segundos del Universo, éste se componía de una sopa de partículas.
Esquema de la evolución del Universo [PDG] |
Conforme el Universo se enfrió, las partículas crearon primero bariones, luego núcleos, átomos, y finalmente las estrellas y galaxias.
A partir de \(10^{-32}\) s después del Big Bang, el Universo se rige por el Modelo Estándar hasta 100 s después cuando empiezan a formarse núcleos.
Detengámanos por ejemplo, en la desintegración del neutrón, la desintegración \(\beta\)
Después de su creacción, el neutrón vive aproximadamente 10 mins, tiempo suficiente afortunadamente para que se formasen los primeros núcleos de Helio estables, lo que sucedió aproximadamente a los 6 mins.
Podemos decir por lo tanto que existe una relación de continuidad entre ramas de la física:
El Instituto Galego de Física de Altas Enerxías, IGFAE, cubre las tres ramas y sus posibles aplicaciones. Puedes explorar su página web para más información.
1.2.5. Relación entre teoría, experimentos y detectores#
La Física de Partículas involucra a la física teórica, experimental y la de detectores.
Las tres son esenciales y se complementan:
Los avances en detección hacen posible nuevos descubrimientos
Los descubrimientos marcan las líneas permitidas de las teorías
La teoría indica qué experimentos son de interés
Pero no unicamente, La física de Partículas necesita de la ingeniería, química y computación.
1.2.6. La gran ciencia#
Los aceleradores y los experimentos de partículas son grandes construcciones, en muchas ocasiones únicas y singulares, que requieren de la participación de cientos o miles de científicos y una gran financiación.
Los experimentos son muy complejos. Su planificación, construcción y explotación duran a veces décadas. Por ejemplo, ATLAS en el LHC,
Imagen del detector ATLAS durante su construcción [ATLAS] |
es uno de los más grandes experimentos construidos y donde trabajan más de 2000 físicos del todo el mundo.
1.2.7. Los grandes Laboratorios#
Los experimentos de Física de Partículas tienen lugar principalmente en grandes laboratorios internacionales.
El CERN, en Ginebra, Suiza, fundando en los años 50 del siglo XX, es desde los 80 el principal laboratorio de Física de Partículas. El CERN es un gran campus europeo de investigación donde han tenido lugar experimentos esenciales en Física de Partículas, avances fundamentales como la aparición de la WWW, y descubrimientos como los de los bosones vectoriales \(W^\pm, Z^0\) y el Higgs.
La actual directora del CERN es F. Gianotti.
F. Gianotti, directora del CERN |
Los principales laboratorios de partículas son:
basados en aceleradores:
CERN (Ginebra, Suiza).
Fermilab (Chicago, Illinois), SLAC (Stanford, California), Brookhaven (New York)
KEK (Japón)
y subterráneos:
1.2.8. Aplicaciones prácticas#
Las técnicas de construcción de los detectores y de desarrollo de los algoritmos de tratamiento de datos han dado lugar a aplicaciones importantísimas en otros campos:
en Física Médica, como por ejemplo, los rayos-X, o la terapia hadrónica.
o la aparición de la World Wide Web (WWW), quizás unos de los momentos revolucionaros de la Humanidad.
La web se desarrolló en el CERN para poder presentar y compartir la información.
1.3. Conceptos básicos#
1.3.1. Interacciones#
Las interacciones, tanto las nucleares como las de las partículas, las describimos mediante ecuaciones como la siguiente:
donde \(a, b\) son las partículas iniciales y \(c, d\) son las finales.
O en las desintegraciónes:
donde la partícula \(a\) se desintegra a las partículas \(b, \, c, \, d\)
En este caso aparecen 4 partículas en la interaccion o desintegración, pero pueden ser otro número.
Por ejemplo: $\( \alpha + \, {}^9\text{Be} \;\longrightarrow\; \,{} ^{12}\text{C} + \, n \\ n \to p \, + e + \bar{\nu}_e \)$
1.3.2. Sistema del laboratorio y centro de masas#
Las interacciones las referimos habitualmente a dos sistemas de referencia:
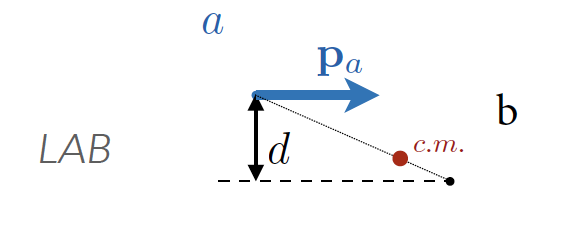
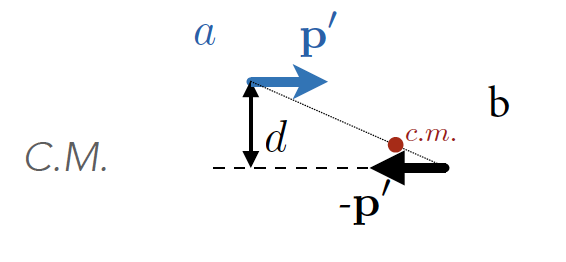
sistema del centro de masas (el suma de los momentos lineales de las partículas iniciales es cero)
sistema de laboratorio (una de las partículas iniciales está en reposo, típicamente \(b\)).
colisión en el centro de masas (izda) y en blanco fijo (derecha) de dos partículas \(a, \, b\). |
1.3.3. Cantidades continuas conservadas#
Sabemos por el teorema de M. Noether que por cada simetría continua que presenta un sistema físico se conserva una cantidad asociada.
En este caso para:
simetría temporal, conservación de la energía
simetría traslacional, conservación del momento lineal.
simetría rotacional, conservación del momento angular
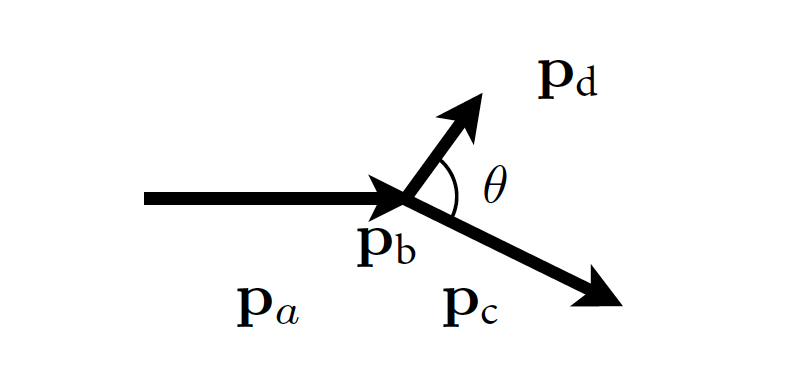
cuadrimomentos de la interacción (blanco fijo) [M. Caamaño] |
Por lo tanto tenemos:
La energía el momento lineal: $\( E_a + E_b = E_c + E_d \\ \mathrm{p}_a + \mathrm{p}_b = \mathrm{p}_c + \mathrm{p}_d \)$
Y damos la energía cinética, \(T\), como:
Definimos la energía de la interacción, \(a + b \to c + d\), o \(Q\) como la diferencia de masas iniciales y finales:
como la energía liberada tras la interacción (si \(Q>0\)) o la energía mínima necesaria para que la interacción puede tener lugar (si \(Q <0\)).
En el caso de la desintegraciones: \(a \to b + c + d\), para que tenga lugar debe cumplirse que:
Con la energía mínima \(Q\) las partículas se creen en reposo, sin movimiento, en el c.m.
En el caso del momento lineal se cumple que la suma de los momentos lineales antes y después de la interacción es la misma.
En el caso de que estemos en el entro de masa la suma de los momentos lineales antes y después es nula.
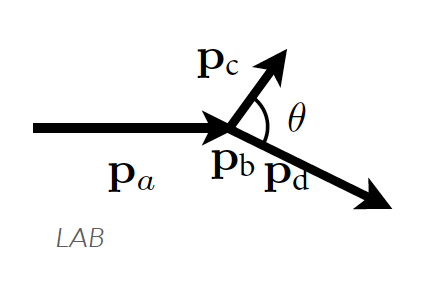
momento en el sis. lab |
¿Qué valor tiene \(\mathrm{p}_b\)? ¿Y \(\mathrm{p}'_b\)?
Es muy útil considerar cantidades invariantes Lorentz, que no dependan del sistema de coordenadas.
En particular en la iteracción \(a + b \to c+ d\) hay cuatro cuadrimomentos, los iniciales \(p_a, p_b\) y los finales \(p_c, p_d\), y podemos definir tres invariantes Lorentz llamados los invariantes de Mandelstam:
Veremos más adelante el significado y utilidad del invariante \(s\).
En particular en el caso de la conservación del momento angular debemos considera el espín de las partículas!
1.3.4. cantidades discretas#
En las interacciones se conservan determinadas cantidades aditivas:
la carga eléctrica
donde \(Q_i\) es la carga de cada partícula.
Y veremos que las interacciones se conservan diversos números cuánticos aditivos:
número leptónico
número bariónico
Lo que nos permite saber si una interacción se realiza o no en la Natureleza
Una de las propiedades que estudiaremos de las interacciones es su comportamiento frente a dos transformaciones discretas:
la conjugación de carga: cambiar partículas por antipartículas y viceversa. Esto es invertimos sus cargas y números cuánticos.
la inversión de paridad: cambiar el sistema de referencia \((t, {\bf x}) \to (t, -{\bf x})\)
En esféricas \((r, \theta, \phi) \to (r, \pi - \theta, \phi + \pi)\)
Veremos que tienen asociados unos números cuánticos multiplicativos.
En particular, la carga y la paridad se conservan en las interacciones electromagnéticas y fuertes, pero no en la débiles.
En concreto no se conserva paridad en la desintegración \(\beta\): \(n \to p + e + \bar{\nu}_e\)
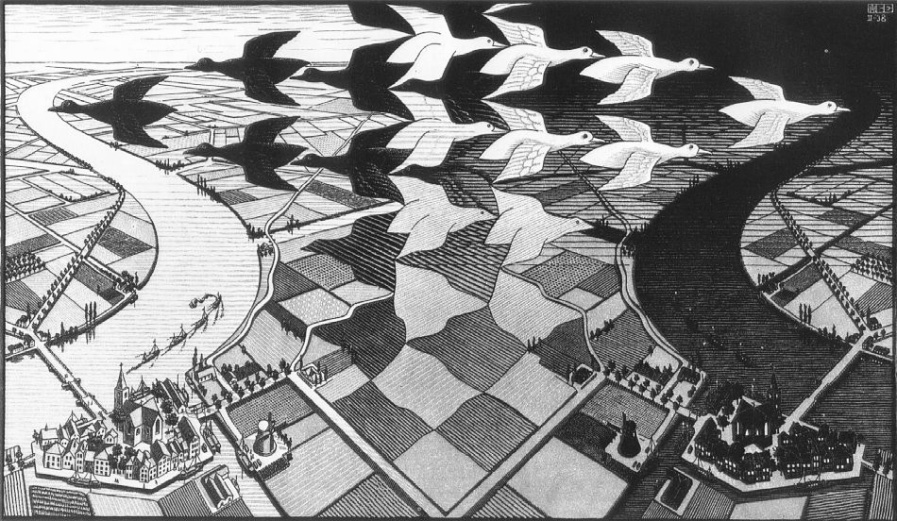
Podemos «ilustrar» la conjugación de carga e inversión de paridad con una imagen de Escher:
Frente a la paridad, clasificaremos las cantitades en:
escalares: \(X \to X\)
pseudo-escalares \(Y \to -Y\)
vectoriales: \({\bf V} \to -{\bf V}\)
pseudo-vectoriales \({\bf A} \to {\bf A}\)
1.4. Sección efifaz y tiempo de vida media#
1.4.1. Sección eficaz#
Una buena parte de los experimentos en Nuclear y Partículas son de dispersión: lanzamos partículas sonda contra un blando de otras partículas. Y estudiamos la dispersión de las partículas sonda \(a\) o las interacciones \(a + b \to c + d\).
ilustración de sección eficaz diferencial [M.Caamaño] |
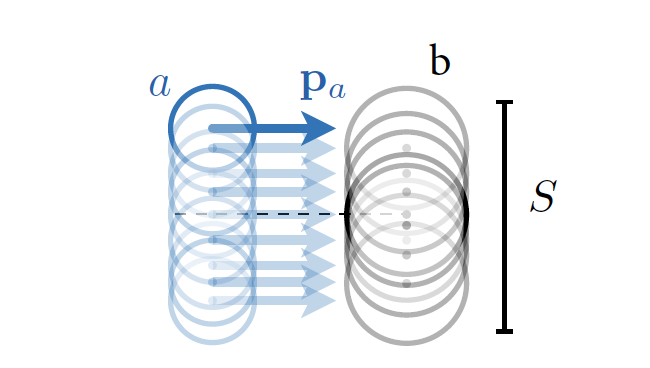
Para ello determinamos primero el número de interacciones por segundo que tienen lugar respecto al flujo de partículas sonda y de partículas blanco definimos la sección eficaz en el caso de experimentos en blanco fijo como:
donde \(\nu\) es el número de interacciones de un determiando tipo por segundo, \(a + b \to c + d\), \(N_b\) en número de partículas blanco, y \(\phi_a\) el flujo de partículas sonda, esto es \(N_a/S\), donde \(S\) el el área de exposición.
La sección eficaz tiene dimensiones de área \(\mathrm{m}^2\) y la unidad habitual es el barn \(b = 10^{-24}\, \mathrm{cm}^2\)
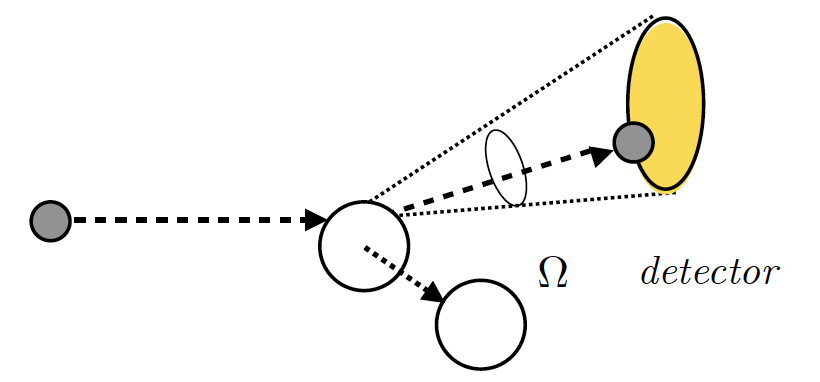
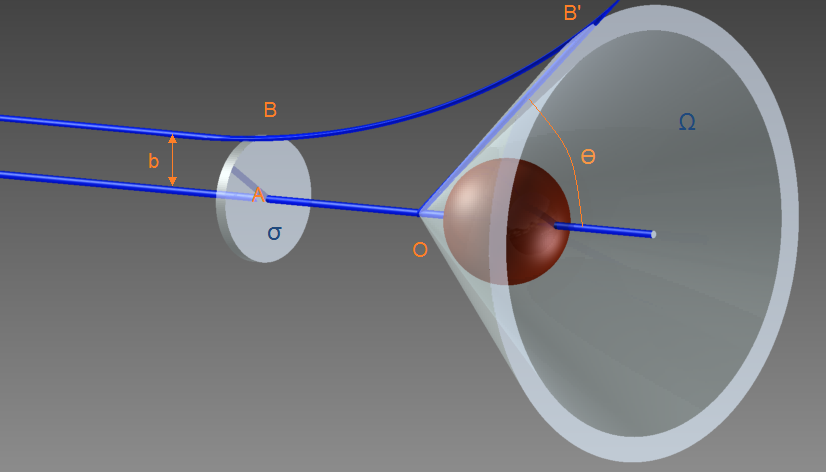
En muchas ocasiones, consderamos la sección eficaz diferencial respecto a la energía de la partícula sonda:
O respecto al ángulo de dispersión
ilustración de sección eficaz diferencial [M. Caamaño] |
[Wiki] |
1.4.1.1. blancos extensos#
¿Qué pasa si el blanco tienen un espesor \(d\), con una densidad \(\rho_b\) y masa atómica, \(M_B\)? ¿Cuánto se reduce el flujo de partículas inicial \(\phi_a\)?
Interacciones an blanco extenso [M. Caamaño] |
solución:
esto es:
donde:
que corresponde a la longitud de interacción.
1.4.2. Vida media#
Otro de los observables principales en Física Nuclear y de Partículas es el tiempo de desintegración.
Si consideramos la desintegración \(a \to b + c +d\), y disponemos de \(N_a\) partículas \(a\) independientes, en una unidad de tiempo esperamos que se produzcan un número de desintegracional proporcional a \(N_a\):
Las desintegraciones siguen una ley exponencial con una constante característica que llamamos tiempo de vida media, \(\tau\).
Por ejemplo, para la desintegración del neutrón, \(n \to p + e + \bar{\nu}_e\), el tiempo de vida es 878.4 s.
1.5. Radiación \(\alpha, \beta, \gamma\)#
1.5.1. De los griegos clásicos a nuestros días#
En el De Rerum Natura de Lucrecio (siglo I a.C.), el poeta romano, inspirado por Epicuro y en última instancia por Demócrito, expone una visión la visión de la Naturaleza:
todo lo que existe está hecho de átomos y vacío.
En nuestra visión contemporanea: el mundo está consitutido por partículas fundamentales y por vacío.
También argumenta que:
«Haud igitur redit ad nihilum res ulla, sed omnes dissoluuntur et in res cunctas remeare videntur.»
(Ninguna cosa vuelve a la nada: todas se disuelven y parecen regresar a otros cuerpos.)
En nuestra versión moderna: La energía ni se crea ni se destruye, se conserva. Las partículas se transforman unas en otras.
En la actualidad nuestro conocimiento de los componentes fundamentales de la Naturaleza está contenida en el Modelo Estándar
Clasificar y comprender las interacciones de las partículas es una tarea comunitaria que dura desde finales del siglo XIX, se inicial con el descubrimiento del electrón, y llega hasta nuestros días, siendo el último gran descubrimiento el del bosón de Higgs en 2012.
No obstante la imagen que surge del Modelo Estándard, aunque poco intuitiva, es relativamente simple.
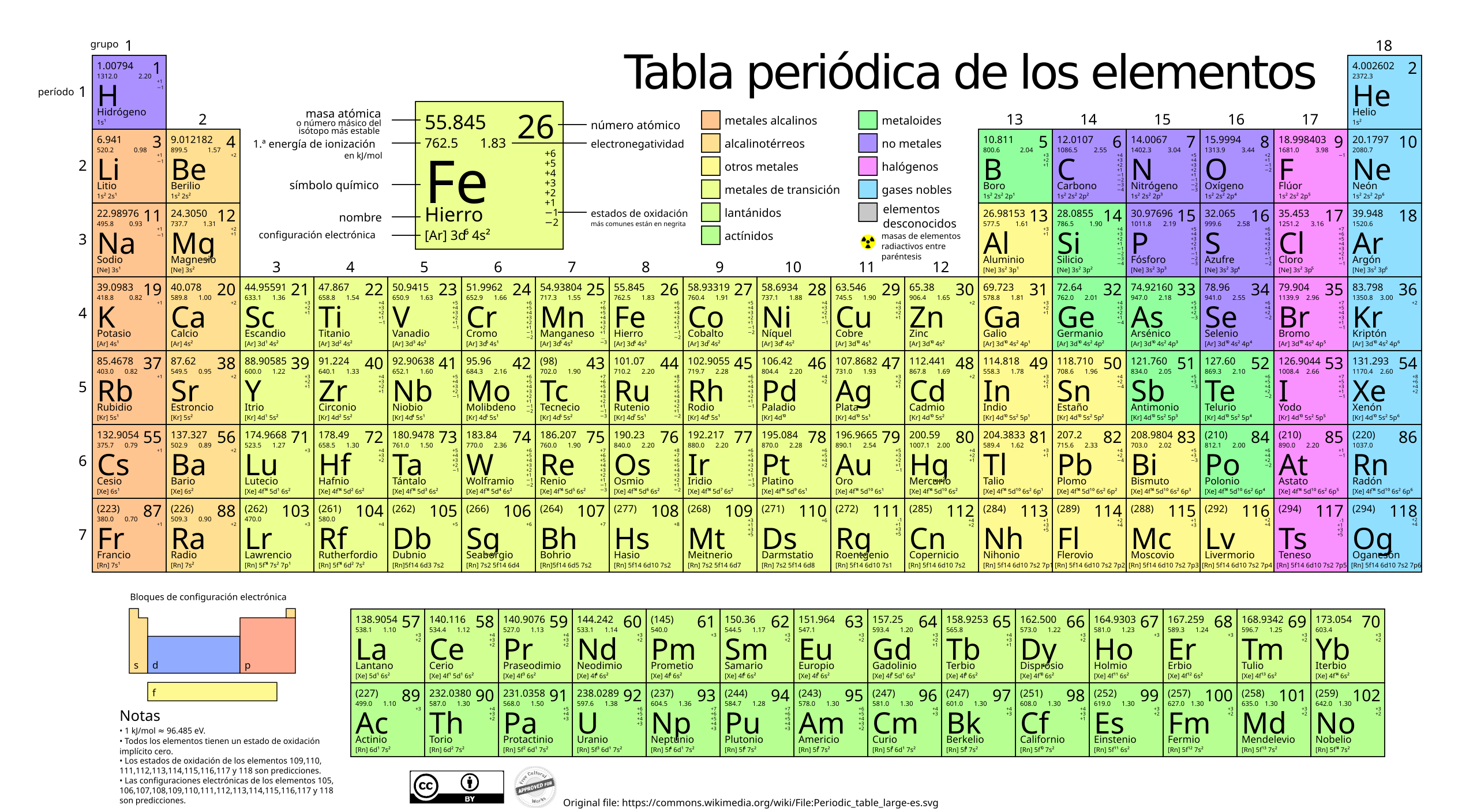
1.5.2. La tabla periódica#
Clasificar nos permite desvelar la estructura interna subyacente.
Mendeleev (1869) clasifica por propiedades los átomos y Moseley (1913) los ordena por Z.
Table periódica de los elementos Wikipedia |
La table periódica supone una ordenación de los elementos.
Disposición por número atómico (Z).
Periodos (filas) y grupos (columnas).
Bloques electrónicos: s, p, d, f.
1.5.3. Radiaciones α, β, γ#
A finales del siglo XIX y del siglo XX se descubrieron distintos tipos de radiaciones, cuyos nombres aún se utilizan: \(\alpha, \beta, \gamma\). Y que corresponden respectivamente a interacciones fuerte, débil y electromágnética.
Estas radiaciones tienen un rango típico de energía de MeV.
1.5.4. Radiación \(\alpha\)#
La radiación nuclear la descubrió (accidentalmente) Becquerel (1896) y la estudió en detalle Marie Curie.
Henri Becquerel, físico francés, estaba estudiando la fluorescencia de sales de uranio. Creía que, al exponerse al sol, éstas emitirían rayos X.
Un día nublado, sin sol, guardó sus placas fotográficas envueltas junto con el uranio. Cuando las reveló, vio que estaban veladas.
«Les sels d’uranium émettent spontanément des rayonnements capables d’impressionner une plaque photographique à travers un papier opaque.» (H. Becquerel)
El uranio emitía una radiación invisible, espontánea, sin necesidad de excitación externa. Eso fue el nacimiento del concepto de radiactividad natural.
Actualmente el becquerio se usa como unidad para indicar desintegraciones/segundo.
Posteriormente Maria Curie (Skłodowska) y su marido Pièrre Curie descubrieron dos nuevos elementos mucho más radiactivos que el uranio: Polonio y el Radio.
Marie acuñó el término “radioactividad”.
En esta desintegración del uranio se emite una radiación \(\alpha\), esto es un núcleo de helio (esto es con carga +2):
La radiación \(\alpha\) es poco penetrante.
1.5.5. radiación beta#
Se trata de la emisión por un núcleo de electrón, por ejemplo:
En 1899 Wilhelm Wien y Ernest Rutherford notan que algunas partículas emitidas de núcleos radiactivos son mucho más ligeras que las alfa y se comportan como electrones.
En 1913 James Chadwick estudia la dispersión de estas partículas y confirma que son electrones emitidos desde el núcleo.
La desintegración \(\beta\)
será nuestra guía para entender las desintegraciones débiles
La historia del neutrino merece su lugar aparte y la contaremos en otra ocasión.
1.5.6. radiación \(\gamma\)#
Finalmente, algunos núcleos emiten fotones de alta energía, penetrantes, que se denominan rayos \(\gamma\).
Como es el caso del Cobalto:
En 1900 y 1903 Ernest Rutherford y Paul Villard estudian la radiación del torio y del radio, notando que hay un componente extremadamente penetrante: lo llaman rayos gamma. Rutherford identifica que no son partículas cargadas (como \(\alpha\) o \(\beta\)), sino radiación electromagnética de alta energía.
Más adelante utilizaremos los diagramas de niveles para indicar las desintegraciones:
Diagrama de desintegración del \({}^{60}\mathrm{Co}\) [Wikipedia] |
Puedes explorar aquí otros diagramas de niveles
1.5.7. Interacciones electromagnética, débil y fuerte.#
Recordemos que la energía típica de las radiaciones nucleares \(\alpha, \beta, \gamma\) son del MeV.
La radiación \(\gamma\) es electromagnética, tiene referente clásico.
La desintegración \(\beta\) es débil, tiene un rago muy pequeño \(10^{-3}\) fm (fm = \(10^{-15}\)m), y aparece por primera vez en la reacciones nucleares. Su tratamiento es cuántico.
La desintegración \(\alpha\) es una manifestación de la interacción fuerte, la responsable de la existencia del núcleo, entre otros fenómenos, y su alcance es del fm. De nuevo su tratamiento es cuántico.
En Física Nuclear haremos un tratamiento cuántico y -en general- no relativista, mientras que en Física de Partículas, el tratamiento es cuántico y -casi siempre- relativista.
1.6. De los nucleos a los quarks#
1.6.1. Dispersión del núcleo#
En 1909, H. Geiger and E. Marsden estudiaban la dispersión de partículas alfa en una lámina de oro, y E. Rutherford sugerió estudiar si existían dispersiones a altos ángulos.
Esquema de dispersión [Geiger, Marsen] |
Rutherford: “It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.”
Rutherford concluyó, entre otras cosas, que la mayor parte de la masa y la carga positiva del átomo se concentran en una región extremadamente pequeña, a lo que se denominó núcleo.
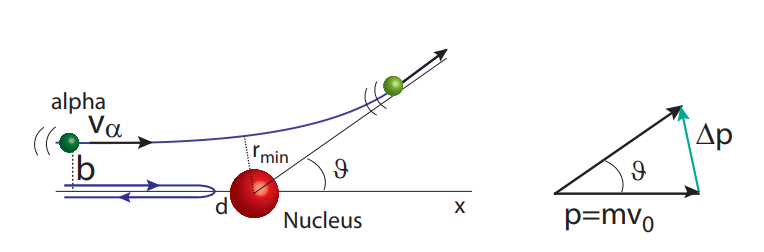
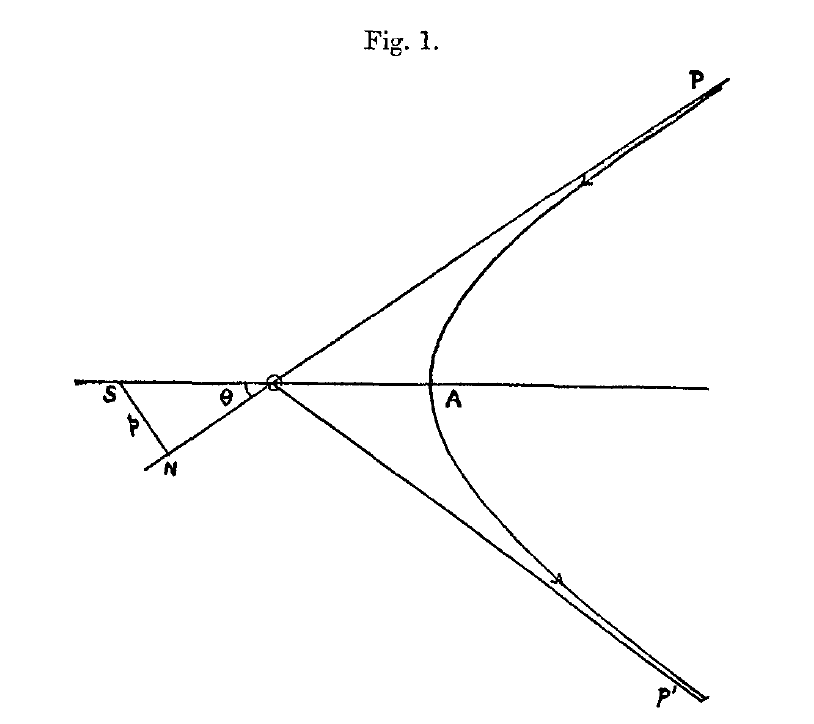
Dispersión hipérbola [Rutherford] |
Rutherford describió la dispersión de las partículas alfa a través de la interacción electromagnética. Asumiendo que el núcleo no tenía retroceso e ignorando la interacción con los electrones, la situación es matemáticamente la misma que las soluciones de Kepler a las órbitas planetarias: la partícula alfa recorre una hipérbola
Dispersión [Rutherford] |
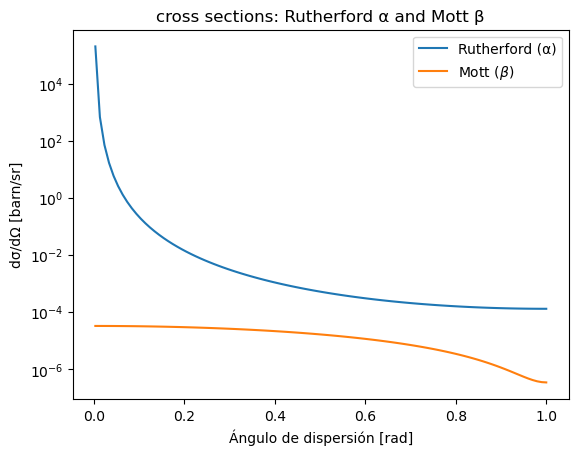
1.6.2. Dispersión de Mott#
Mott estudió la dispersión de electrones de alta energía en los núcleos, para ello hay que tener en cuenta el espín del electrón y la mecánica cuántica relativista.
Y si consideramos el retroceso del núcleo:
donde:
\(Z\): número atómico del núcleo
\(E\): energía total del electrón incidente
\(M\): masa del núcleo
\(\theta\): ángulo de dispersión en el laboratorio
import numpy as np
import matplotlib.pyplot as plt
from scipy import constants as const
# --------------------------------------------------
# 1) Dispersión de Rutherford
def sigma_rutherford(Z1, Z2, E, theta):
"""
Sección eficaz diferencial de Rutherford
Z1: carga de la partícula incidente
Z2: carga del núcleo
E: energía cinética [J]
theta: ángulo de dispersión [rad]
"""
factor = (Z1 * Z2 * const.e**2 / (16 * np.pi * const.epsilon_0 * E))**2
return factor / (np.sin(theta/2)**4)
# --------------------------------------------------
# 2) Dispersión de Mott con retroceso del núcleo
def sigma_mott(Z, E, M, theta):
"""
Sección eficaz diferencial de Mott con recoil
Z: número atómico del blanco
E: energía del electrón incidente [J]
M: masa del núcleo [kg]
theta: ángulo de dispersión [rad]
"""
# energía del electrón dispersado considerando retroceso
E_prime = E / (1 + (2*E/(M*const.c**2)) * np.sin(theta/2)**2)
# corrección relativista por espín (aproximada)
beta = np.sqrt(1 - (const.m_e * const.c**2 / E)**2)
factor = (Z * const.e**2 / (16 * np.pi * const.epsilon_0 * E))**2
return factor * (E_prime / E) * (1 - beta**2 * np.sin(theta/2)**2)
# --------------------------------------------------
#
def plot_cross_sections(E_alpha = 5e6, E_electron = 5e6, M_nucleus = 197):
theta = np.linspace(0.01, np.pi, 100)
E_alpha *= const.e # MeV en julios
E_electron *= const.e # MeV en julios
M_nucleus *= const.u # masa en kg (1 u = 1.660539e-27 kg)
sigma_R = sigma_rutherford(2, 79, E_alpha, theta)
sigma_M = sigma_mott(79, E_electron, M_nucleus, theta)
barn = 1e-24 # 1 barn en m²
plt.plot(theta/np.pi, sigma_R/barn, label='Rutherford (α)')
plt.plot(theta/np.pi, sigma_M/barn, label=r'Mott ($\beta$)')
plt.yscale('log')
plt.xlabel('Ángulo de dispersión [rad]')
plt.ylabel('dσ/dΩ [barn/sr]')
plt.title('cross sections: Rutherford α and Mott β')
plt.legend()
plt.show()
# Energy in eV, Mass in amu
plot_cross_sections(E_alpha = 5e6, E_electron = 5e6, M_nucleus = 197)
1.6.3. Descubrimiento del protón#
Fue Ernest Rutherford, en 1917, identificó el protón. Al borbardear nitrógeno con partículas alfa observó que en la colisión aparecía una partícula más ligera que la alfa, con la misma carga positiva pero de masa mucho menor.
En 1919, Rutherfod concluyó que el núcleo del hidrógeno era un constituyente fundamental de la materia, presente en todos los núcleos atómicos. Así nació el concepto de protón como partícula elemental de carga positiva.
Permitió entender que todos los núcleos podían concebirse como combinaciones de protones (y más tarde neutrones, tras su descubrimiento en 1932).
Abrió la puerta a la idea de transmutaciones nucleares: un elemento podía convertirse en otro.
1.6.4. Descibrimiento del neutrón#
El modelo nuclear de Rutherford planteaba que los núcleos estaban compuestos únicamente de protones, pero la masa de los núcleos era mayor de lo que explicaba el número de protones.
Por ejemplo, el núcleo de helio debía tener masa ~4 amu, pero con 2 protones y 2 electrones (como se especulaba) no cuadraba. Faltaba “algo” en el núcleo.
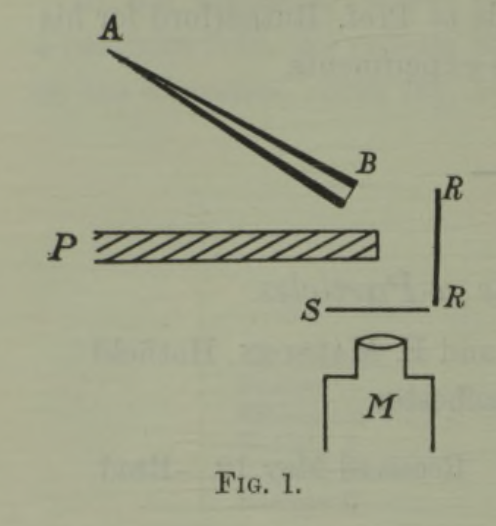
En 1930, Walther Bothe y Herbert Becker bombardearon berilio con partículas alfa y detectaron una radiación muy penetrante, más que los rayos gamma. Al principio se pensó que era radiación gamma de alta energía.
James Chadwick, en el laboratorio Cavendish (Cambridge), estudió con detalle esa radiación: Usó como blanco el berilio:
Esa radiación impactaba en parafina (rica en protones), expulsando protones de la cera. Si fueran fotones gamma, la energía necesaria para expulsar protones sería enorme, Concluyó que la radiación no eran fotones, sino partículas neutras de masa comparable a la del protón. Chadwick llamó a estas partículas neutrones.
De esta forma los núcleos estaban formados por protones y neutrones (llamados ambos nucleones).
Explicó por qué los núcleos no explotaban electrostáticamente: los neutrones añadían masa y la fuerza fuerte es la que ligua los nucleones en el núcleo.
1.6.5. Los cuatro magníficos#
La Naturaleza está formada por átomos eléctricamente neutros formados por un núcleo masivo y electrones en capas. El núcleo está formado por protones (asociado con el número atómico \(Z\)) y neutrones (que conjuntamente dan el número másico \(A\)). Los electrones solo aportan del orden del 0.1 % de la masa del átomo.
El átomo está vacío, los núcloes tiene un tamaño del orde del 1-10 fm (fm = \(10^{-15}\) m), mientras que el átomo tiene \(10^{-10}\) m, esto es, entre ambos ¡hay un factor \(10^5\)!
Así pues en primera aproximación la Naturaleza está compuesta por:
Además del neutrino, \(\nu\), que aparece en la desintegración \(\beta\)
Esto es la materia del Universo está compuesta por 4 partículas «fundamentales»:
Está visión del mundo construido con \(p, n, e\) duró solo 100 días ¡hasta que se descubrió el positrón!
1.6.6. Dispersión de electrones a alta energía.#
En la década de los 50’s Hofstadter realizó una serie de experimentos con el acelerador Mark III en Stanford (California, EEUU) de dispersión de núcleos con electrones de muy alta energía (100 MeV). Y descubrió que los electrones exploraban la estructura nuclear al penetrar dentro del núcleo. Acuñó el tamaño de fermi (fm = \(10^{-15}\) m) y estableció que el núcleo no es una bola rígida.
Diagerama de la dispersión de Hofstadler |
Holfstadter verificó que la dispersión de Mott se modifica por un factor, llamado de forma, \(F(q^2)\)
donde
siendo \(p, \; p'\) el cuadrimomento inicial y final del electrón. A \(q\) se le llama cuadrimomento transferido.
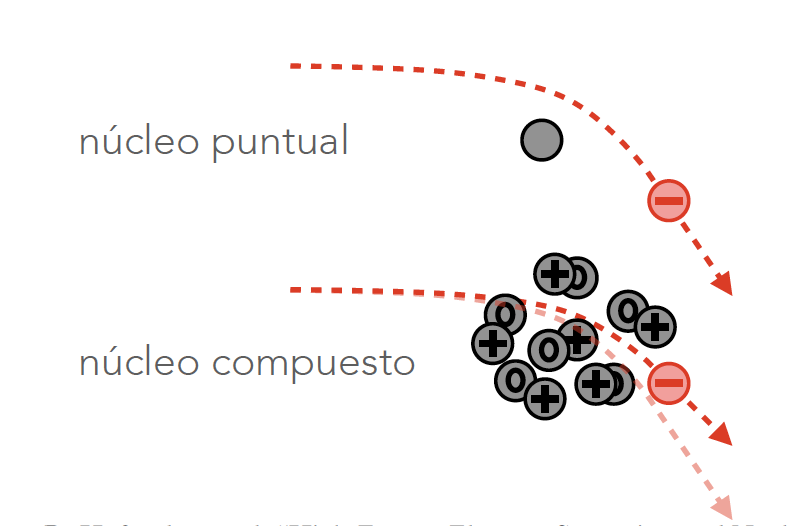
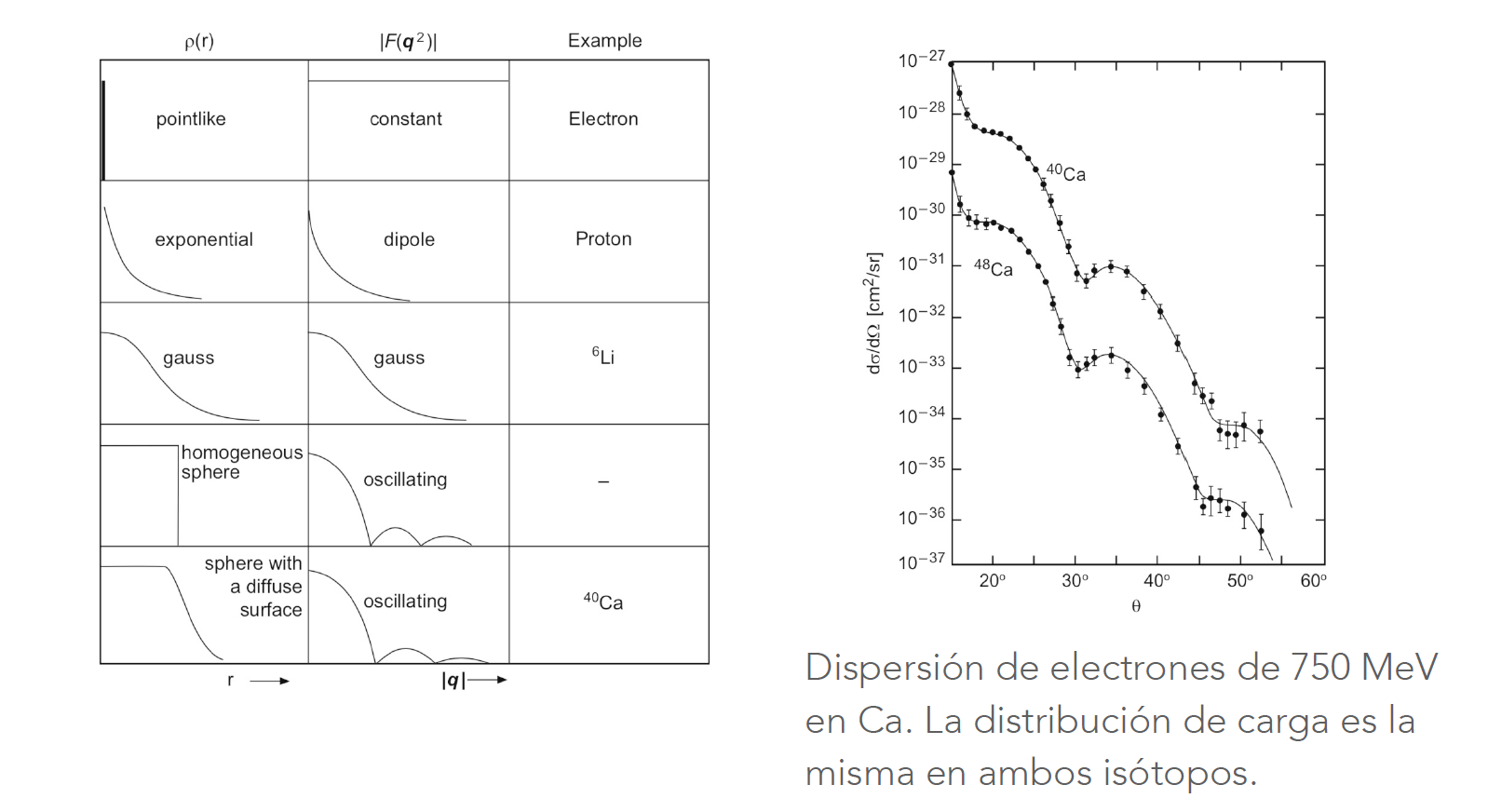
Este factor de forma, como veremos en la parte de Nuclear, depende de la estructura del núcleo:
Factores de forma [M. Caamaño] |
1.6.7. Three quark for the Muster Mark!#
En la década de los 60 usando electrones de más alta energía se pudo explorar el interior de los propios nucleones.
Así, la distribuciones de forma mostraban patrones que coincidían con la posible existencia de partículas puntuales en el interior de los nucleones. R. Feynman los llamó partones.
Los conocemos como quarks. El término fue introducido por Murray Gell-Mann en 1964 cuando propuso su modelo de “quarks” para explicar la estructura de los hadrones (protones, neutrones, mesones), que tomó el nombre de la novela “Finnegans Wake” (1939) de James Joyce, un libro experimental y casi impenetrable, famoso por su lenguaje inventivo. Gell-Mann creía que los quarks era solo una herramienta matemática para explicar la composición de las partículas llamadas hadrones descubiertas hasta la fecha
De forma simultánea, George Zweig en el CERN también propuso un modelo de constituyentes internos para los hadrones. Él los llamó “aces” (como los ases de una baraja). Él si creía que eran reales.
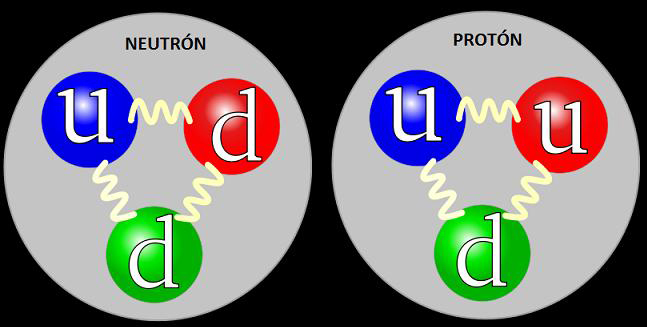
Actualmente decimos que el protón y el neutrón están formados por quarks.
El quark up (\(u\)) con carga \(2|e|/3\) y el quark down (\(d\)) con carga \(-1|e|/3\).
De tal forma cada nucleón esta compuesto por tres quarks mediante la fuerza fuerte y cuya carga entera:
Estructura del protón y del neutrón [Wikipedia] |
1.6.8. Los cuatro y su compañía#
Las cuatro partículas fundamentales son:
Pero la Naturaleza es más diversa:
además de las partículas, existen las antipartículas, que tiene las cargas opuestas a las partículas, por ejemplo el positrón, \(e^+\)
existen partículas como otros leptones (que se comportan como el electrón) y los hadrones (que están formados por quarks) y que son inestables.
Clasificar y ordenar las partículas en la tabla de partículas del Modelo Estándar supuso un reto durante más de 40 años.
1.7. Introducción al modelo estandar#
EL modelo estandar (SM) de Física de Partículas es uno de los grandes logros de la Física (a pesar de su pobre nombre).
El Modelo clasifica todas partículas elementales y establece las interacciones entre ellas.
El Particle Data Group (PDG) es un grupo de trabajo que se encarga de recopilar y publicar toda la información relevante sobre física de partículas. Puedes consultar su página donde está toda la información.
En esta sección veremos brevemente cómo se clasifican las partículas y sus características principales.
Hasta donde sabemos la Naturaleza está compuesta de 12 partículas que forman la materia, que llamamos fermiones, 12 bosones que transmiten la fuerzas y una última, el bosón de Higgs, que les otorga las masas.
Aunque la materia ordinaria, y la mayoría del Universo, está formada por 4 partículas de materia. Esencialmente el protón, el neutrón, el electrón y el neutrino. De ellas son estables el protón, el electrón y el neutrino.
El resto de partículas jugaron un papel relevante durante los primeros segundos del Universo. En la actualidad, se producen principalmente en los experimentos, y son, con excepción del neutrino, inestables y se desintegran.
Junto a las partículas tenemos sus antipartículas, que a pesar de su nombre, son igual a las partículas pero con sus cargas opuestas.
Las antipartículas aparecen en condición de igualdad y de forma complementaria a las partículas en las ecuaciones de la teoría. Sin embargo, el Universo actual está prácticamente formado por materia. No sabemos qué ocurrió en los primeros segundos del Universo que provocó que sobreviviese solamente la materia.
En cuanto a las fuerzas, sabemos que hay 3 interacciones principales:
la electromagnética, mediada por el fotón.
la débil, mediada, cuando se produce cambio de carga eléctrica, por los bosones vectoriales, \(W^\pm\), (donde el signo hace referencia a la carga), y las que no cambian la carga eléctrica, mediadas por el \(Z\)
la fuerte fundamental, mediada por los gluones. La fuerza responsable de la estabilidad y dinámica de los núcleos, es una fuerza fuerte residual. Similar al papel que juega el electromagnetismo en la formación de moléculas.
Finalmente, la masa, que en principio es una propiedad de la partícula, es en realidad la consecuencia de la interacción de la partícula con el bosón de Higgs. Cuanto más masa tiene una partícula, más fuerte interacciona con el bosón de Higgs.
1.7.1. El SM a simple vista#
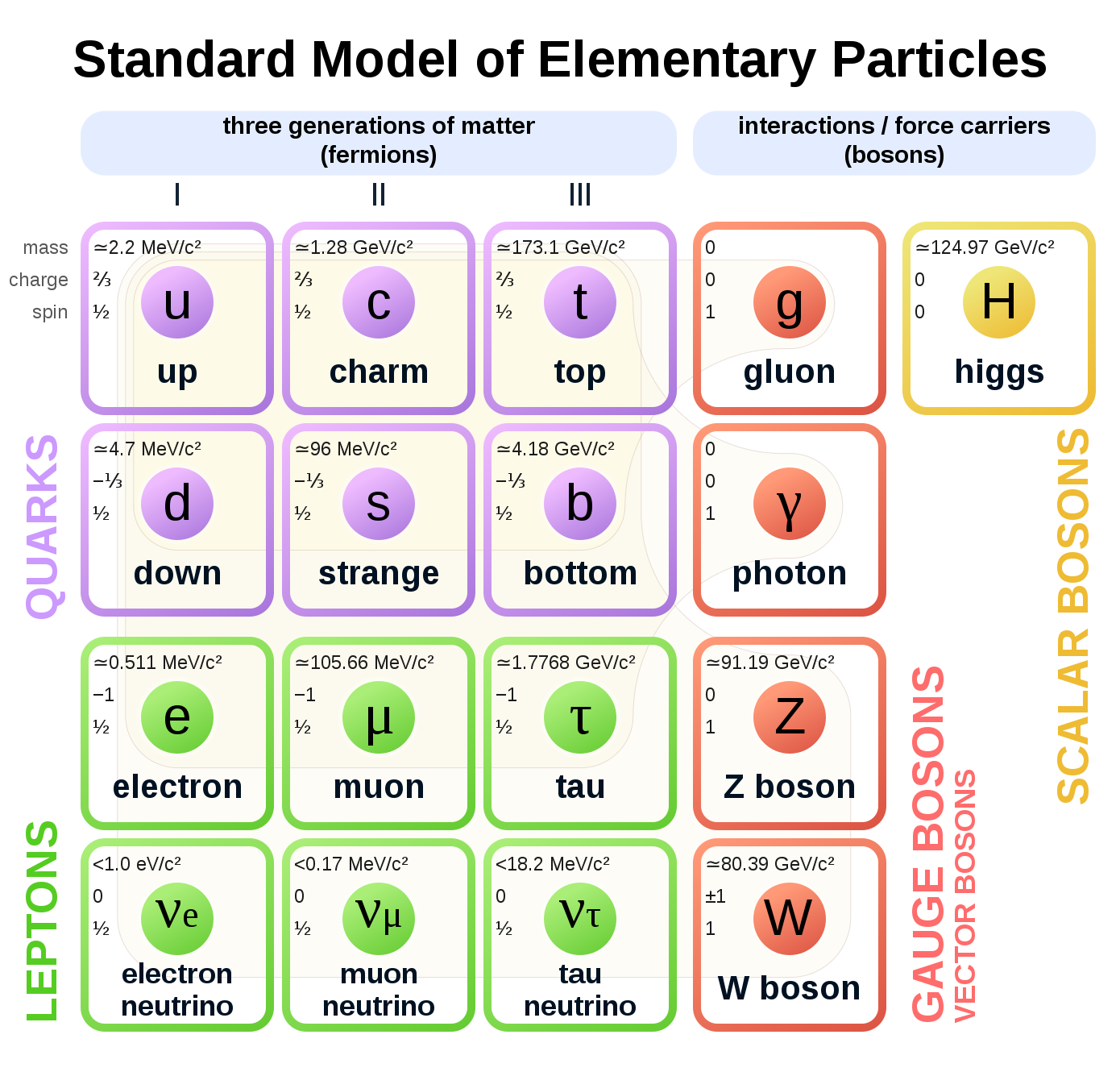
La siguiente tabla muestra las partículas fundamentales y sus propiedades principales:
Las partículas del modelo estandar |
La materia está formada por los fermiones, que son partículas elementales de spín \(1/2\).
Los bosones vectoriales, con spín \(1\), son los mediadores de las fuerzas fuerte, débil y electromagnética.
El bosón scalar de Higgs, que tiene spín 0, dota de masas a los fermiones y a los bosones vectoriales de la fuerza débil.
1.7.2. Fermiones#
Los fermiones son las partículas que constituyen la materia, tienen spín \(1/2\) y obedecen a la ecuación de Dirac.
Los fermiones obedecen a la estadística de Fermi, por ello no encontramos dos fermiones en un mismo estado, de ahí que formen los componentes, los bloques, de la materia.
Los fermiones se dividen en:
quarks : si interaccionan fuertemente
leptones: si no interaccionan fuertemente
fuerte |
electromagnética |
débil |
|---|---|---|
quarks |
quarks y leptones cargados |
quarks y leptones |
1.7.2.1. las anti-partículas#
Sabemos que los fermiones se rigen por la ecuación de Dirac, y se describen con un nuevo objeto matemático, los espinores de Dirac.
Fue Dirac quien a partir de su famosa ecuación, propuso que cada partícula, tiene su anti-partícula. La diferencia entre ellas son las cargas. Las antipartículas tienen las cargas opuestas a la partícula, pero tienen la misma masa, espín y vida media.
Si \(f\) es un fermión, denotamos \(\bar{f}\) como su antifermión, aunque para los antileptones, que tienen carga eléctrica (+), los llamaremos simplemente: \(e^+, \mu^+, \tau^+\).
1.7.2.2. generaciones#
Por alguna razón que desconocemos, existen tres generaciones o familias idénticas de partículas, que son una copia con más masa, de la primera familia. Pero sí sabemos que solo hay 3 familias.
Decimos que los fermiones (tanto leptones como quarks) aparecen en tres generaciones o familias.
En cada generación, tanto leptones como quarks, se agrupan en dupletes con posiciones arriba y abajo.
Decimos que las tres generaciones de leptones se comportan con universalidad (de igual manera) frente a las interacciones si se tiene en cuenta que sus masas son diferentes.
Decimos también que las partículas tienen sabor, que en realidad se corresponde con la identidad de la partícula. Por ejemplo decimos que el quark s tiene extrañeza, el quark b, belleza, el neutrino electrónico tiene sabor electrónico. Y para los leptones cargados, decimos un leptón cargado de sabor electrónico, para referirnos al electrón.
Las partículas desde el punto de la interacción débil no se corresponden exactamente con las partículas de masa, en otras palabras, la interacción con los campos vectoriales no está alineada con la interacción con el bosón de Higgs. Lo que da lugar a una física compleja y muy rica, que se conoce como física del sabor. Un ejemplo de esta física son las oscilaciones de neutrinos.
La siguiente tabla muestra los fermiones agrupados por familias, su carga eléctrica y las fuerzas que sienten:
1 |
2 |
3 |
Q (e) |
fuerte |
electromag. |
débil |
Higgs |
|
|---|---|---|---|---|---|---|---|---|
quarks |
u |
c |
t |
\(\frac{2}{3}\) |
sí |
sí |
sí |
sí |
d |
s |
b |
\(-\frac{1}{3}\) |
sí |
sí |
sí |
sí |
|
leptons |
\(\nu_e\) |
\(\nu_\mu\) |
\(\nu_\tau\) |
0 |
no |
no |
sí |
? |
\(e\) |
\(\mu\) |
\(\tau\) |
-1 |
no |
sí |
sí |
sí |
La carga eléctrica depende de su posición en el duplete. El fermión de arriba tiene una carga \(+1\) comparada con la del de abajo.
La siguiente tabla muestra la masa de los fermiones
u (2 MeV) |
c (1.2 GeV) |
t (170 GeV) |
d (5 MeV) |
s (93 MeV) |
b (4.2 GeV) |
\(\nu_e\) (< eV) |
\(\nu_\mu\) (< eV) |
\(\nu_\tau\) (<eV) |
\(e\) (511 keV) |
\(\mu\) (106 MeV) |
\(\tau\) (1.77 GeV) |
Podemos notar que el quark top es extremadamente pesado, mientras que el neutrino, del que no sabemos su masa es extraordinariamente ligero, del orden de \(10^6\) veces más ligero que el electrón.
De las dos tablas anteriores vemos que el neutrino es particular, diferente, solo interacciona débilmente. Veremos a lo largo de estas clases como el neutrino ejemplifica muy bien las características fundamentales del Modelo Estándar, además, hoy en día oculta todavía varios misterios por resolver, como si es o no su propia antiparticula o como interacciona con el bosón de Higgs.
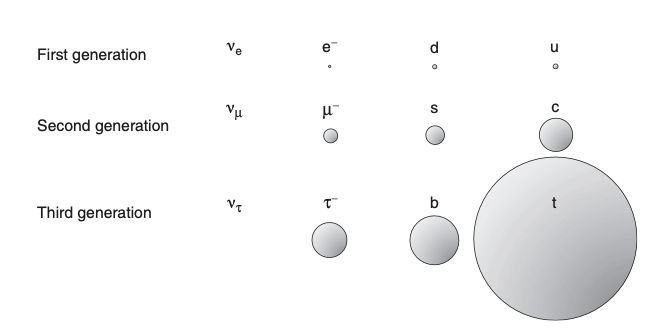
La siguiente figura muestra de forma gráfica la disparidad de masas entre los fermiones:
Masas de los fermiones [MT1.1] |
No sabemos por qué los fermiones tienen este patrón de masas, que al final, equivale a decir que no sabemos por qué se acoplan al bosón de Higgs de forma tan dispar.
Puede que necesitamos conocer mejor la física de Higgs para entender el origen de los valores de las masas de los fermiones.
1.7.3. Leptones#
Las tres familias de leptones son:
Los leptones cargados \(\mu, \tau\) son una copia con más masa del \(e\).
En la Naturaleza, hasta la fecha, hemos verificado que las interacciones conservan el número leptónico, \(L\), que es el número de leptones menos el de anti-leptones.
Por ejemplo en la desintegración \(\beta\):
El número leptónico antes y después de de la desintegración es \(L = 0\). Dado que \(e\) es un leptón, \(L = +1\) y \(\bar{\nu}_e\) un anti-lepton, \(L=-1\).
Por lo tanto el neutrino, que es el leptón más ligero, es estable.
Por supuesto, todas las interacciones conservan la energía, el momento lineal y angular, y la carga eléctrica.
Los leptones cargados se desintegran via las interacciones débiles.
La siguiente tabla muestras sus vidas medias:
\(e\) |
——— \(\mu\) ——— |
——- \(\tau\) —- |
|---|---|---|
estable |
\(2.6 \, 10^{-6}\) s |
\(2.9 \, 10^{-13}\) s |
El electrón es estable, porque todas las interacciones conservan la carga eléctrica, y es el leptón cargado más ligero.
Los muones de 10 GeV, recorren habitualmente unos metros antes de desintegrarse.
Mientras que los tauones se desintegran al poco de ser producidos, a 45 GeV por ejemplo a recorren unos mm.
Existen tres neutrinos de sabor, \(\nu_e, \nu_\mu, \nu_\tau\) asociados a sus parejas leptónicas \(e, \mu, \tau\) respectivamente.
El SM postulaba que no tienen masa, pero gracias a los experimentos de oscilaciones de neutrinos sabemos que tienen masa.
Su masa se desconoce pero es muy pequeña \(\lt 1\) eV, a comparar con los 511 keV del electrón.
Los neutrinos no tienen carga eléctrica, tienen una masa muy pequeña, son estables, y sólo interactuan débilmente. ¡Son muy cool! Solo hace falta ver las tablas anteriores para dease cuenta.
Son los leptones más peculiares del SM y que tengan masa es la única prueba hasta el momento de que el SM es incompleto o incorrecto.
Las características de los leptones y las peculiaridades de la desintegración débil y de los neutrinos las estudiaremos en el [Tema-leptones].
1.7.4. Los quarks#
Las tres generaciones de quarks son:
Los quarks \((c, s)\), encanto y extrañeza respectivamente, y \((t, b)\), top y bottom (o belleza), son copias con más masa del par \((u, d)\), arriba y abajo.
Los quarks \(u, d, s\) son ligeros, los quark \(c, b\) son pesados. El top, \(t\), es incluso más pesado que los bosones vectoriales \(W^\pm, Z\) y no llega a producir hadrones. Esta diferencia hará que la física de los hadrones formados por quark ligeros y pesados sea diferente.
Los quarks tienen carga fraccionaria: los de arriba \(+2/3\) y los de abajo \(-1/3\) en unidades de \(e\). No hay nada extraño en que la carga sea fraccionaria. Debemos a uno de los padres de la constitución americana, B. Flanklin, que el electrón se defina como carga eléctrica negativa, pero eso es solo una convención.
Los quarks no son libres, sólo aparecen en partíclas compuestas, los hadrones. Este fenómeno se conoce como confinamiento.
Si los quarks fueran partículas libres, los habríamos detectado facilmente, ya que en presencia de un campo magnético, sus trayectorias se curvarían de acuerdo a su carga.
Todavía no tenemos una explicación exacta del confinamiento de los quarks, pero la teoría que rigue las interacciones fuertes, la cromodinámica cuántica, QCD, permite una explicación.
Los quarks aparecen con tres cargas fuertes o de color, que se denominan: rojo, verde y azul, \(r, g, b\). Y por supuesto no tiene nada que ver con los colores habituales.
Esto es, un mismo quark existe en tres colores, por ejemplo el quark belleza, \(b\), puede ser rojo, verde o azul. Esto quiere decir que en realidad no tenemos 6 quarks sino 18. Decimos que cada quark de sabor se presenta en tres colores (no solo hay simetría en física, a veces, también hay poesía).
Para cada color existe también su anti-color, esto es anti-rojo, anti-verde o anti-azul, que viene asociado a los anti-quarks.
Sin embargo, la QCD exige que los únicos hadrones reales sean neutros al color, digamos que son descoloridos o blancos, de forma similar al hecho de que los átomos son eléctricamente neutros.
Estudiaremos los quarks, los hadrones y el color en el [Tema-quarks].
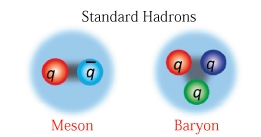
Sólo hay dos posibilidades de combinación de quarks para que los hadrones sean incoloros, o bien mediante una combinación de tres quarks (o antiquarks), cada uno con un color, lo que llamamos barión (o antibarión), o un mesón, formado por un quark y un antiquark con colores complementarios (por ejemplo, rojo y anti-rojo)
Los hadrones se clasifican en.
bariones, formados por tres quarks.
mesones, formados por un par quark y antiquark.
Imagen esquemática de un mesón y un barión |
Con estas dos posibilidades, la carga eléctrica de los hadrones es entera.
El protón y el neutrón son bariones. El protón está formado por el trío de quarks de valencia (\(uud\)), cuya carga es \(+e\), y el neutrón por (\(udd\)), cuya carga es nula.
También, en la Naturaleza, hasta le fecha, hemos comprobado que se conserva el número de quarks, decimos que se conserva el número bariónico, \(B\), (el número de bariones menos el de antibariones).
Notar que los mesones tienen número de quarks nulo porque son la combinación de un quark y un antiquark. Así que en vez de contar quarks contamos bariones en las interacciones.
Por ejemplo, de nuevo, en la desintegración \(\beta\):
A ambos lados de la interacción el número bariónico es 1. El \(p\) y el \(n\) tienen los dos \(B = 1\)
Como el protón, que es el barión más ligero, es estable.
Remarquemos que la desintegración \(\beta\)
y el resto de interacciones conservan:
la carga eléctrica, \(Q\),
el número leptónico, \(L\),
el número bariónico, \(B\).
La anterior desintegración es posible energéticamente, porque el \(n\) tiene una masa (939 MeV) ligeramente superior al \(p\) (938.3 MeV). De esa pequeña diferencia proviene que la vida media del neutrón sea aproximadamente de 14 mins.
Dado que la partícula estable de los leptones es el \(e\) y de los bariones el \(p\). La conservación del número leptónico y bariónico, a igualdad del número de ambas partículas, nos asegura que el Universo sea eléctricamente neutro.
Muy diferente sería si la Naturaleza si el neutrino hubiese sido una partícula masiva con posibilidad de desintegrarse, o si el protón tuviera más masa que el neutrón.
El resto de hadrones, (ya sean mesones o bariones), así como leptones cargados \(\mu, \tau\), se desintegran:
La vida media de la desintegración depende de:
del tipo de desintegración permitida, ya sea ésta fuerte (via gluones), electromagnética (via un fotón) o débil (vía bosones \(W^\pm\)).
del espacio fásico permitido. A mayor diferencia de masas entre la partícula madre y las hijas más espacio fásico.
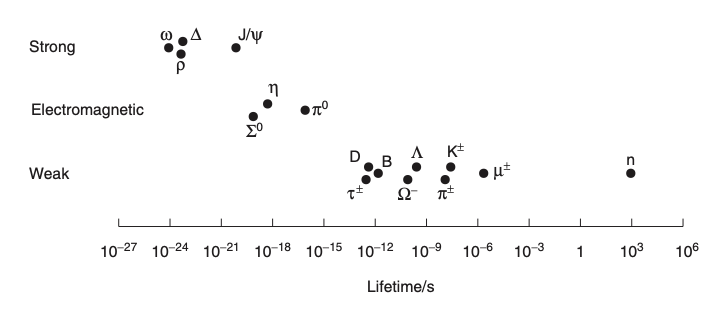
La figura muestra la vida media de varias partículas y su tipo de desintegración.
Vida media de algunas partículas dependiendo del tipo de desintegración [MT1.1] |
La partículas que se desintegran débilmente son aquellas con una vida media «mayor».
cuestión: ¿Por qué la vida media del \(n\) es tan alta?
1.7.5. Los mediadores de las fuerzas#
Recordemos que la fuerzas son responsables entre otros fenómenos de:
la electromagnética, de la estabilidad y complejidad de los átomos
la débil, de las desintegraciones \(\beta\) nucleares.
la fuerte, de la estabilidad y complejidad de los núcleos (protones y neutrones) y de los hadrones.
1.7.5.1. Propiedades de los portadores#
Describimos las interacciones de las partículas como el intercambio de un mediador o portador de la fuerza entre ellas.
Cada portador interviene según la carga (por ejemplo eléctrica o color) de los fermiones a los que interacciona.
Los portadores son bosones vectoriales (spín 1) y obedecen la ecuación de Maxwell.
En la tabla se muestra la intensidad aproximada de las distintas fuerzas, su carga eléctrica y su masa:
fuerza |
intensidad |
bosón |
Q (e) |
masa (GeV) |
|---|---|---|---|---|
fuerte |
1 |
\(g\) (gluón) |
0 |
0 |
electromagnetismo |
\(10^{-3}\) |
\(\gamma\) (fotón) |
0 |
0 |
débil |
\(10^{-8}\) |
\(W^{\pm}\) |
\(\pm1\) |
80.4 |
\(Z^0\) |
0 |
91.2 |
||
gravedad |
\(10^{-37}\) |
El fotón carece de masa, es el responsable de las interacciones electromagnéticas, y éstas tienen rango infinito, lo que está relacionado con su masa.
Sin embargo, los bosones vectoriales débiles, \(W^\pm, Z^0\), tiene una masa elevada \(80\) y \(91\) GeV respectivamente, y su alcance es puntual.
Fue Yukawa quien para explicar la fuerza que mantenía los nucleones en el interior del núcleo, sugirió un potencial que decayera exponencialmente a partir de un radio típico, (el fm). Asociado a ese potencial debía existir una partícula masiva (200 MeV), el pión, que cuyo alcance de acción estuviera en ese rango de distancia del nucleón.
Las interacciones débiles, mediadas por portadores muy masivos, tienen, en la interpretación de Yukawa, un rango puntual.
A la escala de masa de los portadores débiles la llamamos escala electrodébil, \(\mathcal{O}(100)\) GeV, que corresonde a una interacción puntual de \(10^{-18}\) m.
Los bosones \(W^\pm\) son cargados eléctricamente. En las interacciones que median trasportan consigo una carga eléctrica (\(\pm\)). Por eso sus interacciones se conocen también, por abuso del lenguaje, como corrientes cargadas (CC).
Las interacciones del bosón \(Z^0\) se denominan también corrientes neutras (NC). Y en este caso, como en el del fotón, el portador no transmite carga eléctrica.
Existen 8 tipos de gluones, que son electricamente neutros y de masa nula, pero sí tienen color. Intercambian el color de los quarks. Por ejemplo, decimos que un gluón cambia un quark rojo en azul y a cambio convierte un quark azul en rojo.
Como los gluones transmiten color, pueden interaccionar entre sí, intercambiandose entre ellos colores, esto es, interaccionan entre ellos.
De nuevo aunque no tenemos una expliación exacta en QCD, podemos entender el rango de interacción de los gluones limitado por las propias interacciones entre ellos.
1.7.5.2. Propiedades de las fuerzas#
Adelantamos ahora algunas propiedades de las fuerzas que se discutirán en los temas siguientes:
Las interacciones electromagnética y fuerte conservan:
el sabor,
la paridad.
Recordemos que paridad es la inversión de \({\bf x} \to - {\bf x}\), cambio de signo en las coordenadas espaciales; y la inversión de carga cambia todas las cargas de las partículas.
La interacción fuerte conserva además:
las cargas de color.
Esto es si los quarks iniciales son rojo y azul, entre los quarks finales hay rojo y azul.
En este sentido, las interacciones fuertes y electromagnéticas, son clásicas.
Por el contrario, la interacciones débiles, son peculiares y sorprendentes, poque violan
la paridad, (las cargadas de forma máxima).
Lo que es una caractística esencial de la interacción débil y una de las piezas angulares del Modelo Estándar.
la inversión conjunta de carga y paridad, CP.
Se viola de forma mínima y solo en corrientes cargadas en hadrones, (no sabemos hoy en día si también se viola en leptones). Aunque esta violación es muy relevante, sin embargo no tiene un caracter fundamental en la teoría, sino que aparece como una posibilidad al existir tres generaciones. Tampoco sabemos por qué se produce este nivel de violación CP, que matemáticamente se traduce en el valor de una fase compleja en una matriz unitaria (ver tema quark-hadrones).
Además, las corrientes cargadas cambian el sabor, pero las neutras lo conservan.
Por ejemplo, la interacción débil neutra entre un neutrino y un leptón cargado iniciales da lugar a una dispersión con el mismo neutrino y leptón cargado en el estado final.
Luego, la interacción más peculiar de todas es con diferencia la interacción débil cargada, la que media la desintegración \(\beta\) del neutrón.
1.7.6. El bosón de Higgs#
Ahora sabemos, o entendemos, que las partículas de forma primigenia no tienen masa, y ésta no es una propiedad intrínsica suya, sino que aparece por la interacción de cada tipo de fermión con el bosón de Higgs.
El bosón de Higgs es un scalar, su espín es \(0\), y obedece a la ecuación de Klein-Gordon.
Y como vemos juega un papel crucial en el SM:
dota de masas a las partículas.
dota de masas a los bosones véctoriales débiles \(W^\pm, Z^0\).
Aunque la masa aparece como consecuencia de la interacción con el Higgs, el modelo no predice sin embargo qué masa tienen los fermiones, ni qué masa tiene el Higgs. Lo que hace que las masas sean parámetros libres del modelo.
El Higgs además presenta interacciones entre otros higgs, con los bosones vectoriales débiles, y con los fermiones, lo que da lugar a la predicción de una física muy rica y compleja que es motivo de estudio actual en el LHC y lo será con seguridad en futuros aceleradores.
Estudiaremos las características del SM y del bosón de Higgs en el [Tema-SM]
1.8. Un repaso a la historia#
1.8.1. Hitos principales#
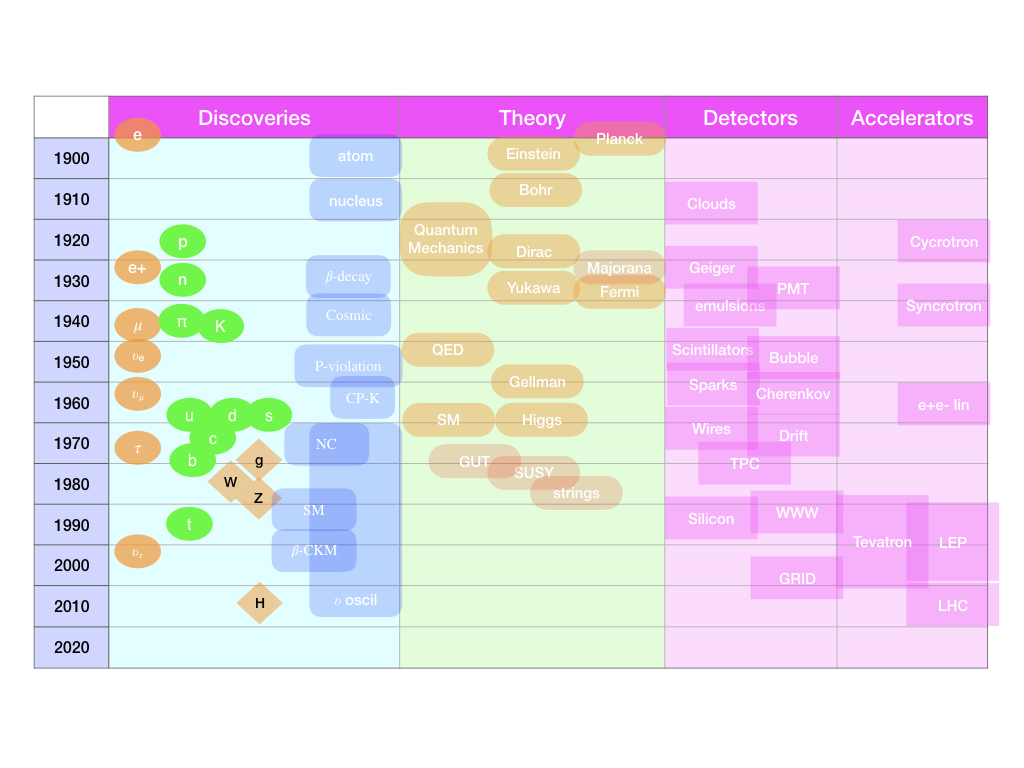
La siguiente tabla presenta algunos de los hitos principales en Física de Partículas, experimental, teórica y de detectores.
Hitos de la Historia de Física de Partículas |
A vuelo de pájaro:
Durante las primeras décadas del siglo XX se descubrieron los componentes del núcleo (los componentes de la materia ordinaria: protón, neutrón, electrón, neutrino).
En las décadas siguientes se descubrieron nuevos hadrones y leptones que se desintegraban (¿Quién ha ordenado ésto?, ¿por qué este bestiario de nuevas partículas?)
A principios de los 60” a partir del estudio de la estructura de los nucleones, se establece la existencia de los quarks (¡orden al fin!)
En las décadas de los 80-90 se confirma el Modelo Estándar (todo encaja, pero falta una pieza, el bosón de Higgs)
En el 2012 de descubre el bosón de Higgs (El modelo está completo, pero no es suficiente…)
1.8.2. Detectores, Experimentos, Teoría#
Enumeramos ahora como las tres ramas: detectores, experimental y teoría se complementan, y como han influido unas en otras a lo largo de la historia de la Física de Partículas
Nuevos detectores permiten nuevos descubrimientos:
Las emulsiones fotográficas permitieron la observación de partículas, \(\mu, \pi\)
Las centelleadores y los reactores nucleares el descubrimiento del neutrino \(\nu_e\).
Los detectores de silicio la determinación de partículas con vida corta \(\tau, B\)
Los experimentos revelan una Naturaleza inesperada:
La violación de Paridad y CP en corrientes débiles.
Tres familias de leptones y de quarks.
La matrix de mezcla, CKM, que rigue los corrientes cargadas entre los quarks.
Oscilaciones de neutrinos.
La construcción de la teoría guía a los descubrimientos:
Pauli postula la existencia del neutrino.
Gellman propone el modelo de quarks y la ordenación de “zoo” de hadrones.
La unificación electro-débil predice las corrientes neutras de neutrinos.
La rotura espontánea de simetría postula la existencia del bosón de Higgs.
Algunos de los avaces experimentales más relevantes son:
El descubrimento del positron (antimateria)
El descubrimiento de partículas inesperadas: \(\mu, ...\)
El descubrimiento del neutrino y sus propiedades.
La violación de Paridad y de CP en corrientes débiles
La existencia de los quarks y los gluones
La existencia de las corrientes neutras y la verificación del SM
La verificación de la matrix de mezclas CKM que rige la física del sabor de los hadrones.
El descubrimiento de oscilaciones de neutrinos
El descubrimiento del bosón de Higgs
Los avances teóricos más importantes:
La ecuación de Dirac y la existencia de la antimateria
El potencial de Yukawa
La teoría de Fermi de interacciones entre corrientes.
Los diagramas de Feynman (QED)
El modelo de quarks de Gellman and Zweig.
La unificación electro-débil, el Modelo Estándar (SM) de Glashow, Salam y Weinberg.
El mecanismo de Higgs y Englert.
1.8.3. Preguntas sin respuesta#
Aún quedan por resolver bastantes preguntas de las que no conocemos la respuesta:
¿Se conserva el número bariónico? ¿Se desintegra el protón?
¿Se conserva el número leptónico? ¿Es el neutrino su propia anti-partícula?
¿Son los quarks y leptones elementales? ¿Y el bosón de Higgs?
¿Por qué hay 3 generaciones?
¿Hay un patrón que explique las masas de los fermiones?
¿Por qué hay tanta disparidad de masas entre el neutrino y el resto de fermiones? ¿Se acopla el neutrino al bosón de Higgs?
¿Por qué el Universo está formado por materia y no por anti-materia? ¿Qué paso con la anti-materia del Universo?
¿Qué forma la materia oscura?
Si tenemos en cuenta que la materia del Universo que conocemos o decimos conocer supone un 5% del total, nos damos cuenta que queda aún mucho camino por recorrer…
1.8.4. Nomenclatura:#
nombres |
definición |
|---|---|
partícula |
corpúsculo que puede sentir la fuerzas electromagnética, débil o fuerte |
antipartícula |
partícula con las cargas y números cuánticos (excepto masa y spín) opuestos a la partícula |
fermión |
partícula de spin 1/2 |
leptón (ligero) |
fermión que no siente la fuerza fuerte |
quark |
fermión que siente la fuerza fuerte |
bosón |
particula de spín entero |
gauge boson |
bosones portadores de la fuerza \(W, Z, \gamma\) tienen spín 1 (vectoriales) |
hadrón (fuerte) |
partícula compuesta que siente la fuerza fuerte |
barión |
hadrón compuesto de tres quarks |
mesón (mediano) |
hadrón compuesto de quark y antiquark |
[Para esta sección ver MT1.1 y AB1.8, AB1.9]