Fundamentos de cinemática#

Jose A. Hernando

Departamento de Física de Partículas. Universidade de Santiago de Compostela

Noviembre 2023

import time
print(' Last version ', time.asctime() )

 Last version  Wed Jan 17 16:48:27 2024

# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2

# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

Cinemática de los observables#

Normalización en mecánica cuántica relativista#

normalización de la función de ondas#

En mecánica cuántica normalizamos la función de ondas, \(\psi\) en un cubo de lados \(L\), con volumen \(V = L^3\), a la unidad:

\[ \int_V \psi^* \psi \, \mathrm{d}^3x = 1 \]

Esto es, la partícula está contenida en \(V\).

La densidad de estados disponibles en ese volumen es:

\[ \frac{\mathrm{d}^3{\bf p}}{(2\pi)}, \]

que viene de expresar \(\frac{\mathrm{d}^3 {\bf p}}{h}\) en NU, recordando que en NU: \(h = 2\pi\).

El volumen sin embargo no es un invariante Lorentz.

Un cubo de lado \(L\) en un sistema con un factor de Lorentz \(\gamma\) es:

\[ V ' = \gamma L^3 = \gamma V \]

Si en ese cubo estaba contenida la partícula con energía \(E_0 \), en el sistema de referencia con factor \(\gamma\), su energía es:

\[ E' = \gamma E_0 \]

Vemos que \(V, E\) se tranforman Lorentz de igual forma, via un factor \(\gamma\).

En mecánica cuántica relativista, normalizamos la función de ondas, \(\Psi\), en un volumen \(V\) a \(2E\):

\[ \int_V \Psi^* \Psi \, \mathrm{d}^3 x = 2E, \]

El factor \(2\) es por conveniencia.

Esta normalización sí es relativista porque el volumen, \(V\), y la energía, \(E\), cambian con el mismo factor al cambiar el sistema de referencia.

Elemento de matriz relativista#

Como consecuencia de la normalización relativista de la función de ondas \(\Psi\), el elemento de matriz relativista \(|M_{fi}| = \langle \Psi_f| H_{int}| \Psi_i \rangle\) se relaciona con el no-relativista \(T_{fi} = \langle \psi_f | H_{int}| \psi_i \rangle\) por un factor que proviene de la normalización.

\[ M_{fi} = \langle \Psi_f | H_{int}| \Psi_i \rangle = \left(\prod_i \sqrt{2E_i} \right) \langle \psi_f | H_{int}| \psi_i \rangle = \left(\prod_i \sqrt{2E_i} \right) T_{fi} \]

donde el índice \(i\) corre en las \(n\) partículas iniciales y finales.

Las expresiones de la amplitud de transición o de la sección eficaz en el tratamiento relativista incorporan por lo tanto el siguiente factor:

\[ \frac{1}{\prod_i (2E_i)}, \]

debido a la normalización relativista.

Amplitud de desintegración#

La expresión no-relativista de la amplitud de desintegración de una partícula de \(E_a\) a \(m\) partículas finales es:

\[ \Gamma = (2\pi)^4 \int |T_{fi}|^2 \delta^4 \left(\sum_k p_k - p_a \right) \, \prod_i \frac{\mathrm{d}^3{\bf p}_i}{(2\pi)^3} \]

donde \(p_a\) es el cuadrimomento de la partícula inicial y \(p_i\) los de las finales, \(i = 1, \dots, m\). Recordar que las deltas de Dirac imponen la conservación de energía y momento entre la partícula inicial y las finales.

Y la relativista:

\[ \Gamma = \frac{(2\pi)^4}{2 E_a} \int |M_{fi}|^2 \delta^4 \left(\sum_k p_k - p_a \right) \, \prod_i \frac{\mathrm{d}^3{\bf p}_i}{(2\pi)^3 (2E_i)} \]

Sección eficaz de la interacción de dos partículas \( a + b\)#

La expresión no relativista para la sección eficaz de \(a+b\) para producir \(m\) partículas es:

\[ \sigma = \frac{(2\pi)^4}{|v_a + v_b|} \int |T_{fi}|^2 \delta^4 \left(\sum_k p_k - p_a - p_b \right) \, \prod_i \frac{\mathrm{d}^3{\bf p}_i}{(2\pi)^3}, \]

donde \(v_a, v_b\) son el módulo de las velocidades, considerando que las partículas colisionan en una misma dirección y tienen sentidos opuestos. Las deltas de Dirac imponen la condición de conservación de la energía y momento entre los estados inicial y final.

La expresión relativista es:

\[ \sigma = \frac{(2\pi)^4}{(2 E_a) (2 E_b) (\beta_a + \beta_b)} \int |M_{fi}|^2 \delta^4 \left(\sum_k p_k - p_a -p_b\right) \, \prod_i \frac{\mathrm{d}^3{\bf p}_i}{(2\pi)^3 (2E_i)} \]

En la versión relativista, cada uno de los factores de la sección eficaz es invariante Lorentz:

  • el elemento de matriz al cuadrado: \(|M_{fi}|^2 = | \langle \Psi_f| H_{int} | \Psi i\rangle |^2\)

  • la densidad de estados: \(\frac{\mathrm{d}^3 {\bf p}}{(2\pi)^3 (2E)}\)

  • el término asociado al flujo: \(4 E_a E_b (\beta_a + \beta_b)\)

Notar que a partir de la propiedad de la función delta de Dirac, \(\int \delta(E^2-{\bf p}^2 - m^2) \, \mathrm{d}E = \frac{1}{2E}\), podemos reescribir:

\[ \frac{\mathrm{d}^3{\bf p}}{(2\pi)^3 (2E)} = \int \delta(p^2-m^2) \frac{\mathrm{d}^4p}{(2\pi)^3} \]

Cuestión: Demostrar que \(4 E_a E_b (\beta_a + \beta_b) = 16 \sqrt{(p_a \cdot p_b)^2 - m^2_a m^2_b}\)

Anchura de desintegración a dos partículas#

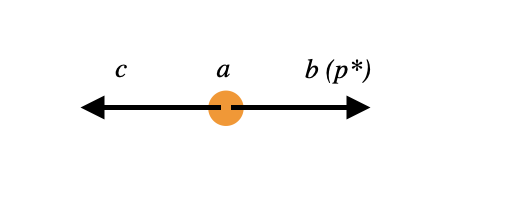
Consideremos la desintegración de una partícula \(a\) en dos \(b, d\), con masas \(m_a, m_b, m_c\).

../_images/intro_drawing_decay2.png

Esquema de desintegración de la partícula \(a\) a dos \(b, c\) en el CM

El sistema más conveniente para tratar el proceso es el CM, donde la partícula \(a\) está en reposo, y tiene \(E = m_a\).

Las partículas \(b, c\) salen con momentos opuestos \({\bf p}^* = {\bf p}_b = - {\bf p}_c\).

El módulo del momento de las partículas salientes, \(p^*\) es (ver sección de los invariantes de Mandelstam):

\[ p^*= \frac{1}{2m_a} \sqrt{[m^2_a - (m_b+m_c)^2] \, [m^2_a - (m_b - m_c)^2] } \]

La anchura de desintegración, \(\Gamma\), es la razón de transición de la regla de oro de Fermi.

Integramos usando \(\delta({\bf p}_b + {\bf p}_c)\) en \(\mathrm{d}^3p_{c}\) directamente.

\[ \Gamma = \frac{1}{(2 E) (2\pi)^2} \int |M_{fi}|^2 \delta \left(E - E_b - E_c \right) \frac{p^2_b }{4 E_b E_c}\, \mathrm{d}p_b \mathrm{d}\Omega^*, \]

donde \(E_b = \sqrt{m^2_b + p^2_b}, \; E_c = \sqrt{m^2_c + p^2_b}\) y \(\mathrm{d}\Omega^*\) el diferencial de ángulo sólido.

Si aplicamos la siguiente propiedad de la delta de Dirac: \(\int \delta(f(p))\, \mathrm{d} p = \left|\frac{\mathrm{d}f(p)}{\mathrm{d}p} \right|_{p'}^{-1}\), donde \(p'\) cumple \(f(p') = 0\)

con \(f(p_b) = E - \sqrt{m^2_b + p^2_b}- \sqrt{m^2_c + p^2_b}\) respecto \(p = p_b\), y \(p' = p^*\):

\[ \frac{\mathrm{d}f(p_b)}{\mathrm{d}p_b} = \frac{p_b}{\sqrt{m^2_b + p^2_b}} + \frac{p_b}{\sqrt{m^2_c + p^2_c}} = p_b \frac{E_c + E_d}{E_c E_d} = p_b \frac{E}{E_c E_d} \]

La anchura de desintegración queda:

\[ \Gamma = \frac{1}{8 \pi^2 E} \frac{(p^*)^2}{4 E_b E_c} \frac{E_b E_c}{p^* E} \int |M_{fi}|^2 \, \mathrm{d}\Omega^* = \frac{1}{8\pi^3}\frac{p^*}{4 E^2} \int |M_{fi}|^2 \, \mathrm{d}\Omega^* \]

La anchura de desintegracion, en este caso, solo depende de \(p^*\), si colocamos \(E = E_a = m_a\) en el CM:

\[ \Gamma = \frac{p^*}{32 \pi^2 m^2_a} \int_{\Omega} |M_{fi}|^2 \mathrm{d}\Omega^* \]

Sección eficaz de una interacción de dos cuerpos#

Sea la interacción entres dos partículas \(a, b\) que da lugar a \(m\) particulas finales.

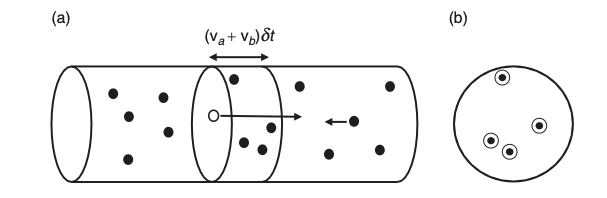
Sea un flujo de partículas \(a\), con densidad de \(N_a\) partículas en un volumen \(V\), que se mueve contra \(N_b\) partículas blanco en un volumen \(V\) que a su vez se mueven en sentido opuesto con \(v_b\).

Asignamos una sección eficaz \(\sigma\) de interacción a la partículas blanco \(b\). La frecuencia de interacciónes corresponderá al número de partículas \(a\) que atraviesa un cilindro de base \(\sigma\) y altura \(v_a + v_b\) para cada partícula \(b\).

../_images/fun_drawing_xsection.png

(a) una partícula \(a\) recorre en \(\mathrm{d}t\) un cilindro de longitud \(v_a+v_b\) [MT3.4]

(b) visión transversal del cilindro, las partículas \(b\) en el mismo con el disco de la sección eficaz

Esto es, en número de interacciones en un volumen \(V\) y un tiempo \(\mathrm{d}t\) es:

\[ \mathrm{d}N = (v_a + v_b) \sigma \, n_a N_b \, \mathrm{d}t \]

El factor \((v_a + v_b) n_a\) es el flujo de partículas \(a\), \(\phi_a\), con velocidad \(v_a\) que atraviesan una superficie perpendicular a su velocidad, cuando ésta se mueve contra ellas con velocidad \(v_b\).

Luego, la frecuencia de interacciones, \(R\), en un volumen, V, donde hay \(N_b\), partículas blanco, al que llega un flujo \(\phi_a\) de partículas \(a\) es:

\[ R = \phi_a \, \sigma \, N_b \]

En mecánica cuántica se adopta la normalización de una partícula en una unidad de volumen, \(V = 1, n_a = 1, n_b = 1\), en ese caso:

\[ R = (v_a + v_b) \, \sigma, \;\;\; \sigma = \frac{R}{(v_a+v_b)} \]

En la formulación relativista, tenemos que introducir el factor de normalización \(\frac{1}{(2E)}\) para cada partícula.

\[ \sigma = \frac{(2\pi)^4}{(2 E_a) (2 E_b) (\beta_a + \beta_b)} \int |M_{fi}|^2 \delta^4 \left(\sum_k p_k - p_a -p_b\right) \, \prod_i \frac{\mathrm{d}^3{\bf p}_i}{(2\pi)^3 (2E_i)} \]

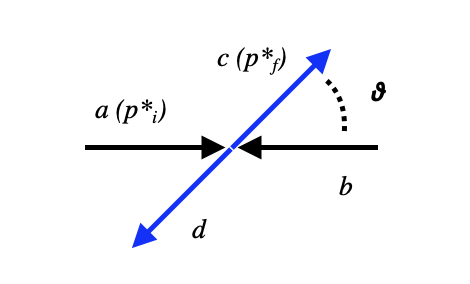
Sea la interacción entre dos partículas, \(a, b\) , incidentes que da lugar a dos partículas finales \(c, d\).

../_images/intro_drawing_int2.png

Esquema de interacción de las partículs \(a, b\) a \(c, d\) en el CM

El sistema más conviente para calcula la sección eficaz es el CM. En este sistema, se conservan los momentos:

\[ {\bf p}^*_i = {\bf p}_a = - {\bf p}_b, \;\; {\bf p}^*_f = {\bf p}_c = - {\bf p}_d \]

Notar que las partículas están en un plano, y el único parámetro libre es el ángulo, \(\theta^*\) entre \({\bf p}^*_f\) y \({\bf p}^*_i\), y este último define el eje.

La sección eficaz se obtiene a partir de la expresión general donde \(E = E_a + E_b\), \(p_b = p_a = p^*_i\) y \(p_d = p_c = p^*_f\).

El término del espacio fásico se calcula igual que en el apartado de la amplitud de desintegración a dos cuerpos, solo que ahora \(E = E_a + E_b\):

\[ \frac{1}{(2\pi)^2}\frac{p^*_f}{4 E} \int |M_{fi}|^2 \, \mathrm{d}\Omega^* \]

El término asociado al flujo:

\[ 4 E_a E_b (\beta_b + \beta_a) = 4 E_a E_b \left(\frac{p_a}{E_a} + \frac{p_b}{E_b}\right) = 8 E p^*_i \]

La sección queda:

\[ \sigma = \frac{1}{64 \pi^2 E^2} \frac{p^*_f}{p^*_i} \int_\Omega |M_{fi}|^2 \, \mathrm{d}\Omega^* \]

Si sustituimos \(E^2 = s\) donde \(s = \left[(E_a, {\bf p}_a) + (E_b, {\bf p}_b)\right]^2 = [(E_a + E_b, {\bf 0})]^2\), es el cuadrimomento transferido al cuadrado.

\[ \sigma = \frac{1}{64 \pi^2 s} \frac{p^*_f}{p^*_i} \int_\Omega |M_{fi}|^2 \, \mathrm{d}\Omega \]

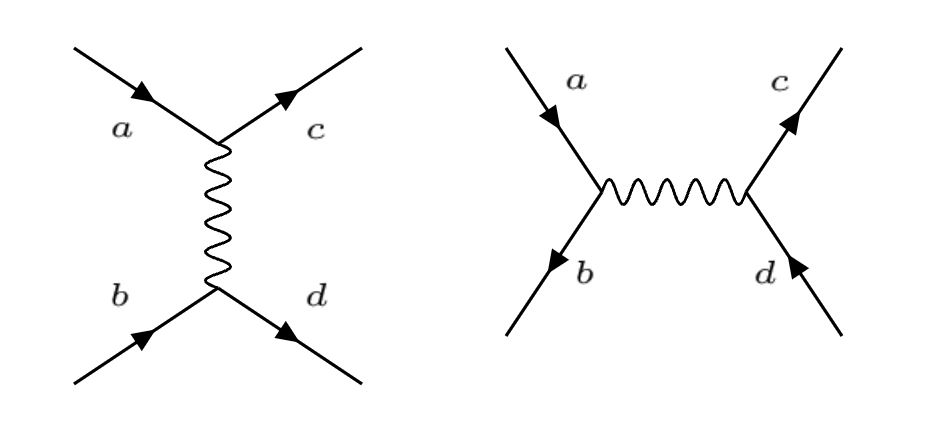
Invariantes de Mandelstam#

../_images/feynman_stchannels.png

Diagramas asociados a los invariantes de Mandelstam (izda) dispersión (derecha) aniquilación

Los cuadrimomentos transferidos, \(q^2\), entre las corrientes, de los diagramas de la figura, se denota con:

\[ t = (p_c - p_a)^2 = (p_d - p_b)^2, \;\;\; s = (p_a +p_b)^2 = (p_c + p_d)^2, \]

donde \(p_\alpha\), \(\alpha = a, b, c, d\) son los cuadrimomentos de las partículas,

y se denominan invariantes de Mandelstam y que corresponden a los canales \(t\) de dispersión y \(s\) de aniquilación respectivamente.

Cinemática con el invariante \(s\)#

La cantidad \(\sqrt{s}\) es la energía en el centro de masas, (CM), de una aniquilación

\[ s = (p_a + p_b) = (E^*_a + E^*_b) - ({\bf p}^*_a +{\bf p}^*_b) = (E^*_a + E^*_b)^2, \]

dado que \({\bf p}^*_i = {\bf p}^*_a = -{\bf p}^*_b\) (ver figura de la dispersión de dos cuerpos arriba).

En la literatura se denota \(\sqrt{s}\) para indicar la energía en el centro de masas.

Podemos calcular \(E^*_a, E^*_b\) a partir de \(s\) y las masas \(m_a, m_b\).

Si calculamos, \(E^{*2}_a\) teniendo en cuenta que \(E^*_a = (\sqrt{s} - E^*_b)\), y \(p^*_a = p^*_b = p^*_i\), obtenemos:

\[\begin{split} E^{*2}_a = m^2_a + p_i^{*2} = E^{*2}_b - 2 \sqrt{s}E^*_b + s = m^2_b + p_i^{*2} - 2 \sqrt{s}E^*_b + s \\ m^2_a = m^2_b + s - 2 \sqrt{s} E^*_b \end{split}\]

y como el tratamiento para \(a\) es idéntico al de \(b\), obtenemos:

\[ E^*_a = \frac{s + m^2_a - m^2_b}{2 \sqrt{s}}, \;\; E^*_b = \frac{s + m^2_b - m^2_a}{2 \sqrt{s}}. \]

El momento será:

\[\begin{split} p^{*}_i = \sqrt{E^{*2}_a - m^2_a} = p^* = \sqrt{E^{*2}_b - m^2_b}, 2 p^{2*} = E^{*2}_a + E^{*2}_b - m^2_a - m^2_b \\ \end{split}\]

por lo tanto

\[\begin{split} p^{2*}_i = \frac{E^{*2}_a + E^{*2}_b - m^2_a - m^2_b}{2} = \\ \frac{\left[s + (m^2_a - m^2_b) \right]^2 + \left[s - (m^2_a - m^2_b)\right]^2 - 4 s (m^2_a + m^2_b)}{8 s} = \\ \frac{s^2 + (m^2_a - m^2_b)^2 - 2 s (m^2_a + m^2_b)}{4s} \end{split}\]

como:

\[\begin{split} m^2_a - m^2_b = (m_a + m_b) (m_a - m_b), \\ 2(m^2_a + m^2_b) = (m_a+m_b)^2 + (m_a-m_b)^2 \end{split}\]

tenemos:

\[\begin{split} p^{*2}_i = \frac{s^2 + (m_a+m_b)^2(m_a-m_b)^2 - s \left[ (m_a+m_b)^2 + (m_a - m_b)^2 \right] }{4s} = \\ = \frac{\left[s- (m_a+m_b)^2\right] \, \left[s - (m_a-m_b)^2\right]}{4s} \end{split}\]

por lo que el momento inicial es:

\[ p^*_i = \frac{\sqrt{\left[s- (m_a+m_b)^2\right] \, \left[s - (m_a-m_b)^2\right]}}{2\sqrt{s}} \]

Como la situación es idéntica para las partícula finales tenemos:

\[\begin{split} E^*_c = \frac{s + m^2_c - m^2_d}{2 \sqrt{s}}, \;\; E^*_d = \frac{s + m^2_d - m^2_c}{2 \sqrt{s}} \\ p^*_f = \frac{\sqrt{\left[s- (m_c+m_d)^2\right] \, \left[s - (m_c-m_d)^2\right]}}{2 \sqrt{s}} \end{split}\]

En el caso de la desintegración a dos cuerpos, \(a \to c + d\), la energía en el CM es \( \sqrt{s} = m_a\).

Los momentos y energía finales son en ese caso:

\[\begin{split} E^*_c = \frac{m^2_a + m^2_c - m^2_d}{2 m_a}, \;\; E^*_d = \frac{m^2_a + m^2_d - m^2_c}{2 m_a} \\ p^*_f = \frac{1}{2m_a}\sqrt{\left[m^2_a- (m_c+m_d)^2\right] \, \left[m^2_a - (m_c-m_d)^2\right]} \end{split}\]

Cinemática con el invariante \(t\)#

El invariante t, \(t = (p_c - p_a)^2 = (p_d - p_b)^2\), es:

\[\begin{split} t = (p_c - p_a)^2 = p^2_c + p^2_a - 2 p_c \cdot p_a = m^2_a + m^2_c + 2 |{\bf p}_a| |{\bf p}_c| \cos \theta_{ab} - 2 E_a E_c \\ t = (p_d - p_b)^2 = p^2_d + p^2_b - 2 p_d \cdot p_b = m^2_b + m^2_d + 2 |{\bf p}_b| |{\bf p}_d| \cos \theta_{bd} - 2 E_b E_d \end{split}\]

donde \(\theta_{ac}, \theta_{bd}\) son los ángulos entre los momentos de \(ac\) y \(bd\) respectivamente.

En el sistema de laboratorio \(p_b = (m_b, {\bf 0})\), tenemos :

\[ t = m^2_b + m^2_d - 2m_b E_d, \;\; E_d = \frac{m^2_b + m^2_d - t}{2m_b} \]

En el sistema CM (ver figura de la interacción a dos cuerpos), \(|{\bf p}_a| = p^*_i, \; |{\bf p}_c| = p^*_f\) y \(\theta_{ac} = \theta^*\)

\[\begin{split} t = m^2_a + m^2_c + 2 p^*_i p^*_f \cos \theta^* - 2E_a E_c, \\ \cos \theta^* = \frac{t - m^2_a - m^2_b + 2E^*_aE^*_c}{2 p^*_i p^*_f} \end{split}\]

Bibliografía#

  • [AB1.3, AB1.6] Alessandro Bettini, «Introduction to Elementary Particle Physcs», Cambridge U. press.

  • [MT4, MT6.4] Mark Tomson, «Modern Particle Physics», Cambridge U. press.