Boletín de problemas I
12. Boletín de problemas I#
Jose A. Hernando
Departamento de Física de Partículas. Universidade de Santiago de Compostela
Octubre 2024
import time
print(' Last version ', time.asctime() )
Last version Wed Dec 18 17:08:09 2024
# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2
# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.constants as units
print('hbar = {:4e} J/s'.format(units.hbar))
print('c = {:4e} m/s'.format(units.c))
GeV_to_Julio = units.giga * units.eV
print('GeV = {:4e} J '.format(GeV_to_Julio))
hbarc = units.hbar * units.c / (GeV_to_Julio * units.femto) # GeV fm
print('hbar c = {:4e} GeV fm'.format(hbarc))
hbar = 1.054572e-34 J/s
c = 2.997925e+08 m/s
GeV = 1.602177e-10 J
hbar c = 1.973270e-01 GeV fm
me = (units.m_e * units.c**2)/(GeV_to_Julio) # GeV
mp = (units.m_p * units.c**2)/(GeV_to_Julio) # GeV
print('electron mass {:4.3f} MeV'.format(me *1e3))
print('proton mass {:4.3f} GeV'.format(mp))
electron mass 0.511 MeV
proton mass 0.938 GeV
energy = lambda m, p : np.sqrt(m**2 + p**2)
momentum = lambda m, E : np.sqrt(E**2 - m**2)
gamma_lorentz = lambda m, E : m/E
beta_lorentz = lambda p, E : p/E
kinetic_energy = lambda m, E : E - m
mass_invariant = lambda p: np.sqrt(p[0]**2 - momentum_module(p)**2)
momentum_module = lambda p: np.sqrt( p[1:].dot(p[1:]) )
phi_angle = lambda p: np.arctan2(p[2], p[1])
def theta_angle(p):
rho = np.sqrt(p[1]**2 +p[2]**2)
theta = np.arctan2(rho, p[3])
phi = np.arctan2(p[2], p[1])
return theta if phi < np.pi/2 else -theta
def lorentz_matrix(beta):
gamma = 1/np.sqrt(1 - beta**2)
lorentz = np.zeros(16).reshape(4, 4)
lorentz[0, 0] = gamma; lorentz[0, 3] = gamma * beta
lorentz[1, 1] = 1 ; lorentz[2, 2] = 1
lorentz[3, 3] = gamma; lorentz[3, 0] = gamma*beta
return lorentz
def lorentz_transform(beta, p):
lorentz = lorentz_matrix(beta)
return lorentz.dot(p.transpose())
def p_write(p, name):
print('{:s}: p = [{:4.3f}, {:4.3f}, {:4.3f}, {:4.3f}]'.format(name, *p))
print('{:s}: |p| = {:4.3f}, mass = {:4.3f}'.format(name, momentum_module(p), mass_invariant(p)))
return
energy_cm_2body_s = lambda s , mb, mc: (s + mb**2 - mc**2)/ (2 * np.sqrt(s))
energy_cm_2body = lambda ma, mb, mc: energy_cm_2body_s(ma**2, mb, mc)
momentum_cm_2body_s = lambda s , mb, mc: np.sqrt( (s - (mb + mc)**2) * ( s - (mb - mc)**2) )/ (2 * np.sqrt(s))
momentum_cm_2body = lambda ma, mb, mc: momentum_cm_2body_s(ma**2, mb, mc)
problema 1
Da en unidades naturales los valores:
a) fs y fm en potencias de GeVs.
b) m, s en potencias de eV.
c) barn en función de GeV.
solución:
a) sabemos \(\hbar c = 197 \) MeV fm = 1, luego fm \(= \frac{1}{197}\) MeV\(^{-1}\)
c) sabemos \(c = 2.9998 \, 10^8\) m/s = 1,luego s \(= 2.9998 \, 10^8\) m, luego fs = c fm
d) sabemos 1 barn = \(10^{-28}\) m\(^2\), cambiamos m a 1/GeV
print('hbarc = {:e} GeV fm'.format(hbarc))
fm_un = 1/hbarc #1/GeV
print('fm = {:e} 1/GeV '.format(fm_un))
ps_un = units.femto * (units.c / (units.femto)) * fm_un
print('fs = {:e} 1/GeV '.format(ps_un))
m_un = fm_un/(units.femto) # 1/GeV
print('m = {:e} 1/eV, eV = {:e} 1/m '.format(m_un/units.giga, units.giga/m_un))
#s_un = fs_un / (units.femto)
#print('s = {:e} 1/eV, eV = {:e} 1/s '.format(s_un/units.giga, units.giga/s_un))
m_un = fm_un / (units.femto)
barn = 1e-28 * (m_un)**2
print('barn = {:e} 1/GeV2 '.format(barn))
hbarc = 1.973270e-01 GeV fm
fm = 5.067731e+00 1/GeV
fs = 1.519267e+09 1/GeV
m = 5.067731e+06 1/eV, eV = 1.973270e-07 1/m
barn = 2.568189e+03 1/GeV2
problema 2
Compara energía de un Boeing 747, cuya masa es 400 toneladas, a su velocidad crucero de 850 km/h, con la aniquilación de un mosquito por un antimosquito, siendo la masa del mosquito 1 mg.
mb = 400e3 # kg
mm = 1.0e-6 # kg
v = 850e3/(60*60) # m/s
boeing_ene = 0.5 * mb * v**2
mosquito_ene = 2 * mm * units.c**2
print('energy boeing/mosquito {:4.3f}'.format(boeing_ene/mosquito_ene))
print('boeing {:e} J, mosquito {:e} J'.format(boeing_ene, mosquito_ene))
print('boeing {:e} GeV, mosquito {:e} GeV'.format(boeing_ene/GeV_to_Julio, mosquito_ene/GeV_to_Julio))
energy boeing/mosquito 0.062
boeing 1.114969e+10 J, mosquito 1.797510e+11 J
boeing 6.959090e+19 GeV, mosquito 1.121918e+21 GeV
problema 3
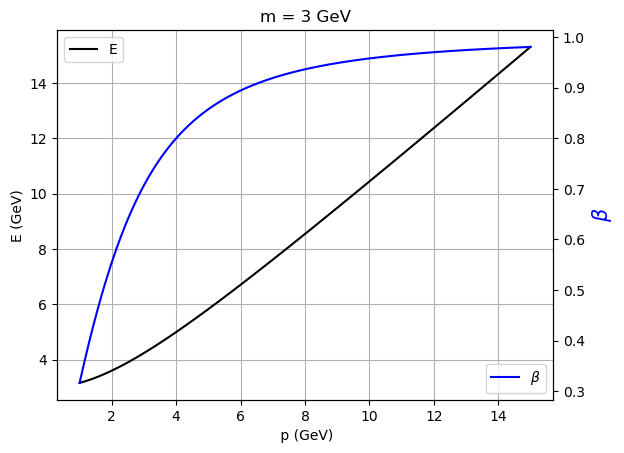
¿Cuál es la energía y velocidad de una partícula de 3 GeV de masa con un momento de 4 GeV en la dirección \(z\)?
m, p = 3, 4 # GeV
E = energy(m, p)
b = beta_lorentz(p, E)
print('energy (MeV) {:3.3f}'.format(E))
print('velocity (beta) {:3.2f} velocity (m/s) {:2e}'.format(b, b * units.c))
ps = np.linspace(1, 15, 100)
plt.plot(ps, energy(m, ps), c = 'black', label = 'E')
plt.xlabel(' p (GeV)'); plt.ylabel('E (GeV)'); plt.title('m = 3 GeV')
plt.grid(); plt.legend();
ax = plt.gca().twinx()
plt.plot(ps, beta_lorentz(ps, energy(m, ps)), c = 'blue', label = r'$\beta$')
plt.ylabel(r'$\beta$', c = 'blue', fontsize = 15); plt.legend(loc=4);
energy (MeV) 5.000
velocity (beta) 0.80 velocity (m/s) 2.398340e+08
problema 4
Sea una partícula \(a\) con masa \(m_a\) que se desintegra a otras dos \(a \to b+c\), con masas \(m_b, m_c\). Da las expresiones de la energía y momento de \(b, c\) en el CM. Demostrar que el momento de las partículas hijas en el CM es:
solución
Ver [Extensión cinemática], sección del invariante s]
ejercicio 5 (antiguo)
Sean \(\Lambda \to p + \pi^-\) y \(\Xi^- \to \Lambda + \pi^-\). ¿Cuál es la carga de \(\Lambda\)? Indica si son bariones o mesones \(\Lambda\) y \(\Xi^-\). Busca sus masas en PDG, sus vidad medias y su fracción de desintegración. ¿Qué tipo de desintegración es, débil o fuerte? Da el momento y energía en CM de la desintegración
solución
Del PDG
\(m(\Lambda) = 1115.683 \pm 0.006\) MeV, \(\mathcal{Br}(\Lambda \to p + \pi^-) = 63.9 \pm 0.5\) %, \(\tau = (2.632 \pm 0.02) \, 10^{-10}\) s
Del PDG
\(m(\Xi^-) = 1321.71 \pm 0.07\) MeV, \(\mathcal{Br}(\Xi^- \to \Lambda + \pi^-) = 99.9\) %, \(\tau = (1.639 \pm 0.015) \, 10^{-10}\) s
Los dos son bariones, \(\Lambda\) tiene carga 0, y por el valor de la vida media se desintegran débilmente.
energy_cm_2body_s = lambda s , mb, mc: (s + mb**2 - mc**2)/ (2 * np.sqrt(s))
energy_cm_2body = lambda ma, mb, mc: energy_cm_2body_s(ma**2, mb, mc)
momentum_cm_2body_s = lambda s , mb, mc: np.sqrt( (s - (mb + mc)**2) * ( s - (mb - mc)**2) )/ (2 * np.sqrt(s))
momentum_cm_2body = lambda ma, mb, mc: momentum_cm_2body_s(ma**2, mb, mc)
mlambda = 1115.68 # MeV
mp = 938.27 # MeV
mpi = 139.6 # MeV
ep = energy_cm_2body (mlambda, mp , mpi)
epi = energy_cm_2body (mlambda, mpi, mp)
pp = momentum_cm_2body(mlambda, mp , mpi)
print('E p {:4.3f} MeV' .format(ep))
print('E pi {:4.3f} MeV'.format(epi))
print('p {:4.3f} MeV'.format(pp))
E p 943.642 MeV
E pi 172.038 MeV
p 100.544 MeV
mxi = 1321.71 # MeV
ep = energy_cm_2body (mxi, mlambda, mpi)
epi = energy_cm_2body (mxi, mpi , mlambda)
pp = momentum_cm_2body(mxi, mlambda, mpi)
print('E p {:4.3f} MeV' .format(ep))
print('E pi {:4.3f} MeV'.format(epi))
print('p {:4.3f} MeV'.format(pp))
E p 1124.366 MeV
E pi 197.344 MeV
p 139.487 MeV
problema 5
Considera la desintegración \(K^- \to \mu + \bar{\nu}_\mu\). Calcula la energía y momento en el CM del \(\mu, \bar{\nu}_\mu\) y el máximo momento del \(\mu\) si el \(K^-\) tienen un momento de 5 GeV.
La energía y momento del leptón son: $\( E_l = \frac{m^2_K + m^2_l}{2 m_K}, \; \; p_l = \frac{m^2_K - m^2_l}{2 m_K}, \;\; \)$
El momento máximo corresponderá al momento del \(\mu\) en la dirección y sentido del \(K\) incidente, que recibirá un boost de \(\gamma = E_K/m_K, \; \beta = p_K/E_K\). Asi:
ene_cm = lambda ml, mhad = mpi : (mhad**2 + ml**2)/(2*mhad)
p_cm = lambda ml, mhad = mpi : (mhad**2 - ml**2)/(2*mhad)
mkaon = 493.67 # MeV
mmu = 105.66 # MeV
e_mu, p_mu = ene_cm(mmu, mkaon), p_cm(mmu, mkaon)
e_nu, p_nu = p_mu, p_mu
print(' energy mu = {:5.3f} MeV'.format(e_mu))
print(' momento mu = {:5.3f} MeV '.format(p_mu))
e_kaon = 5000 # MeV
p_kaon = momentum(mkaon, e_kaon)
gamma_kaon, beta_kaon = e_kaon/mkaon, p_kaon/e_kaon
p_max_mu = gamma_kaon * beta_kaon * e_mu + gamma_kaon * p_mu
print(' momentum mu maximo en lab = {:5.3f} MeV '.format(p_max_mu))
p_min_nu = gamma_kaon * beta_kaon * e_nu - gamma_kaon * p_nu
print(' momentum nu minimo en lab = {:5.3f} MeV '.format(p_min_nu))
energy mu = 258.142 MeV
momento mu = 235.528 MeV
momentum mu maximo en lab = 4987.225 MeV
momentum nu minimo en lab = -11.656 MeV
mpi = 139.6 # MeV
me = 0.511 # MeV
emu = energy_cm_2body (mpi, me, 0)
enu = energy_cm_2body (mpi, 0 , me)
pcm = momentum_cm_2body(mpi, me, 0)
print('E elec {:4.3f} MeV'.format(emu))
print('E nu {:4.3f} MeV'.format(enu))
print('p {:4.3f} MeV'.format(pcm))
E elec 69.801 MeV
E nu 69.799 MeV
p 69.799 MeV
ejercicio 6
La partícula \(\Lambda\), se desintegra \(\Lambda \to p + \pi^-\). Si \(p_\Lambda = 2\) GeV y el \(p\) sale con \(\theta^* = 30^o\) en el CM respecto la dirección de \(\Lambda\), calcular:
a) la energía de \(\Lambda, \pi^-\) en el CM.
b) el factor de Lorentz \(\gamma\) y \(\beta\) entre el sistema laboratorio y el CM.
c) ángulo y momento del \(\pi, p\) en el sistema laboratorio.
mlambda = 1115.68 # MeV
mp = 938.27 # MeV
mpi = 139.57 # MeV
ep = energy_cm_2body (mlambda, mp , mpi)
epi = energy_cm_2body (mlambda, mpi, mp)
pp = momentum_cm_2body(mlambda, mp , mpi)
print('E p = {:4.3f} MeV'.format(ep))
print('E pi = {:4.3f} MeV'.format(epi))
print('p = {:4.3f} MeV'.format(pp))
E p = 943.645 MeV
E pi = 172.035 MeV
p = 100.579 MeV
plambda = 2000
elambda = energy(mlambda, plambda)
print('lambda energy {:4.3f} MeV'.format(elambda))
gamma = gamma_lorentz(elambda, mlambda)
beta = beta_lorentz (plambda, elambda)
print('beta = {:4.3f}, gamma {:4.3f} '.format(beta, gamma))
lambda energy 2290.140 MeV
beta = 0.873, gamma 2.053
Se cumple que: $\( p_x = p \sin \theta = p^* \sin \theta^*,\\ p_z = p \cos \theta = \gamma(\beta E + p^* \cos \theta^*) \)\( donde \)p, \theta$ es el momento y el ángulo en el lab.
Luego:
theta_cm = (30./180.) * np.pi
pp_cm = np.array((ep , pp *np.sin(theta_cm), 0, pp * np.cos (theta_cm)))
ppi_cm = np.array((epi, -pp *np.sin(theta_cm), 0, -pp * np.cos (theta_cm)))
pla_cm = ppi_cm + pp_cm
p_write(ppi_cm, 'pi')
p_write(pp_cm , 'p')
p_write(pla_cm, 'lambda')
print('pi : theta = {:4.1f} (o) '.format(theta_angle(ppi_cm) * (180/np.pi)))
pi: p = [172.035, -50.289, 0.000, -87.104]
pi: |p| = 100.579, mass = 139.570
p: p = [943.645, 50.289, 0.000, 87.104]
p: |p| = 100.579, mass = 938.270
lambda: p = [1115.680, 0.000, 0.000, 0.000]
lambda: |p| = 0.000, mass = 1115.680
pi : theta = -150.0 (o)
lorentz = lorentz_matrix(beta)
pp_lab = lorentz.dot( pp_cm .transpose() )
ppi_lab = lorentz.dot( ppi_cm.transpose() )
pla_lab = ppi_lab + pp_lab
p_write(ppi_lab, 'pi')
p_write(pp_lab , 'p')
p_write(pla_lab, 'lambda')
print('p : theta = {:4.1f} (o) '.format(theta_angle(pp_lab ) * (180/np.pi)))
print('pi : theta = {:4.1f} (o) '.format(theta_angle(ppi_lab) * (180/np.pi)))
pi: p = [196.988, -50.289, 0.000, 129.597]
pi: |p| = 139.013, mass = 139.570
p: p = [2093.152, 50.289, 0.000, 1870.403]
p: |p| = 1871.079, mass = 938.270
lambda: p = [2290.140, 0.000, 0.000, 2000.000]
lambda: |p| = 2000.000, mass = 1115.680
p : theta = 1.5 (o)
pi : theta = -21.2 (o)
ejercicio 7
Encontrar el ángulo mínimo de apertura entre los fotones de la desintegración \(\pi^0 \to \gamma \gamma\) si la energía del pión es 10 GeV.
solución
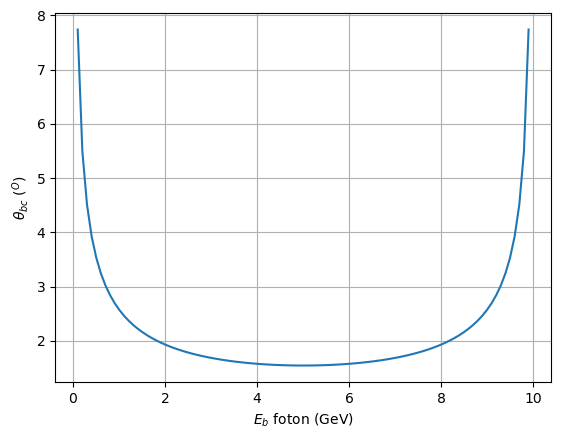
Sea \(a \to b + c\), \(p_a = p_b + p_c\), en el sistema laboratorio $\( s = (E_b + E_c, {\bf p}_b + {\bf p_c})^2 = (E_b + E_c)^2 - E^2_b - E^2_c- 2 E_b E_c \cos \theta_{bc} \\ s = 2 E_b E_c ( 1 - \cos \theta_{bc}) = 4 E^2 x (1-x) \sin^2 \frac{\theta_{bc}}{2} \\ \sin \frac{\theta_{bc}}{2} = \sqrt{\frac{s}{4 E^2 x (1-x)}} \)\( donde \)x \in [0, 1]\(, siendo \)s = m^2_\pi = (0.135)^2\( GeV\)^2\( y \)E = 10$ GeV.
El valor mínimo de \(\theta_{bc}\) corresponde al máximo de \(x(1-x)\) que es \(x = 1/2\), esto es \(E_b = E_c = 5\) GeV
mpi = 0.135 ## GeV
E = 10 # GeV
def pi_theta(x, ss, E):
den = 4 * E**2 * x * (1 - x)
if (den == 0): return np.nan
return 2 * np.arcsin( np.sqrt(ss/den) )
xs = np.linspace(0., 1., 100)
thetas = [180 * pi_theta(xi, mpi*mpi, E)/ np.pi for xi in xs]
plt.plot(E * xs, thetas);
plt.xlabel(r'$E_b$ foton (GeV)'); plt.ylabel(r'$\theta_{bc}$ ($^O$)'); plt.grid();
theta_min = pi_theta(0.5, mpi*mpi, E)
print('theta min angle {:5.4f} rad, {:5.3f} degrees'.format(theta_min, 180*theta_min/np.pi))
theta min angle 0.0270 rad, 1.547 degrees
Por otro lado el valor mínimo de la energía, de la fracción \(x\), debe corresponder al máximo \(\theta = \pi, \sin^2 \theta/2 = 1\), por lo que:
$$ x(1-x) = \frac{s}{4E^2},;; x = \frac{1 - \sqrt{1 - s/E^2}}{2}
mpi = 0.135 # GeV
E = 10. # GeV
xmin = (1 - np.sqrt(1 - mpi*mpi/E**2))/2
print('minimum energy {:4.3f} keV'.format(E * xmin * 1e6))
minimum energy 455.646 keV
Otra forma de hacer el ejercicio es mediante las transformaciones de Lorentz.
En el sistema CM, los cuadrimomentos de los fotones son:
donde \(\theta^*\) es el ángulo respecto al eje \(z\).
En el sistema de laboratorio, los cuadrimomentos son: $\( p'_b = \frac{m_\pi}{2} \left(\gamma(1 + \beta \cos \theta^*), 0, \sin \theta^*, \gamma(\beta + \cos \theta^*) \right), \\ p'_c = \frac{m_\pi}{2} \left(\gamma(1 - \beta \cos \theta^*), 0, -\sin \theta^*, \gamma(\beta - \cos \theta^*) \right), \)$
En producto escalar de los momentos de los fotones en el sistema laboratorio es:
donde \(\gamma^2 = (1-\beta^2)^{-1}\)
Por otra parte: \({\bf p'}_{b} {\bf p'}_c = E_b E_c \cos \theta_{bc}\), así:
En este caso para \(\theta^* = \pi/2\) tenemos \(\theta_{bc}\) mínimo: $\( \cos \theta_{bc} = 2\beta^2 -1 \)\( Donde: \)\( \beta = \frac{p}{E} = \sqrt{1 - \frac{m^2}{E^2}} \)$
beta = np.sqrt(E**2 - mpi*mpi)/E
ctheta = 2*beta*beta -1
thetamin = np.arccos(ctheta)
print('theta min {:4.3f} rad, {:4.3f} degrees'.format(thetamin, 180 * thetamin / np.pi))
ctheta_bc = lambda theta: (2*beta**2 -1 - beta**2 * np.cos(theta)**2) / (1 - beta**2 * np.cos(theta)**2)
thetas = np.linspace(0, np.pi, 100)
plt.plot(thetas, np.arccos(ctheta_bc(thetas)));
plt.grid(); plt.xlabel(r'$\theta^*$ (rad)'); plt.ylabel(r'$\theta_{bc}$ (rad)');
theta min 0.027 rad, 1.547 degrees
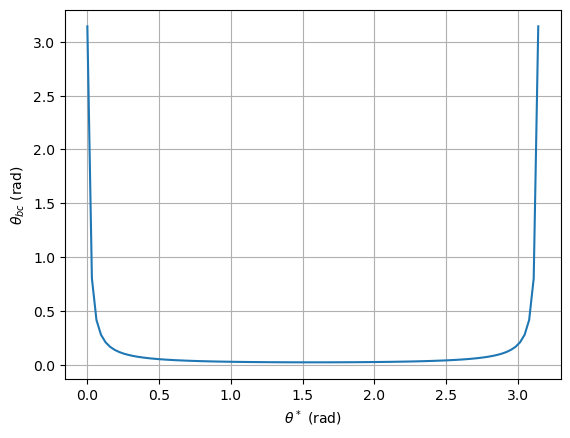
La energía mínima de \(E_c\) correspondera para el caso \(\theta^* = 0\).
emin = (mpi/2) * (E/mpi) * (1 - beta)
print('E foton min {:4.3f} KeV'.format(emin * 1e6))
E foton min 455.646 KeV