Sobre los leptones
Contents
3. Sobre los leptones#
import time
print(' Last version ', time.asctime() )
Last version Thu Oct 16 10:24:52 2025
# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2
# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.constants as units
3.1. Objetivos#
Los leptones sienten la fuerza electro-débil y se clasifican en tres familias que se comportan de forma universal.
Las corrientes cargadas presentan violación de carga y paridad.
La violación de paridad está asociada a la quiralidad de los espinores de Dirac.
Los neutrinos solo sienten la fuerza débil y al no tener masa, su helicidad y quiralidad son equivalentes.
Los neutrinos oscilan entre los distintos sabores al propagarse.
3.2. Características de los leptones#
Los leptones se presentan en tres generaciones agrupados en dupletes:
Sus propiedades:
\(e\) |
\(\mu\) |
\(\tau\) |
\(\nu\) |
|
|---|---|---|---|---|
masa |
0.511 MeV |
105.7 MeV |
1777 MeV |
\(\le\) 1 eV |
carga |
-1 |
-1 |
-1 |
0 |
vida media (\(\tau\)) |
estable |
\(2.197\) \(\mu\mathrm{s}\) |
\(290.6\) fs |
estable |
El electrón y el neutrino son estables.
Cuestión: ¿Cuál es el recorrido medio de un \(\mu\) o un \(\tau\) con momento \(p = 10\) GeV en el vacío?
Aplicando la transformación de Lorentz del tiempo propio del sistema en reposo al sistema del observador, obtenemos:
mass = 0.106 # GeV
tau = 2.2 * units.micro # s
p = 10 # GeV
ene = np.sqrt(mass**2 + p**2)
gamma = ene/mass
beta = p/ene
distance = gamma * beta * tau * units.c
print(' distance {:e} m'.format(distance))
distance 6.222108e+04 m
3.2.1. Desintegraciones#
La siguiente tabla muestra las desintegraciones principales de los leptones:
Fracción de desintegración |
|
|---|---|
\(\mu \to e + \bar{\nu_e} + \nu_\mu\) |
\(\sim 100\) % |
\(\tau \to \mu + \bar{\nu_\mu} + \nu_\tau\) |
\(17.4\) % |
\(\tau \to e + \bar{\nu_e} + \nu_\tau\) |
\(17.8\) % |
\(\tau \to \mathrm{hadrons}+ \nu_\tau\) |
\(\sim 64\) % |
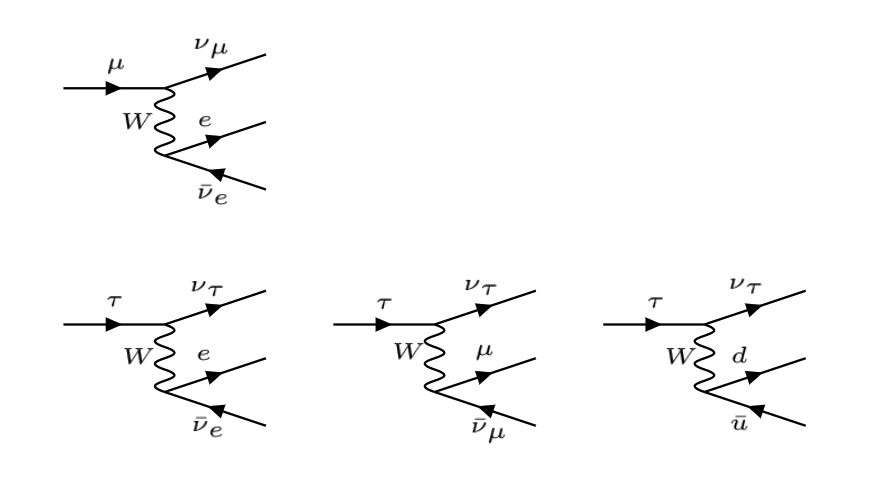
que corresponden a los siguientes diagramas de Feynman:
Desintegraciones del \(\mu\) (arriba) y del \(\tau\) (abajo) |
3.2.1.1. Conservación del número leptónico.#
Experimentalmente se observa que, en todas las interacciones conocidas, se conserva el número leptónico total, definido como el número de leptones menos el de antileptones.
Además, esta conservación se cumple independientemente en cada generación: electrónica, muónica y tauónica.
Por convenio, se asigna a cada leptón un número leptónico \(L=+1\) y a su antipartícula \(L=-1\), y de forma similar un número leptónico de sabor \(L_e, L_\mu, L_\tau\) según la siguiente tabla:
\(L_e\) |
\(L_\mu\) |
\(L_\tau\) |
\(L\) |
|
|---|---|---|---|---|
\((e, \nu_e), \; (e^+, \bar{\nu}_e)\) |
+1, -1 |
0 |
0 |
+1, -1 |
\((\mu, \nu_\mu), \; (\mu^+, \bar{\nu}_\mu)\) |
0 |
+1,-1 |
0 |
+1, -1 |
\((\tau, \nu_\tau), \; (\tau^+, \bar{\nu}_\tau)\) |
0 |
0 |
+1,-1 |
+1, -1 |
El número leptónico de sabor (por generación) y el total se conservan.
Cuestión: Verifica que el número leptónico de sabor y el total se conservan en las desintegraciones de \(\mu, \tau\).
Los experimentos que buscan violaciones del número leptónico sólo han logrado establecer límites inferiores a la vida media de los procesos que lo violarían, como en la búsqueda de la desintegración:
La conservación de la carga eléctrica garantiza que el electrón —la partícula cargada más ligera— sea estable.
Sin embargo, como veremos más adelante, las oscilaciones de neutrinos violan el número leptónico de sabor (electrónico, muónico o tauónico), aunque no el número leptónico total, y esta violación ocurre durante la propagación de los neutrinos.
Cuestión: ¿La desintegración \(\mu \to \nu_\mu + e + e^+\) viola alguna regla de conservación? ¿Y la desintegración \(\tau \to \mu + \mu + \mu^+\)?
3.2.2. Descubrimientos de los leptones#
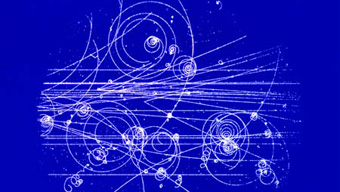
El 1932 C. Anderson descubrió el positrón en una cámara de burbujas en un campo magnético. Observó que de los productos con rayos cósmicos aparecían trazas que por su curvatura eran electrones pero con carga positiva.
En 1937 Aderson y Nedermayer descubrieron partículas penetrantes en los rayos cósmicos. En 1947 se observaron en emulsiones fotográficas con rayos cósmicos la desintegraciones del pión y del muón, que se correspondía a una partícula penetrante.
en 1975 M. Perl en el colisionador \(e^+e^-\) de SLAC descubrió el tau en la producción de pares \(e+e^+ \to \tau+\tau^+\), donde éstos se desintegraban leptónicamente \(\tau \to\mu +\bar{\nu}_\mu + \nu_\tau\)
En 1930, Wolfgang Pauli propuso —como una “solución desesperada”— la existencia del neutrino, una partícula neutra, fermiónica y de masa extremadamente pequeña, que escaparía a la detección experimental. Su hipótesis resolvía el enigma de la no conservación aparente de la energía y el momento en las desintegraciones \(\beta\).
En 1956, Frederick Reines y Clyde Cowan detectaron por primera vez el antineutrino electrónico \(\bar{\nu}_e\). Utilizando el intenso flujo de antineutrinos emitido por un reactor nuclear en Savannah River (Carolina del Sur), observaron la interacción beta inversa: \(\bar{\nu}_e + p \to e^+ +n \) empleando un detector con líquido centelleador y agua como blanco.
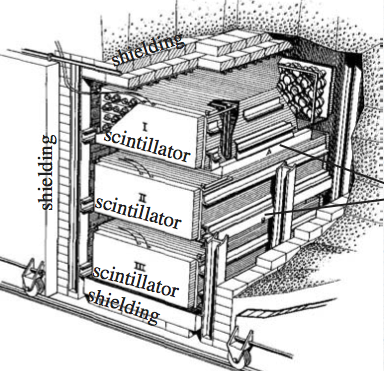
En 1962, Jack Steinberger, Leon Lederman y Melvin Schwartz descubrieron el neutrino muónico \(\nu_\mu\), utilizando un haz de neutrinos producido en el AGS de Brookhaven (Nueva York). Su detector, compuesto por capas alternadas de material pasivo y cámaras de chispas, permitió demostrar que los \(\nu_\mu\) son distintos de los \(\nu_e\), y que cada tipo de neutrino aparece emparejado con su leptón cargado correspondiente (\(e\) o \(\mu\)).
En 2001, la colaboración DONUT (Direct Observation of the NU Tau) en Fermilab observó por primera vez la interacción de un neutrino tauónico \(\nu_\tau\), mediante emulsiones fotográficas de alta resolución.
Otros hitos importantes relacionados con los neutrinos:
1956 — C. S. Wu y colaboradores realizan el experimento que demuestra la violación de paridad (\(P\)) en las desintegraciones beta del \(^{60}\mathrm{Co}\), confirmando la predicción de Lee y Yang.
1958 — M. Goldhaber, L. Grodzins y A. Sunyar determinan que el neutrino electrónico posee helicidad negativa, demostrando que es levógiro.
1970 — R. Davis y J. Bahcall identifican el llamado problema de los neutrinos solares, al observar un flujo de neutrinos procedentes del Sol muy inferior al predicho teóricamente.
1998 — T. Kajita y la colaboración Super-Kamiokande descubren las oscilaciones de neutrinos atmosféricos, demostrando que los neutrinos poseen masa y cambian de sabor.
2001–2002 — A. McDonald y la colaboración SNO (Sudbury Neutrino Observatory) resuelven el puzzle de los neutrinos solares, confirmando las oscilaciones y la conservación del número total de neutrinos.
3.2.3. Descubrimiento del neutrino#
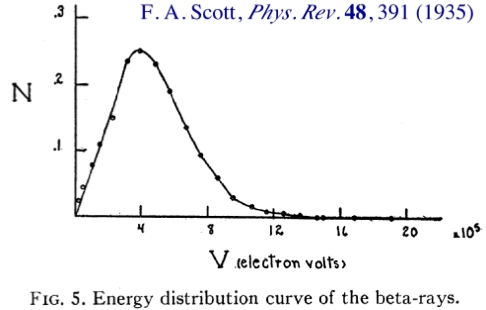
En la década de 1920, el espectro continuo de energía en las desintegraciones \(\beta\) se presentaba como un auténtico misterio.
Espectro \(\beta\) |
Si el núcleo padre se encuentra en reposo y sólo se emiten dos partículas —el núcleo hijo y el electrón \(\beta\)—, entonces el electrón debería ser monoenergético, de acuerdo con la conservación del momento. La energía total disponible para ambos productos es \(Q\), y en el sistema del centro de masas ambos son emitidos con el mismo momento \(p^*\).
La situación era tan desesperada que N. Bohr llegó a comentar: «At the present stage of atomic theory, however, we may say that we have no argument… for upholding the energy principle in the case of 𝛽-ray disintegrations.”
En 1930 Pauli postuó la existencia del neutrino en una histórica carta.
como un remedio desesperado para explicar el espectro continuo de energía en la desintegración \(\beta\) sugirió la existencia de una partícula neutra, fermiónica, penetrante, que escapase indetectada y que por lo tanto se llevase parte de la energía de la desintegración. Más tarde Fermi la denominaría neutrino.
Posteriormente B. Pontecorvo [>] sugirió utilizar el intenso flujo de neutrinos generado en los reactores nucleares para detectarlos mediante la interacción \(\beta\) inversa:
En 1956 F. Reines and C. L. Cowan confirmaron experimentalmente la existencia del neutrino utilizando esta reacción. Emplearon el flujo de antineutrinos, \(\phi_\nu \simeq 10^{17}\) \(\nu\mathrm{/(m^2 \, s)}\), generado en el reactor nuclear de Savannha River, CS, EE.UU.
cuestión: ¿Cuál es la energía que debe tener el \(\bar{\nu}_e\) para que ocurra esta interacción?
cuestión: Dibuja el diagrama de Feynman correspondiente.
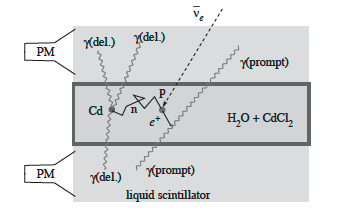
Detector Cowan-Reines |
Esquema de detección [AB2.6] |
El sistema de detección empleaba un conjunto de centelleadores sensibles a los fotones de 511 keV, producidos por la aniquilación del positrón, en coincidencia retardada con los fotones gamma generados en la captura del neutrón en núcleos de Cd.
Esta doble coincidencia caracterizaba inequívocamente el proceso de interacción beta inversa.
Reines y Cowan enviaron el siguiente telegrama a Pauli anunciándole el descubrimiento del neutrino:
telegrama anunciando el descrubrimiento del neutrino |
[Para esta sección ver AB2.2]
3.2.4. Universalidad leptónica#
La universalidad leptónica establece que la intensidad del acoplo en los vértices de las corrientes débiles cargadas es idéntica para las tres generaciones de leptones. En otras palabras, los leptones electrónicos, muónicos y tauónicos interactúan con la misma fuerza a través del bosón \(W^\pm\).
Vamos a comprobar, a partir de los datos experimentales, que esta igualdad de acoplos se cumple con gran precisión.
Para ello, supondremos que la constante de acoplo débil en cada vértice, denotada como \(g_W^\alpha\) con \(\alpha = e, \mu, \tau\), podría ser distinta para cada sabor leptónico, y contrastaremos esta hipótesis con los resultados experimentales.
La anchura de desintegración del \(\mu\), que se calcula en un curso más avanzado, es:
Cuestión: verifica que son correctas las dimensiones en la fórmula anterior.
Para la desintegración \(\tau \to e + \bar{\nu}_e + \nu_\tau\) intervendrán las constantes \(g^\tau_W\) en la corriente tauónica y \(g^e_W\) en la eléctrica.
La anchura de desintegración parcial es:
La anchura de desintegración total es la suma de las parciales y la fracción de desintegración, \(Br\), se relaciona con la anchura total y parcial por:
donde \(\tau_\tau\) es la vida media del \(\tau\).
Luego:
A partir de la razón entre las dos anchuras:
Podemos despejar la razón entre las constantes de cada sabor y sustituyendo por sus valores experimentales obtenemos:
Luego concluimos que hay una constante de acoplo para las dos familias \(g^\mu_W = g^\tau_W = g_W\).
tau_tau = 290.6 * units.femto # s
mass_tau = 1777 # MeV
tau_mu = 2.197 * units.micro # s
mass_mu = 105.7 # MeV
br_tau_e = 0.178
ratio = (tau_mu * mass_mu**5)/(tau_tau * mass_tau**5) * br_tau_e
print('Gamma ratio {:4.3f}'.format(ratio))
Gamma ratio 1.002
Recordemos que la constante de Fermi \(G_F\)
está relacionada con el intensidad del acoplo \(g_W\) del modelo estándar por:
donde \(m_W = 80.385 \pm 0.015\) GeV es la masa del \(W\).
Cuestión: A partir de las anchuras de desintegración \(\Gamma(\tau \to \mu + \nu_\mu + \bar{\nu}_\tau)\) y \(\Gamma(\tau \to e + \nu_e + \bar{\nu}_\tau)\) calcular \((g^e_W/g^\mu_W)^2\).
Nota: La desviación respecto de la unidad se compensa con un factor de espacio de fase.
[Para esta sección ver AB7.2]
3.3. Violación de Paridad#
Recordemos que la operación de inversión por paridad, \(P\), cambia:
y recordemos también cómo se clasifican distintas magnitudes bajo paridad:
Rango |
Paridad |
Ejemplo |
|
|---|---|---|---|
scalar |
0 |
+1 |
temperatura |
pseudo-scalar |
0 |
-1 |
helicidad |
vector |
1 |
-1 |
momento |
axial-vector |
1 |
+1 |
momento angular, campo magnético |
En la representación espinorial la representación de la paridad viene dada por la matriz \(\gamma^0\) [ver ext-trans-Lorentz]
3.3.1. El experimento de Wu#
En la década de los 50, Lee y Yang sospecharon que en las interacciones débiles podrían violar paridad. En 1957 Chien-Shiung Wu descubrió que las corrientes cargadas no conservan paridad.
Wu midió la dirección de la emisión de los electrones en la desintegración \(\beta\) de una muestra \(^{60}\mathrm{Co}\) a muy bajas temperaturas y bajo un campo magnético \({\bf B}\).
El \(^{60}\mathrm{Co}\) se desintegra \(\beta\):
Wu midió de electrones que salen hacia arriba cuando colocamos un campo magnético hacia arriba o hacia abajo.
Esquema de la desintegración \(\beta\) del \(^{60}\mathrm{Co}\) polarizado |
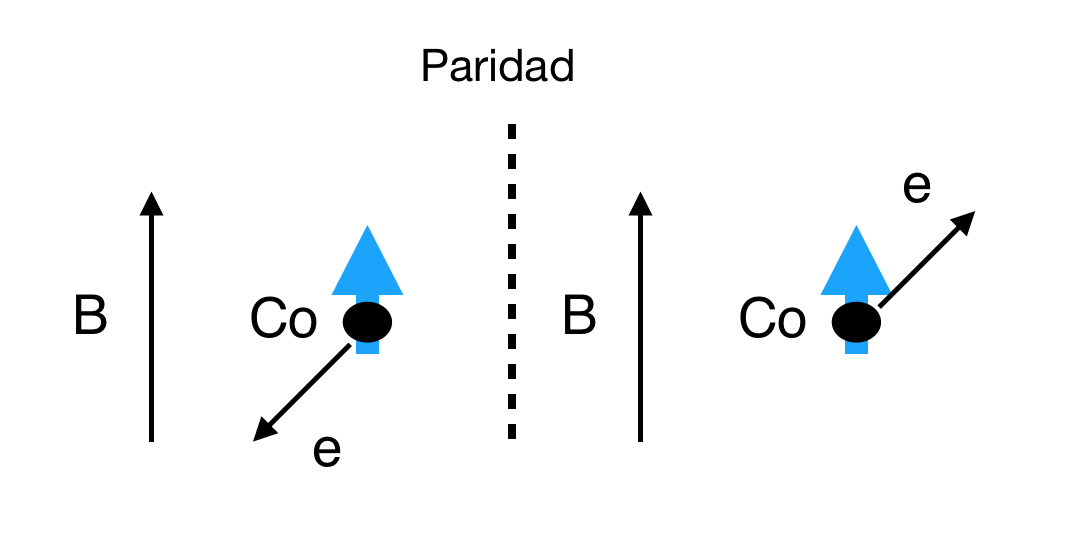
Decimos que un fenómeno viola paridad si el fenomeno reflejo en «el espejo» no sucede con la misma frecuencia que en el modelo. Considera el siguiente gráfico, la derecha es el reflejo de la izquierda.
Esquema de la desintegración \(\beta\) del \(^{60}\mathrm{Co}\) polarizado |
El nucleo de \(^{60}\mathrm{Co}\) tiene un momento magnético \({\bf \mu}\), dado por su espín, \({\bf S}\), que está alineado en la dirección de un campo magnético \({\bf B}\). Tanto \({\bf B}\), como \({\bf \mu}\) y \({\bf S}\), son vectores axiales, esto es, no cambian bajo paridad, mientras que el momento, \({\bf p}\), del electrón sí cambia por ser un vector.
Si se conserva la paridad, el electrón debe salir con igual frecuencia en el sentido de la imagen izquierda y en la derecha, esto es, con \(\theta\) respecto a la vertical y con \(\pi-\theta\). En el caso extremo, cuando el electrón sale en la vertical, el electrón sale con la misma probabilidad hacia arriba que hacia abajo.
En general los espines de los nucleos de una muestra están orientados en direcciones arbitrarias. Necesitamos primero alinearlos.
M. Wu fijó utilizó un campo magnético \({\bf B}\) para orientar la dirección de los espines de los núcleos (via su momento angular) en una dirección y colocó la muestra a muy bajas temperaturas para evitar que los espines vibrasen por los efectos térmicos.
Wu fijó la posición del detector y cambió de sentido el campo magnético, pero conceptualmente el experimento es equivalente al gráfico anterior.
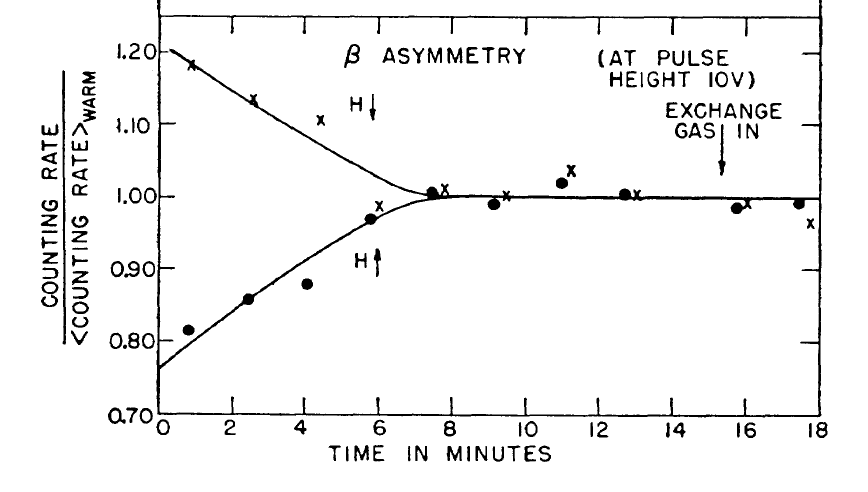
Razón de detección de \(e\) en función del tiempo y la polarización de \({\bf B}\) [WU] |
En la figura se muestran los resultados originales de Wu. Se observa que existe una asimetría arriba–abajo en función del tiempo. La asimetría está presente cuando los espines están alineados (mientras la muestra está fría) y se va perdiendo conforme los espines se desalinean (al perder el frío).
Se aprecia que los electrones se emiten preferentemente en el sentido opuesto al campo magnético, esto es, al del espín del Co. Los electrones salen hacia atrás.
Podríamos decir que el norte lo define el espín del núcleo, pero los electrones de los desintegración \(\beta\) prefieren dirigirse hacia el sur.
El experimento de Wu confirmó la predicción de Lee y Yang —quienes recibirían el Premio Nobel, injustamente sin incluirla a ella—: las desintegraciones \(\beta\) y, en general, las corrientes cargadas violan paridad.
Chien-Shiung Wu con su experimento (y ante el espejo) |
Cuestión: Observa las imágenes. La una es el espejo de la otra, pero solo una es real. ¿Cuál es la original y cuál su reflejo en el espejo? ¿Qué detalle te permite indentificar la imagen real?
3.3.2. Las corrientes bajo paridad#
La probabilidad de emisión del electrón en un determinado ángulo viene dada por la sección eficaz diferencial. Dado que la paridad no afecta a la parte cinemática de la sección eficaz, debe ser el elemento de matriz \(M_{fi}\) el que cambie bajo paridad.
Sin embargo, en la teoría de Fermi, el elemento de \(M_{fi}\) preserva paridad, dado que es proporcional al producto de dos corrientes, la hadrónica y la fermiónica:
Cada corriente cambia bajo paridad:
Y su producto es por lo tanto invariante.
cuestión: Aplicar paridad \(P\) sobre la corriente fermiónica \(\bar{\Psi} \gamma^\mu \Psi\).
La representación espinoral de la paridad es simplemente: \(P = \gamma^0\),
La corriente de probabilidad \(j^\mu = \bar{\Psi} \gamma^\mu \Psi\) bajo paridad se transforma a \({\bar \Psi} \gamma^0 \gamma^\mu \gamma^0 \Psi\), esto es:
por las propiedades de anticonmutación de las matrices \(\gamma^\mu\).
En este punto tenemos que introducir la matriz \(\gamma^5\):
que en la representación Pauli-Dirac es:
La matriz \(\gamma^5\) cumple las siguientes propiedades
cuestión: verifica las propiedades anteriores de \(\gamma^5\).
Todas las posibles formas bilineales en \(\Psi\) del tipo \(\bar{\Psi} \Gamma \Psi\), donde \(\Gamma\) son las posibles combinaciones independientes que podemos crear con las matrices \(\gamma^\mu\), son:
——– Forma ——– |
Componentes |
Spin |
|
|---|---|---|---|
scalar |
\({\bar \Psi} \Psi\) |
1 |
0 |
pseudo-scalar |
\({\bar \Psi} \gamma^5 \Psi\) |
1 |
0 |
vector |
\({\bar \Psi} \gamma^\mu \Psi\) |
4 |
1 |
pseudo-vector |
\({\bar \Psi} \gamma^\mu \gamma^5 \Psi\) |
4 |
1 |
tensor |
\({\bar \Psi} (\gamma^\mu\gamma^\nu - \gamma^\nu \gamma^\mu) \Psi\) |
6 |
2 |
En particular vemos que hay una forma \(\bar{\Psi}\gamma^\mu \gamma^5 \Psi\) que se comporta como un vector-axial. La presencia de la matriz \(\gamma^5\) cambia la forma escalar en pseudo-escalar y la forma vector (o corriente vectorial) en pseudo-vector (o corriente axial).
Para definir nuestro elemento de matriz \(M_{fi}\) podemos considerar ahora todas las combinaciones de las distintas formas que nos permitan obtener un invariante escalar Lorentz.
A partir del estudio de las desintegraciones de los muones \(\mu \to e + \nu_\mu + \bar{\nu}_e\) se determinó qué formas intervienen en el acoplo de las corrientes débiles cargadas.
Espectro de energía del electrón en \(\mu\) decays, la línea es la teoría V-A [MU] |
La forma fenomenológica que corresponde a las desintegraciones de muones (y las corrientes cargadas) es:
Esto es, intervienen dos corrientes:
La corriente \(j^\mu_V = \frac{1}{2}{\bar \Psi} \gamma^\mu \Psi\) es vectorial porque cambia como un vector frente a paridad.
La corriente \(j^\mu_A = \frac{1}{2}{\bar \Psi} \gamma^\mu \gamma^5 \Psi\) es axial porque cambia como un axial-vector frente a paridad.
Por eso decimos que las corrientes cargadas tienen una estructura \(V-A\)
¿Cómo cambia ahora \(M_{fi}\) bajo paridad?
Y ahora \(M_{fi}\), al ser el producto de dos corrientes \(V-A\), sí que cambia bajo paridad:
3.3.3. La quiralidad#
En vez de ver la interacción como corrientes \(V-A\) podemos preguntarnos ¿qué es el término \(\frac{1}{2} (I-\gamma^5)\) que aparece en \({\bar \Psi} \gamma^\mu \frac{1}{2}(I - \gamma^5) \Psi\)?
Podemos observar que es un proyector que actua sobre el espinor de Dirac:
Existen dos proyectores complementarios:
que cumplen las condiciones de proyectores:
Estos proyectores se llaman de quiralidad y proyectan el espinor a izquierda y derecha.
Cuestión: Verifica que \(P_L, P_R\) cumplen las condiciones anteriores.
Los llamamos proyectos de quiralidad porque un proyector se transforma en el otro al aplicarle la inversión de paridad.
La representación espinorial de la paridad es la matriz \(P \equiv \gamma^0\), la transformación de de paridad de \(P_L\) es:
De tal forma que un espinor de Dirac se descompone en dos proyecciones, de quiralidad a izquierdas y derechas:
que se invierten al aplicar paridad:
decimos que una es el reflejo de la otra.
La quiralidad es una propiedad de los espinores. Matemáticamente la quiralidad corresponde a los autovalores de la matriz \(\gamma^5\).
\(\Psi_{R/L}\) son autoestados con autovaloes \(+1, -1\) respectivamente de \(\gamma^5\).
En general, cuando hablamos solo de espinores solemos habitualmente omitir la fase de \(\Psi_{L/R}\), y escribimos principalmente la parte puramente espinorial \(u_{L/R}\)
Nota
Ya vimos que el espinor de Dirac presenta un comportamiento frente a las rotaciones que desafía nuestra intuición clásica. Al girarlo \(2\pi\), el espinor cambia de signo; sólo tras un giro completo de \(4\pi\) recupera su estado inicial.
Es el mismo tipo de paradoja visual que encontramos en la hormiga de Escher recorriendo la cinta de Möbius: tras recorrer una vuelta, la hormiga se encuentra boca abajo y tiene que recorrer la cinta dos veces para regresar a su posición inicial.
Nota
Cinta de Möbius (izquierda) |
Cinta de Möbius (derecha) |
De forma análoga, una cinta de Möbius puede construirse en dos versiones quirales: una obtenida al unir los extremos de una tira con un giro hacia la izquierda, y la otra con un giro hacia la derecha. Cada una es la imagen especular de la otra, pero no pueden superponerse mediante rotaciones en el espacio tridimensional.
Así como las dos cintas de Möbius están relacionadas por una reflexión, las dos componentes del espinor —izquierda y diestra— se conectan a través de la operación de paridad.
ejercicio: Verifica que:
Puedes verificar previamente que:
3.3.3.1. La quiralidad en las interacciones débiles#
Podemos decir de forma equivalente que las corrientas cargadas
son de tipo V-A, \(\; {\bar \Psi} \, \frac{1}{2}\gamma^\mu (I - \gamma^5) \, \Psi\)
o en ellas, solo intervienen los espinores a izquierdas de los fermiones, \(\Psi_L = \frac{1}{2} (I - \gamma^5) \, \Psi\), y de derechas a los anti-fermiones.
Una teoría que viole paridad favorece una quiralidad respecto a la otra.
Nota
Podemos usar un simil con las cartas de juego de naipes para comprender el efecto de la quiralidad y la inversión de paridad.
Las cartas tienen dos caras, la de la figura y el reverso, similar a los espinores que tienen quiralidad a izquierdas y a derechas. La inversión de cara nos da la vuelta a la carta. La inversión por paridad nos cambia la quiralidad de espinor.
Un juego de cartas invariante respecto a la inversión de caras sería por ejemplo simplemente contarlas. Podemos lanzar las cartas sobre la mesa y contarlas, da igual que estén boca arriba que boca abajo. Nada cambia si revertimos cada una de las cartas. Algo muy aburrido. Los juegos habituales de cartas sí violan la inversión de caras porque solo usamos la cara de la figura, ¡Ahí está parte de la diversión!
Algo así sucede en la Naturaleza, los espinores tienen dos quiralidades, la inversión de paridad invierte la quiralidad. En las interacciones débiles y fuertes no hay distinción de las quiralidades de los espinores, preservan la paridad, pero sí hay distinción en las interaciones débiles. En las corrientes débiles cargadas (mediadas por \(W^\pm\)) solo participan los espinores a izquierdas de las partículas y los de derechas de las antipartículas, esto es, se viola paridad de forma máxima.
Nota
Los físicos del siglo XX utilizaron definiciones que llevan a la confusión, como el abuso de los diversos «isoespins», pero especial cuiado hay que tener de no confundir la helicidad con la quiralidad.
Otro punto de confusión, viene dado porque cuando trabajamos con espinores directamente (esto es, no trabajamos directamente en TCQ), el resultado físico de algunos operadores sobre las antipartículas requiere invertir el signo, como es de nuevo el caso para la quiralidad. Para la parte espinorial de las antipartículas \(v_R\)
Desafortunadamente, de esta forma, la proyección de quiralidad a derechas del espinor \(v\) viene dada por:
3.3.4. Helicidad y quiralidad#
Aunque helicidad y quiralidad no son lo mismo, hay un caso muy relevante, donde coinciden.
Recordemos que la helicidad es la proyección del espín en la dirección del momento de la partícula.
En la representación de Pauli-Dirac, los proyectores de quiralidad son simplemente:
Sean ahora los espinores de helicidad \(\pm\) con \({\bf p} = p \, \hat{k}\) en la dirección \(z\):
donde \(N\) es un factor de normalización y:
Si aplicamos los proyectores de quiralidad sobre los espinores \(u_{\pm}\) de helicidad, obtenemos:
Obtenemos así la tabla con los coeficientes de las componentes de quiralidad y de helicidad de los espinores \(u\) de cada helicidad:
helicidad \(\downarrow\) \ quiralidad \(\rightarrow\) |
— R — |
— L — |
|---|---|---|
+ |
\(\frac{1}{2}(1+\kappa)\) |
\(\frac{1}{2}(1-\kappa)\) |
- |
\(\frac{1}{2}(1-\kappa)\) |
\(\frac{1}{2}(1+\kappa)\) |
en los acoplos con el \(W\) |
anti-fermiones, \(v_R\) |
fermiones, \(u_L\) |
Hemos dicho que en la interacciones débiles cargadas solo participan los espinores \(u_L\), esto es la última columna, L.
Si repitiésemos los cálculos para los espinores \(v_R\) obtendríamos los mismos coeficientes. En las corrientes débiles entraría la parte \(v_R\) que correpondería a la columna del medio, R.
Consideremos ahora el caso de partículas sin masa, \(m=0\), o ultra-relativistas, \(m \ll E\), en ambos casos tenemos que \(\kappa = 1\) y por lo tanto:
helicidad \(\downarrow\) \ quiralidad \(\rightarrow\) |
— R — |
— L — |
|---|---|---|
+ |
1 |
0 |
- |
0 |
1 |
en los acoplos con el \(W\) |
anti-fermiones, \(v_R\) |
fermiones, \(u_L\) |
Esto es para partículas sin masa o ultra-relativistas la quiralidad y la helicidad coinciden.
En esos dos casos -que son los más comunes a altas energías- solo participan en la corrientes cargadas los espinores de los fermiones \(u_-\) con helicidad negativa y de los antifermiones \(v_+\) con helicidad positiva.
3.4. El neutrino en la corrientes cargadas#
3.4.1. Helicidad del neutrino#
En 1957, Maurice Goldhaber y sus colaboradores midieron en el laboratorio de Brookhaven (Nueva York, EE. UU.) la helicidad del neutrino, descubriendo que es siempre negativa. Este constituye uno de los experimentos más ingeniosos y sutiles de la historia de la Física de Partículas.
Goldhaber estudió la emisión de fotones en la siguiente captura electrónica:
Para ello emplearon un material inusual: europio radiactivo, cuyos electrones de captura fueron polarizados mediante un campo magnético externo. El diseño experimental garantizaba que neutrinos y fotones se emitieran preferentemente a lo largo de la dirección vertical.
Inicialmente, el núcleo de europio posee momento angular total nulo. Tras la captura electrónica, el núcleo de samario queda excitado con momento angular \(J=1\) y decae casi de inmediato a su estado fundamental (\(J=0\)), emitiendo un fotón gamma de espín 1.
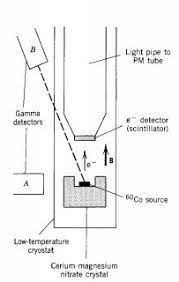
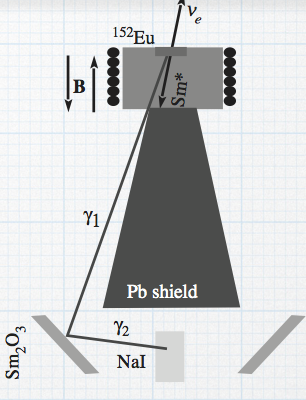
Esquema del experimento de Goldhaber [GOL] |
Goldhaber midió el número de fotones emitidos —proporcional al número de capturas electrónicas— en una dirección y sentido determinados (en este caso, hacia abajo), para dos orientaciones opuestas del campo magnético: hacia arriba y hacia abajo.
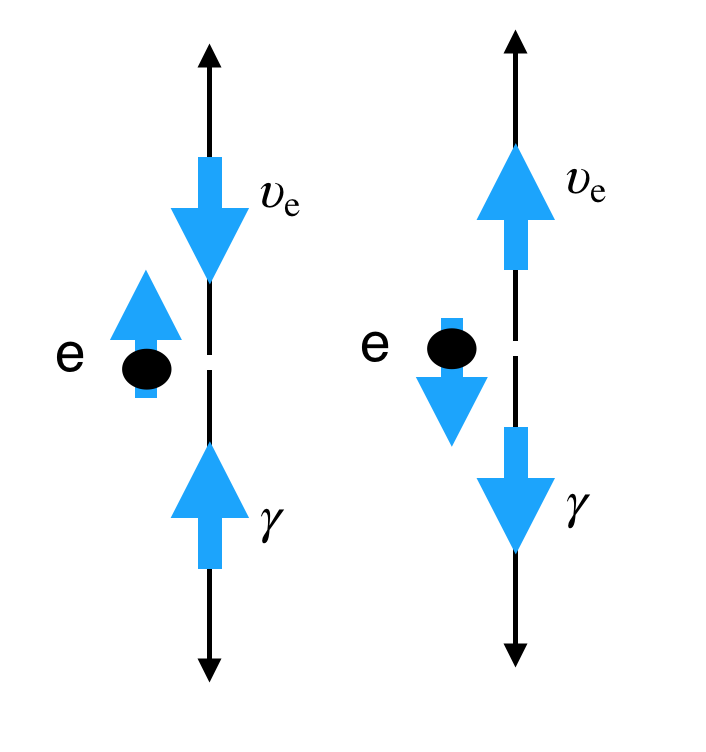
En el esquema de la siguiente figura se muestra el electrón inicial con su espín polarizado en ambas direcciones, así como la emisión del neutrino y del fotón a lo largo del eje vertical. También se representan sus espines y, por tanto, la helicidad correspondiente de cada partícula.
helicidades en el experimento de Goldhaber |
La dirección \(z\) se define como la “vertical” del experimento, determinada por el eje del campo magnético \({\bf B}\), que polariza al electrón procedente de la captura de \(^{152}\mathrm{Eu}\) hacia arriba o hacia abajo, con \(S_z(e) = \pm \tfrac{1}{2}\) según la orientación del campo.
Se seleccionan los fotones que se emiten hacia abajo, y la configuración experimental garantiza que el neutrino correspondiente se emite hacia arriba. La tercera componente del espín, \(S_z = \pm \tfrac{1}{2}\), se conserva en el proceso, lo que implica que la helicidad del neutrino coincide con la del fotón emitido.
Si se observara el mismo número de fotones en ambas configuraciones, el neutrino poseería las dos helicidades posibles. En cambio, si una de las configuraciones domina, significaría que el neutrino tiene una helicidad preferente.
El resultado del experimento de Goldhaber demostró que los neutrinos poseen solo helicidad negativa, es decir, la proyección de su espín sobre la dirección del momento es siempre opuesta a este.
La siguiente tabla muestra las posibilidades de espín y helicidades posibles en el experimento de Goldhaber.
—– \(S_z(e)\) —– |
—– \(S_z(\nu)\) —– |
—– \(S_z(\gamma)\) —– |
—– \(h(\nu)\) —– |
—– \(h(\gamma)\) —– |
observación |
|---|---|---|---|---|---|
1/2 |
-1/2 |
1 |
- |
- |
si |
-1/2 |
1/2 |
-1 |
+ |
+ |
no |
En la Naturaleza solo se observa la primera posibilidad: existen únicamente neutrinos con helicidad negativa; los de helicidad positiva no se producen.
Ya vimos que, para una partícula sin masa, helicidad y quiralidad coinciden, de modo que el hecho de que los neutrinos tengan helicidad negativa implica que poseen quiralidad a izquierdas.
Este resultado está íntimamente ligado al principio fundamental de que las interacciones débiles cargadas solo actuan sobre fermiones con quiralidad a izquierdas (y sobre antifermiones con quiralidad a derechas).
3.4.2. La masa del neutrino#
Los experimentos que han intentado medir directamente la masa del neutrino solo han conseguido establecer límites superiores a su valor.
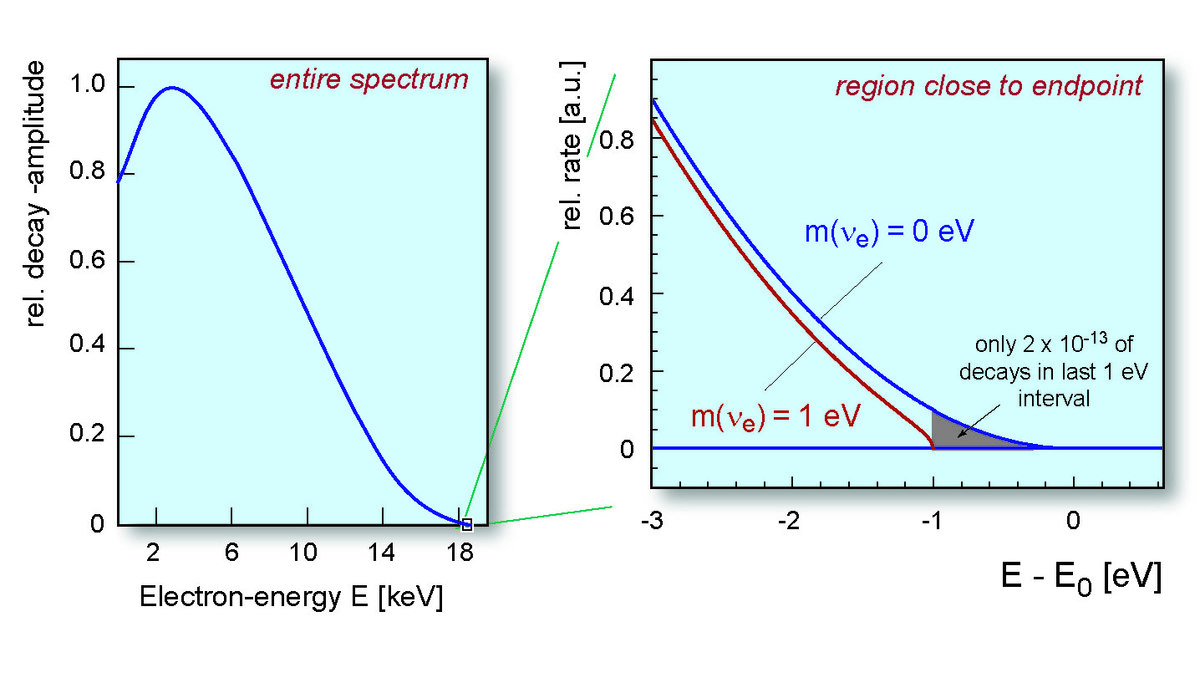
La masa del neutrino se busca a partir de la distorsión en el extremo final del espectro de energía del electrón en la desintegración \(\beta\) del tritio:
Espectro de energía del electrón de la desintegración del tritio si el neutrino tiene una masa \(\sim\) 1 eV |
Si el neutrino posee masa, el electrón no puede llevarse toda la energía disponible en la desintegración, por lo que el extremo final del espectro de energía del electrón se ve modificado de forma dependiente de la masa del neutrino.
El experimento KATRIN, actualmente en operación, ha establecido el límite más bajo hasta la fecha para la masa del neutrino:
¡El neutrino es -al menos- un millón de veces más ligero que el electrón!
3.4.3. Espinores de Weyl#
Vamos a ver que el espinor de Dirac de los neutrinos —si éstos no tienen masa— puede descomponerse en dos bi-espinores independientes, llamados espinores de Weyl, cada uno con una quiralidad distinta.
Utilizaremos para ello la representación de Weyl (o quiral) de las matrices de Dirac:
De esta forma, los operadores de proyección de quiralidad son:
cuestión: Verifica que la matrices de la representación de Weyl cumplen las condiciones de las matrices \(\gamma^\mu\).
En esta representación, el espinor de Dirac está formado de dos bi-espinores, \(u_L, u_R\), llamados de Weyl, que corresponden con la parte de quiralidad a izquierdas y a derechas del espinor de Dirac.
Podemos comprobar que las proyecciones de quiralidad son:
Y que la paridad intercambia las quiralidades
Si ahora consideramos el caso revelador de un fermión sin masa \(m=0\), la ec. de Dirac se reduce a:
Y se descompone en dos ecuaciones independientes para los bi-espinores de quiralidad derecha e izquierda:
Es decir, el espinor de Dirac se separa en dos espinores de Weyl independientes, cada uno con una quiralidad definida.
Dado que para una partícula sin masa se cumple \(E = p\), donde \(\mathbf{p} = p, \hat{\mathbf{v}}\), las ecuaciones anteriores pueden escribirse como:
Es decir, existe una correspondencia uno a uno entre helicidad y quiralidad para los fermiones sin masa: el espinor de Weyl de quiralidad izquierda posee helicidad negativa, y el de quiralidad derecha, helicidad positiva:
En este caso, quiralidad y helicidad son propiedades equivalentes.
Además, los bi-espinores de Weyl son completamente independientes, ya que la ecuación de Dirac se separa en dos ecuaciones desacopladas, una para cada quiralidad.
3.4.4. El neutrino en el Modelo Estándar#
El Modelo Estandar postula que el neutrino no tiene masa, lo que implica que sus espinores de quiralidad a izquierdas y derechas son independientes.
Los neutrinos solo interaccionan débilmente, y en las interacciones débiles solo intervienen las proyecciones a izquierdas, esto es \(u_L\) y \(v_R\). Solo son reales esos dos espinores para el neutrino:
En términos de la conjugación de Carga y Paridad encontramos:
\(\hat{P}\) |
|||
|---|---|---|---|
\(\nu_L\) |
\(\Rightarrow\) |
\(\nu_R\) (no existe) |
|
\(\hat{C}\) |
\(\Downarrow\) |
\(\Downarrow\) |
|
\(\bar{\nu}_L\) (no existe) |
\(\Rightarrow\) |
\(\bar{\nu}_R\) |
La fuerza débil viola de forma máxima paridad, \(P\), y conjugación de carga, \(C\), pero no \(CP\).
Dado que el neutrino:
tiene masa compatible con nula.
la helicidad es negativa (para el anti-neutrino positiva).
El Modelo Estándar postula que los neutrinos no tienen masa, solo existen en quiralidad a izquierdas, y el antineutrino con quiralidad a derechas,
Las corrientes cargadas en leptones violan paridad, P, y carga, C; pero preservan CP
Efecto de aplicar paridad (reflejo, izquierda-derecha) y carga (invertir grises, arriba-abajo) en un dibujo inicial de M.C. Escher.
Nota
Los físicos de partículas se sintieron reconfortados -aunque solo por un breve periodo- al comprobar que, si bien la inversión por paridad, \(P\) y la inversión por carga, \(C\), se violaban, la combinación conjunta \(CP\) se conservaba.
En aquella época, a mediados del siglo XX, cuando los extraterrestres estaban de moda, Feynman se hacía la siguiente pregunta:, ¿Cómo podría estar seguro de estrechar la mano de un alienígena que quizás estuviese compuesto solo de antipartículas?
Y él mismo se respondía: le pediría que repita el experimento de Ms. Wu, que me diga la dirección privilegiada hacia donde salen los electrones de su mundo en una desintegración \(\beta\) respecto al espín del núcleo. Si en su mundo, como en el nuestro, salen en la dirección opuesta le doy la mano, si salen en la misma… mejor no.
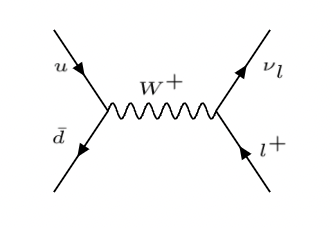
3.5. Desintegración del pión#
Diagrama de Feynman de \(\pi^+ \to l^+ + \nu_l\) |
La desintegración del pión \(\pi^+ \to l^+ + \nu_l\) ejemplifica los efectos de la estructura V-A de las corrientes cargadas.
La razón de las anchuras de desintegración a \(l = \mu, e\) experimental es:
Sin embargo el espacio fásico disponible para el \(e\) es mayor que el del \(\mu\) dado que la razón entre ellos viene dada por \(p^*_e/p^*_\mu\), y el momento \(p^*_e > p^*_\mu\).
¿Por qué entonces el \(\pi^+\) se desintegra principalmente a \(\mu^+\) y no \(e^+\)?
Cuestión: Calcula \(p^*_l, E^*_l\) en el CM.
Cuestión: Calcula la razón entre el \(p^*_e/p^*_\mu\).
En el CM $\( E_l = \frac{m^2_\pi + m^2_l}{2 m_\pi}, \; \; p_l = \frac{m^2_\pi - m^2_l}{2 m_\pi} \)$
mpi = 139.51 # MeV
mmu = 105.66 # MeV
me = 0.511 # MeV
ene_cm = lambda ml : (mpi**2 + ml**2)/(2*mpi)
p_cm = lambda ml : (mpi**2 - ml**2)/(2*mpi)
a_R = lambda ml : (1 - p_cm(ml)/(ene_cm(ml) + ml))/2
beta_mu, beta_e = p_cm(mmu)/ene_cm(mmu), p_cm(me)/ene_cm(me)
espace_phase = p_cm(me)/p_cm(mmu)
print(' beta mu = {:7.6f} , beta e = {:7.6f} '.format(beta_mu, beta_e))
print(' energy mu = {:5.3f} MeV, energy e = {:5.3f} MeV'.format(ene_cm(mmu), ene_cm(me)))
print(' espacio fásico = {:e}'.format(espace_phase))
beta mu = 0.270970 , beta e = 0.999973
energy mu = 109.767 MeV, energy e = 69.756 MeV
espacio fásico = 2.345194e+00
Vemos que el \(\mu\) no es relativista, \(\beta = 0.27\), pero sí el electrón, \(\beta = 0.99997\).
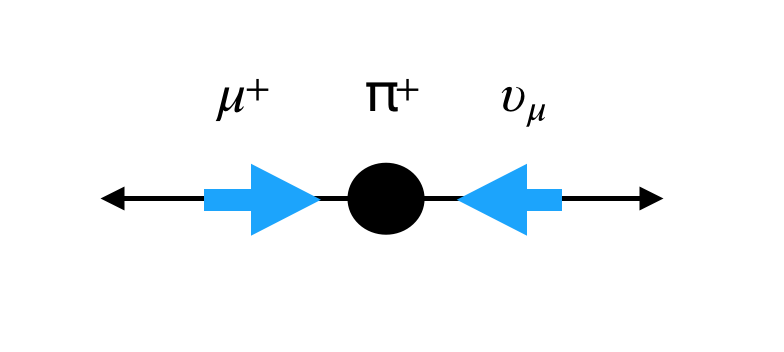
Revisemos ahora la helicidad de las partículas de la desintegración.
Momento y spin de \(\pi^+ \to l^+ + \nu_l\) en el CM |
En el CM, el \(\pi^+\) tiene spín nulo, el neutrino, \(\nu_l\), tiene necesariamente helicidad (-) y es a izquierdas \((L)\), y para conservar el momento angular, el anti-leptón cargardo, \(l^+\) debe tener helicidad (-). La proyección del momento del espín del anti-leptón cargado es opuesta a la del neutrino para que la suma total del espín sea nula.
Por otro lado, sabemos que solo la proyección con quiralidad a derechas de los anti-leptones interviene en la desintegración. ¿Cuánto el coeficiente asociado a esa proyección para el \(e^+\) y el \(\mu^+\)?
Recordemos que el espinor \(v_-\) con helicidad (-) tiene como coeficiente de quiralidad a derechas:
A partir de la \(E_l, p\) en el CM, obtenemos:
El factor \((1-\kappa)/2\) es mucho más pequeño para \(e\) que para el \(\mu\).
El factor asociado a las proyecciones a derechas entre el \(e\) y \(\mu\) que aparece en \(|M_{fi}|^2\) será:
La desintegración de \(\pi^+\) a \(e^+\) está muy suprimida porque la componente de quiralidad a derechas del \(e^+\) está muy suprimida para un \(e^+\) de helicidad negativa. En este caso, el hecho de que el electrón es relativista y la conexión helicidad-quiralidad es la razón por la que esta desintegración está muy suprimida.
De esta forma, la preponderancia de la desintegración del \(\pi^+\) a \(\mu^+\) se explica por la naturaleza \(V-A\) de las interacciones débiles cargadas.
helicity_supres = a_R(me)/a_R(mmu)
print(' supresion por helicidad = {:e}'.format(helicity_supres**2))
print(' total = {:e}'.format(espace_phase * helicity_supres**2))
supresion por helicidad = 7.170821e-05
total = 1.681697e-04
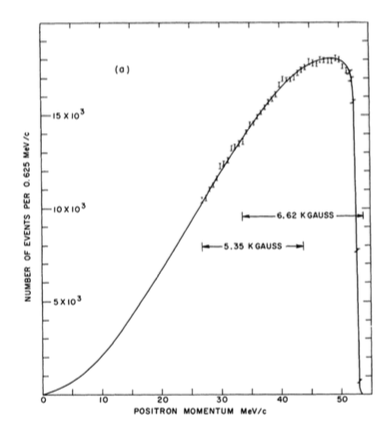
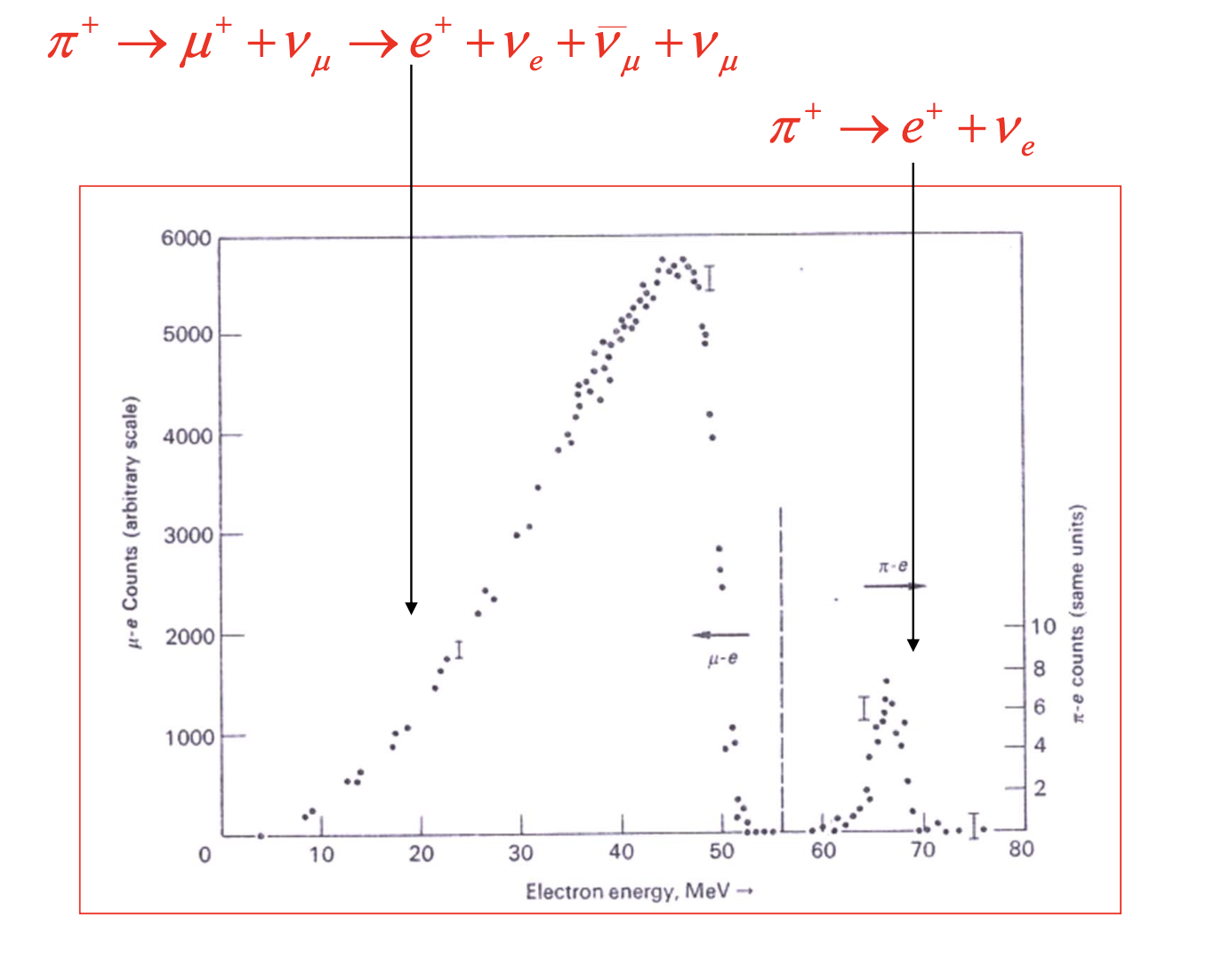
En la siguiente distribución de la energía del espectro de electrones en las desintegraciones del \(\pi^+\).
Espectro de energías del \(e\) en las desintegraciones del \(\pi\) [AB] |
Puede observarse que la desintegración de \(\pi\) a \(e\) está suprimida (hay menos eventos en la distribución), también que el electrón es monoenergético (su energís es un pico); mientras que aquellos electrones que provienen de la desintegración del \(\mu\) son más abundantes y presentan una distribución continua en energía.
[Para esta sección ver MT11.2.3, MT11.6, AB7.3, AB7.4, AB7.5]
3.6. Oscilaciones de neutrinos#
Sabemos experimentalmente que los neutrinos oscilan entre sus sabores en su propagación.
Las oscilaciones dependen de las masas de los neutrinos.
Pero recordemos que el Modelo Estándar postula que los neutrinos no tienen masas.
Esto hace que las oscilaciones de neutrinos sean por ahora la única prueba experimental de que el SM necesita revisarse.
3.6.1. El puzzle solar#
En la década de los 60, el experimento de R. David en la mina de Homestake, Dakota del Sur, midió el flujo de \(\nu_e\) solares y resultaba ser \(1/3\) del esperado según el modelo teórico del Sol desarrollado por J. Bahcall.
Durante aproximadamente 40 años los resultados de los experimentos que medían el flujo de \(\nu_e\) solares mostraban un deficit respecto al flujo esperado según el modelo solar.
En el 2004 El experimento SNO (en Canada) midió el flujo total (la suma de los flujos de los diferentes sabores) de neutrinos y verificó que estaba en acuerdo con el esperado por el modelo solar para los neutrinos, todos \(\nu_e\), producidos en el Sol. Por lo tanto los neutrinos que llegan a la tierra corresponden con los emitidos del Sol, solo que allí se producen como \(\nu_e\) y en la Tierra se detectan solo 1/3 con ese sabor, el 2/3 restante cambia de sabor.
Pontecorbo en los 50’s adelantó que los neutrinos podrían oscilar entre sus diversos sabores si tenían masas distintas.
3.6.2. Neutrinos atmosféricos#
En 1998 el experimento Super-Kamiokande en la mina de Kamioka, Japón, midió que el flujo de \(\nu_\mu\) producido en las interacciones de los rayos cósmicos con la atmósfera dependía de la dirección de llegada, en concreto midió que existía una asimetría arriba y abajo, donde abajo correspondía a los neutrinos que habían atravesado la Tierra, y arriba sólo la atmósfera.
Ahora sabemos que los \(\nu_\mu\) dependiendo de la distancia recorrida se transforman de sabor a los dos otros neutrinos, pero principalmente en \(\nu_\tau\).
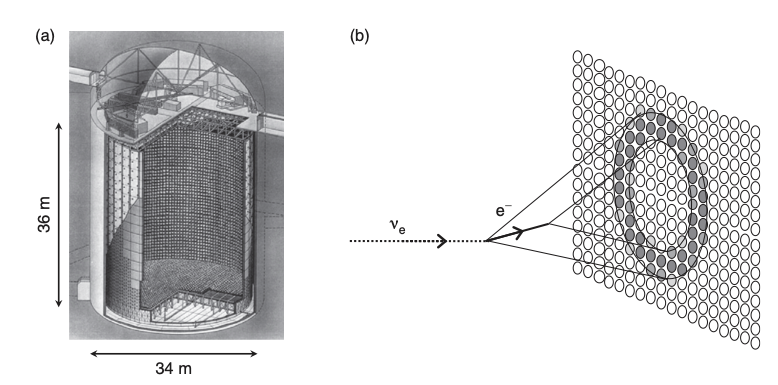
La siguiente figura muestra el detector Super-Kamiokande.
Super-Kamiokande a) dibujo del detector b) principio de detección [SK, MT13.2] |
SK es un tanque de agua de 50 kton, 36 m de altura y 34 de diámetro, con 11 k PMTs en las paredes.
SK detecta las corrientes cargadas de neutrinos \(\nu_e \to e + X\) o \(\nu_\mu \to \mu + X\), a partir del leptón cargado.
En el agua, el leptón a partir de un umbral de energía emite luz Cherenkov, en forma de cono, que se detecta en gigantescos PMTs colocados en las paredes del detector.
A partir de la luz y el tiempo de de su llegada a los PMTs se determina la energía y dirección del neutrino.
Se pueden distingir \(e\) de \(\mu\) por los patrones de luz en los PMTs.
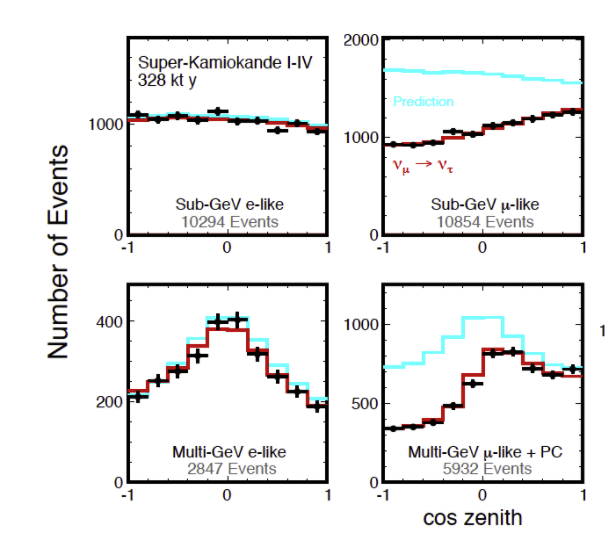
Resultados de la colaboración SK.
eventos de \(\nu_e\) (izda), \(\nu_\mu\) (dcha) detectados por SK en función del ángulo [SK] |
En la figura, el eje \(x\), correponde al \(\cos \theta\), donde \(\theta\) es el ángulo de llegada, \(\cos \theta = 1\) indica arriba, y \(\cos \theta = -1\), abajo (o sea, atravesando la Tierra).
Observamos:
Para los \(\nu_e\) la predicción y la observación coinciden.
Para los \(\nu_\mu\), de multi-GeV, hay un déficit para aquellos que provienen de “abajo”.
La línea corresponde a las predicción en caso de oscilaciones.
Luego SK concluyó que los neutrinos producidos \(\nu_\mu\) en las atmósfera oscilan en su recorrido hasta el detector.
3.6.3. Oscilaciones en dos familias#
Como los neutrinos son neutros, un neutrino de un sabor, por ejemplo \(\nu_e\), puede estar compuesto por una combinación de neutrinos con diferentes masas.
Cada neutrino se propagará libremente de acuerdo con su masa como una onda libre; y con la distancia -o el tiempo transcurrido-, la composición inicial de los diferentes tipos de neutrinos cambia.
Los neutrinos pueden oscilar si los estados de sabor no son los mismos que los estados de masas y las masas de los neutrinos son distintas.
Los estados de sabor son \(\nu_\alpha\), con \(\alpha = e, \mu, \tau\), y los estados de masas \(\nu_i\) con masas \(m_i\) donde \(i = 1, 2, 3\).
Consideremos por simplicidad solo dos sabores y dos masas. Los sabores serán: \(\alpha, \beta\)
La relación entre estados de masas y de sabor de neutrinos viene dada por una matriz de mezcla:
Si producimos un neutrino de un determinado sabor, \(\nu_\alpha\), en un tiempo \(t_0 = 0\), con un momento \(p\), este es una combinación de los neutrinos de masas \(| \nu_1 \rangle, \, | \nu_2 \rangle\) que depende de un ángulo \(\theta\).
La evolución de cada neutrino de masas corresponde a la de una partícula libre, esto es:
donde \(E_i = \sqrt{m^2_i + p^2}\), con \(i = 1, 2\)
En un determinado tiempo \(t\), o equivalentemente a una distancia \(L\), podemos detectar el neutrino con otro sabor \(\beta\).
¡Recordemos que las interacciones de los neutrinos tienen lugar en sus estados de sabor!
Calculamos la amplitud de transición:
recordemos que una fase global en la amplitud, en este caso \(e^{i{\bf px}}\) no afecta a la física del proceso.
Si operamos:
$\(
A_{\alpha\beta}(t) = \frac{1}{2}\sin 2 \theta e^{-iE_1} \left( 1 + e^{-i(E_2 - E_1)t}\right)
\)$
de nuevo la fase global \(e^{-iE_1t}\) no altera la física, y si desarrollamos:
donde \(\Delta m_{21}^2 = m_2^2 - m^2_1\), y dado que \(m_i \sim 0\) aproximamos \(p \sim E\)
La probabilidad de aparición, o de oscilación, de un \(\nu_\alpha\) como \(\nu_\beta\) a un tiempo \(t\) es:
Podemos dar la probabilidad de oscilación a una distancia \(L\), que corresponde a tiempo, \(t\).
Notar que los experimentos se situan a una distancia \(L\) de la fuente de neutrinos.
Si damos unidades:
Se trata de una probabilidad de forma oscilatoria, cuya amplitud están controlada por \(\theta\), si \(\theta = 0\) no hay oscilación, y su frecuencia por \(\Delta m^2_{21}\), si los dos neutrinos tienen igual masa, tampoco hay oscilación.
En la fórmula anterior hay dos parámetros físicos, \(\Delta m^2_{21}\) y \(\theta\) y dos experimentales \(E\) y \(L\). Para observar la oscilación, dado un \(\Delta m^2_{12}\) y una energía \(E\) debemos colocar el detector a una distancia \(L\) adecuada.
Consideremos el caso de \(\Delta m^2 = 2 \times 10^{-3} \; \mathrm{eV}^2\) y \(\theta = 47^o\)
Vamos a calcular la probabilidad de oscilación \(P_{\alpha\beta}(L)\)
Cuestion: ¿A qué distancia deberíamos colocar el detector para observar la oscilación máxima?
theta = np.pi * 47/180. # rad
ls = np.linspace(0, 2000, 100) # km
ene = 1. # GeV
delta_m2 = 0.0025 # eV^2
posc = lambda d: np.sin(2*theta)**2 * np.sin(1.27 * delta_m2 * d / ene)**2
plt.plot(ls, posc(ls))
plt.grid(); plt.xlabel(r'$L$ (km)'); plt.ylabel(r'$P_{\alpha\beta}(L)$'); plt.ylim((0, 1.));

3.6.4. Oscilaciones en tres familias#
Como existen tres neutrinos hay dos diferencias al cuadrado de sus masas, que controlan las fases de oscilación de los neutrinos solares, \(\Delta m^2_{sol}\) (por los neutrinos solares) y de \(\Delta m^2_{atm}\) (por los atmosféricos), cuyos valores son [PDG]:
Notar que los neutrinos son quasi-degenerados en masa.
La relación entre los estados de sabor \(\nu_\alpha\) con \(\alpha = e, \mu, \tau\) con los estados de masas \(\nu_i\) con masas \(m_i\) donde \(i = 1, 2, 3\), viene dada por una matriz unitaria \(U_{PMNS}\), conocida como PMNS (Pontecorvo-Maki-Nakagawa-Sakata)
La matiz \(U\) tiene 3 ángulos de mezcla y una fase compleja (de forma similar a la matriz CKM).
Se han medido experimentalmente los tres ángulos [PDG], pero no la fase compleja \(\delta\).
3.6.5. El futuro de las oscilaciones de neutrinos#
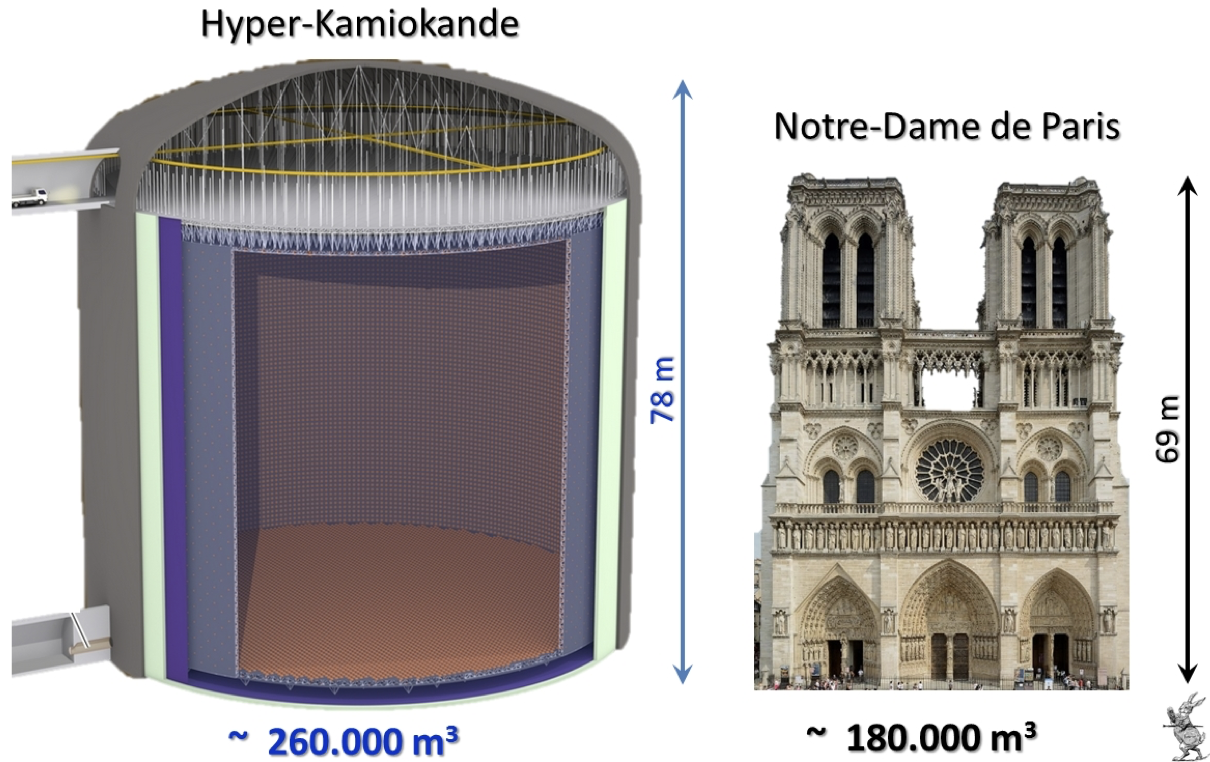
En la próxima década el detector Hyper-Kamiokande, HK en Japón y DUNE en los USA determinarán seguramente la fase \(\delta\) y fijarán nuestra comprensión de las oscilaciones de neutrinos.
HK estudiará las oscilaciones \(\nu_\mu \to \nu_e\) y \(\bar{\nu}_\mu \to \bar{\nu}_e\) con energías de 0.6 GeV y una distancia 295 km, desde su producción en J-Parc hasta su detección en HK en la mina de Kamioka.
Dibujo del detector HK comparado con Notre-Dame de Paris |
[Para esta sección ver y profundizar en AB10.1, AB10.2, AB10.14 y MT13]
3.6.6. Bibliografía#
[AB] Alessandro Bettini, «Introduction to Elementary Particle Physcs», Cambridge U. press. Temas 7 y 10.
[MT] Mark Tomsom, «Modern Particle Physics», Cambridge U. press. Temas 11, 12 y 13.
PDG Particle Data Group.
[WU] C.S. Wu et al, Phys. Rev. D17 2369 (1957)
[MU] M. Bardon, P. Norton, J. Peoples, A. M. Sachs and J. Lee-Franzini, Phys. Rev. Lett. 14, 449 (1965).
[GOL] M. Goldhaber et al, Phys Rev 109 1015 (1958)
[KATRIN] M. Aker et al. (KATRIN Collaboration) Phys. Rev. Lett. 123, 221802 (2019)
[SK] Y. Ashie et al, SK Collaboration, Phys. Rev. D71 112005 (2005)