Fundamentos del Modelo Estándar
Contents
Fundamentos del Modelo Estándar#
Jose A. Hernando
Departamento de Física de Partículas. Universidade de Santiago de Compostela
Diciembre 2023
import time
print(' Last version ', time.asctime() )
Last version Fri Jan 19 17:18:33 2024
# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2
# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.constants as units
Introducción#
El Modelo Estándar define el marco teórico que clasifica la materia y establece las interacciones fundamentales. Su construcción constituye uno de los grandes logros en Física Teórica y está ligada a la evolución de nuestro conocimiento de las interacciones fundamentales a lo largo del siglo XX.
Hay dos pilares básicos que sustentan el modelo: que el lagrangiano sea invariante Lorentz e invariante gauge local. Esta última condición es necesaria para que la teoría sea renormalizables y se puedan calcular observables como la sección eficaz y las anchuras de desintegración sin que aparezcan infinitos en los cálculos.
Las interacciones electromagnéticas y fuertes aparecen en el modelo de manera natural a partir de la invariancia gauge local. Sin embargo, la inclusión de las interacciones débiles requiere cierto encaje, primero porque las interacciones no preservan paridad, y separan los campos en quiralidad a izquierdas y derechas, y segundo, que tras esta separación, para dotar de masa a las partículas es preciso incorporar un mecanismo específico, el mecanismo de Higgs, sin el cual el modelo carece de sentido.
Estas notas presentan una estructura matemática del modelo sin pretender ser exhaustivas. Revisaremos primero los lagrangianos de los campos escalar, espinorial y vectorial. Introduciremos después la invariancia gauge y la derivada covariante en la interaciones electromagnéticas y fuertes. Luego discutiremos la interacción electrodébil, veremos cómo aparecen las corrientes cargadas y neutras, y terminaremos presentando el mecanismo de Higgs con el que dotar de masas a los fermiones y los bosones vectoriales \(W^\pm\) y \(Z^0\).
Simetría gauge#
Vamos a introducir el concepto de simetría gauge utilizando para ello el lagrangiano de Dirac y del campo electromagnético. De tal forma que veremos que podemos dar la interacción electromagnética como una consecuencia de la posibilidad de rotar el campo fermiónico por un fase local, esto es, que el lagrangiano sea invariance gauge bajo el grupo \(U(1)\).
Posteriormente extenderemos el lagrangiano de Dirac para incluir el color de los quaks. En este caso asignaremos los tres colores de un mismo quark a los elementos del triplete del grupo \(SU(3)_C\), donde \(C\) es por color, y veremos que la invariancia gauge de este lagrangiano bajo transformaciones en \(SU(3)_C\) es más rica y compleja que con \(U(1)\).
Recordatorio de los diversos lagrangianos#
Revisión sobre el lagrangiano#
Recordemos que en mecánica clásica definimos el lagrangiano como:
donde \(T\) es la energía cinética, \(V\) el potencial, \(q_i\), con \(i=1, \dots, n\), son las coordenadas generalizadas y \(\dot{q}\) sus derivadas temporales.
y las ecuaciones del movimiento vienen dadas por las escuaciones de Euler-Lagrange:
que provienen de exigir que la acción del sistema, \(S\), sea mínima, siendo:
En el caso de una partícula en un potencial, el lagrangiano es su energía cinética menos su potencial:
Y su ecuación del movimiento:
es la ecuación de Newton.
En teoría clasica de campos definimos un campo \(\phi(x)\) en las coordenadas espacio temporales \(x\) y el lagrangiano del campo como:
donde \(\mathcal{L}(\phi, \partial_\mu \phi)\) es la densidad lagrangiana, o por abuso del lenguaje, el lagrangiano.
La ecuaciones del movimiento vienen dadas por:
que provienen de exigir que la acción es mínima, siendo la acción:
Notar que como la acción no tiene dimensiones y \(\mathrm{d}^4x\) tiene dimensiones de \([E]^{-4}\), el lagrangiano tiene dimensión \([E]^4\). Esto significa que los términos del lagrangiano deben tener dimensión 4 en energía.
Lagrangiano del campo escalar#
Sea \(\phi(x)\) un campo escalar real asociado a partículas de masa \(m\), su lagrangiano viene dado por:
El primer término es la energía cinética y el segundo es el potencial asociado a la masa de la partícula. La masa es entonces la energía mínima para crear la partícula asociada al campo.
La ecuación de movimiento:
es la ecuación de Klein-Gordon
que también podemos escribirla como:
donde hemos definido:
Consideremos ahora un campo escalar complejo, \(\phi\), que está compuesto por dos campos escalares reales e independientes, \(\varphi_1, \varphi_2\):
El lagrangiano del campo complejo corresponde al de los dos campos reales:
Es fácil comprobar que el lagrangiano es invariante respecto a un cambio de fase global
Por último, notar también que las dimensiones del campo, \(\phi\), son de energía, \([E]\).
Lagrangiano de Dirac#
El lagrangiano de un campo de Dirac es:
que corresponde a un término cinético y el del potencial asociado a su masa.
Recordemos que \(\bar{\Psi}(x)\) es el espinor adjunto definido por:
En total hay 8 funciones reales e independientes en \(\Psi\), y que podemos dar con 4 funciones en \(\Psi\) y \(\bar{\Psi}\), de manera similar a considerar como independientes \(\phi^*, \phi\) en el caso de un campo escalar complejo en vez de los dos campos escalares reales \(\varphi_1, \varphi_2\).
Desde el punto de vista de las dimensiones, el espinor, \(\Psi\), tiene dimensión \([E]^{3/2}\), de tal forma que cada término del lagrangiano tenga dimensión \([E]^4\).
La ecuación de Dirac se obtiene a partir de la ecuación del movimiento derivando respecto al espinor adjunto, \(\bar{\Psi}(x)\):
Derivando respecto a \(\Psi(x)\), obtenemos a su vez la ec. de Dirac del espinor adjunto:
Vemos también que el lagrangiano de Dirac es invariante bajo un cambio global de fase:
Donde \(Q\) es una constante, que asociaremos a la carga eléctrica del fermión.
El campo \(\Psi(x)\) es invariante bajo una rotación \(U(\theta)\) del grupo \(U(1)\)
Parece natural que si podemos cambiar la fase del campo de Dirac globalmente, esto es, igual en todos los puntos al mismo tiempo, podamos cambiarla de forma continua en una región o intervalo temporal, eso es cambiarla localmente.
Sin embargo si realizamos un cambio de fase local:
donde ahora \(\theta(x)\) cambia continuamente con \(x\).
Esto es, si exigimos que el lagrangiano sea invariante gauge local respecto a una rotación, \(U(\theta(x))\) del grupo \(U(1)\)
obtenemos que el lagrangiano del campo transformado es:
En el lagrangiano aparece el término:
que no preserva la invariancia gauge.
Podemos interpretar ese término como el acoplo de la corriente:
con un campo vectorial, \(-\partial_\mu \theta(x)\).
El campo es vectorial porque proviene de una derivada covariante, y se comporta por lo tanto como un vector.
Lagrangiano del campo electromagnético#
Sea ahora \(A^\mu(x)\) el campo vectorial del electromagnetismo:
donde \(\phi(x)\) es el potencial eléctrico y \({\bf A(x)}\) el potencial vector magnético.
Notar que se trata de 4 funciones reales.
[TODO] Ecuaciones de Maxwell
Definimos el campo tensor de fuerza, \(F^{\mu\nu}\), como:
Lo que nos permite dar las ecuaciones de Maxwell en ausencia de cargas y corrientes, como:
Estas ecuaciones provienen del lagrangiano:
Notar que las dimensiones del campo \(A_\mu\) son de energía \([E]\).
Podemos explicitar las ecuaciones de Maxwell en función de \(A_\mu\):
que podemos comprobar facilmente que es invariante bajo la transformación:
siendo \(\theta(x)\) una transformación continua en \(x\).
Esto es, hay un conjunto de campos que representan la misma física. La diferencia entre ellos es la derivada de una función continua \(\theta(x)\).
Esta equivalencia de campos la llamamos invariancia gauge.
Podemos utilizar esta invariancia par escoger una gauge determinada, e imponer, sin pérdida de generalidad, que:
A esta gauge la llamamos de Lorenz (¡no Lorentz!).
Con lo que las ecuaciones del movimiento quedan:
Esto es las cuatro componentes \(A^\mu\) cumplen la ecuación de Klein-Gordon para una partícula sin masa. De ahí que el fotón no tenga masa.
Las ecuaciones del campo y la condición de la gauge de Lorenz aún admiten una transformación más del tipo \(A^\mu - \partial^\mu \theta\) que las deja invariantes, siempre que se cumpla la condición adicional:
Es fácil comprobar que un nuevo campo con esa condición, cumpliría también \(\partial_\mu A^\mu = 0, \;\; \square A^\mu = 0\).
Asi de los cuatro grados de libertad iniciales del fotón, dadas las dos condiciones, solo quedan dos grados de libertad, que corresponden a las dos polarizaciones del fotón.
Sea ahora la corriente electromagnética \(j^\mu(x)\)
donde \(\rho(x)\) es la densidad y \({\bf j}(x)\) la corriente espacial de probabilidad y \(Q\) la carga eléctrica.
Las ecuaciones de Maxwell, del movimiento, son ahora:
La corriente es una corriente conservada. Dado que \(F^{\mu\nu}\) es un tensor antisimétrico se cumple:
Las ecuaciones de Maxwell en presencia de carga y corrientes se obtienen de incluir en el lagrangiano un término adicional que acopla el fotón con la corriente:
Y finalmente para representar un fotón masivo, con masa, \(m\), introducimos un término de masa en el lagrangiano:
que se conoce como lagrangiano de Proca.
Que nos daría como ecuación del movimiento, en ausencia de cargas:
Que si contraemos con \(\partial_\nu\) nos queda:
Esto es, se cumple automáticamente, si necesidad de seleccionarla,
la condición de la gauge de Lorenz.
La ecuación del movimiento podemos reescribirla entonces como:
Ahora las cuatro componentes de \(A^\mu\) cumplen la ecuación de Klein-Gordon para una partícula de masa \(m\).
Aunque la condición de la gauge de Lorenz se cumple automáticamente, aún podemos no obstante imponer la condición extra:
Como en este caso solo hay una condición sobre las cuatro componentes de \(A^\mu\), los grados de libertad del campo vectorial son tres, que corresponden a tres polaridades.
No obstante un campo vectorial con masa no preserva la invariancia gauge, ya que:
por eso decimos que los terminos de masa de los bosones vectoriales rompen la simetría gauge local.
Recapitulación#
La siguiente tabla muestra las ecuaciones del movimiento y los lagrangianos de los campos escalar complejo, de Dirac y vectorial.
—– Tipo —– |
——— Escalar Complejo ———- |
———- Espinor ———— |
—— Bosón vectorial ———- |
Klein-Gordon |
Dirac |
Maxwell |
|
Ecuación |
\((\partial^\mu\partial_\mu + m^2) \, \phi = 0\) |
\((i\gamma^\mu \partial_\mu - m) \, \Psi = 0\) |
\(\partial_\mu F^{\mu\nu} = 0\) |
Lagrangiano |
\((\partial_\mu \phi)^* (\partial^\mu \phi) - m^2 \phi^* \phi\) |
\(i\bar{\Psi}\gamma^\mu \partial_\mu \Psi - m \bar{\Psi}\Psi\) |
\(-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}\) |
Donde:
Invariancia gauge#
Electromagnetismo. Derivada Covariante.#
Hemos visto por un lado que exigir la invariancia del lagrangiano con el cambio de fase local del campo de Dirac, implicaba la presencia de un término de interacción de la corriente electromagnética con un campo vectorial; y por otro lado que ese mismo término puede absorberse en el lagrangiano del campo vectorial electromagnético.
Parece natural que unifiquemos entonces ambos en un solo lagrangiano que describa la interacciones electromagnéticas de un fermión de carga \(Q\) y que además preserve la invariance gauge local del fermión:
donde la corriente eléctrica viene dada:
\(Q\) es la carga eléctrica, por ejemplo para el electrón \(Q = -e\).
Que podemos escribir de forma más compacta si introducimos la derivada covariante generalizada:
Como:
Podemos comprobar que este lagrangiano es ahora invariante bajo la tranformación gauge local de \(U(1)\) del campo del fermión, \(\Psi(x)\), si el campo vectorial, \(A^\mu(x)\), cambia de forma acorde:
Es inmediato verificar que el término de masa y el cinético del campo vectorial son invariantes bajo esta transformación.
Para que el término cinético del fermión sea invariante debe cumplir:
donde:
Comprobémoslo:
El campo vectorial de forma genérica debe transformar como:
En este caso con \(U(\theta) = e^{iQ\theta(x)}\), tenemos:
Podemos concluir entonces, que si exigimos que el lagrangiano de Dirac sea invariante respecto a un cambio de fase local del campo \(\Psi\), aparece de forma natural la interacción electromagnética entre la carga eléctrica asociada al fermión y el campo vectorial del fotón.
Decimos que el lagrangiano en invariante gauge bajo al grupo \(U(1)_Q\), donde \(Q\) es por carga.
También vemos que cada fermión puede tener su propia carga eléctrica asociada, \(Q\).
Invariance gauge bajo color#
Sabemos experimentalmente que existen 6 quarks, \(u, d, s, c, b, t\), cada uno de ellos en tres colores: rojo, azúl y verde.
Vamos a extender el campo de Dirac para incluir el color de los quarks. Lo haremos asignando cada color a un elemento del triplete del grupo \(SU(3)_C\), donde \(C\) es por color, y exigiendo de nuevo que el lagrangiano sea invariante bajo rotaciones locales en el espacio interno del color, en \(SU(3)_C\).
Veremos que este caso es más complejo que el del electromagnetismo, dado que los generadores de las rotaciones no conmutan, esto es, se trata de un grupo no abeliano.
El ejemplo del \(SU(3)\) se puede extender a otros grupos \(SU(N)\), en particular al \(SU(2)\) como veremos más adelante en la sección de las interacciones electrodébiles.
Sabemos que los quarks vienen en tres colores, rojo, azul y verde, podemos asignar el campo de cada color de un quark, \(q^\alpha\), con los elementos de un triplete de \(SU(3)\), con \(\alpha = r, b, g\).
así:
Estamos usando una notación vectorial donde cada elemento corresponde al espinor de Dirac asociado al color del quark.
El lagrangiano de Dirac para un quark con tres colores podemos darlo como:
donde:
Se puede comprobar fácilmente que este lagrangiano es invariante bajo la rotación global en \(SU(3)_C\).
Donde \(U({\bf \theta})\) es la matriz de rotación, que es unitaria, \(U^\dagger U = I\), y \(g_S\) es una constante, que llamaremos constante de acoplo fuerte.
Esto es rotamos globalmente por los ángulos \(\theta_a\) sobre cada generador, \(T_a\), de \(SU(3)\).
El grupo \(SU(3)\) tiene 8 generadores, \(a = 1, \dots, 8\).
Los generadores podemos expresarlos en función de las matrices de Geldmann:
que cumplen las siguientes reglas de conmutación:
donde \(f^{abc}\) son las constantes de estructura del grupo, que son reales y totalmente antisimétricas.
Lo que nos dice que los generadores no conmutan, así que tendremos que tener cuidado a la hora de expandir el exponente, \(e^{i g_S \theta^a T_a}\) para calcular la matriz de rotación, \(U({\bf \theta})\).
Notar que la discusión sería similar si hubiésemos usando el grupo \(SU(2)\), en ese caso el número de generadores sería tres.
donde \(\sigma_i\) son las matrices de Pauli, con \(i = 1, 2, 3\).
La estructura del grupo \(SU(2)\) es bien conocida:
que se sigue inmediatamente de las propiedades de las matrices de Pauli.
Exigimos ahora que el lagrangiano de Dirac del quark de colores sea invariante bajo rotaciones locales en el espacio interno de \(SU(3)_C\), esto es, bajo:
Para ello, de forma similar a como hicimos en el caso del electromagnetismo, introduciremos la derivada convariante:
Donde \(g_S\) será la constante fuerte, y \(G^a_\mu(x)\) los 8 campos vectoriales asociados a cada generador. Notar que el índice \(a\) esta contraido, luego significa un sumatorio en los 8 términos. Físicamente cada campo vectorial \(G_\mu^a(x)\) corresponde a cada uno de los 8 tipos de gluones de cromodinámica cuántica.
Al igual que hicimos en el electromagnetismo, las transformaciones de los campos, \(G^a_\mu(x)\) serán tales que la derivada covariante se transforme igual que \(q\), esto es:
para preservar la invariancia gauge local.
Las condiciones sobre la derivada covariante y sobre el campo transformado son iguales que para el caso del electromanetismo.
El campo transformado será:
Consideremos una transformación infinitesimal:
Por lo tanto el término:
Mientras que el término:
Luego, componente a componente:
Vemos pues que las transformación de los campos de gluones es compleja e involucra todos los gluones.
También vemos que nos aparece la constante \(g_S\) en la transformación. Esto hace que el acoplo fuerte de todos los quarks sea el mismo, independiente de su sabor, mientras que para cada fermión podíamos asociarle a cada uno una carga eléctrica.
[EXT] comentario sobre la parte cinética del lagrangiano
Finalmente si consideramos los seis sabores de quarks, \(f = u, d, c, s, b, t\), el lagrangiano de QCD es:
Unificación electrodébil#
Las interacciones débiles, en concreto las cargadas, violan paridad, y ese implica que tratan de forma diferente las componentes de quiralidad a izquierdas y derechas de un campo fermiónico.
Sabemos también que en la corrientes cargadas, mediadas por los bosones vectoriales, \(W^\pm\), solo interviene la quiralidad a izquierdas de los fermiones. Sin embargo en la corrientes neutras, mediadas por el bosón vectorial \(Z^0\), intervienen ambas quiralidades y con pesos diferentes.
Parece natural entonces que para dar las interaciones débiles debemos tratar las dos quiralidades por separado.
Sabemos que \(\Psi\) se divide en sus dos componentes de quiralidad, via los proyectores a izquierdas y derechas, \(P_L, \, P_R\):
También sabemos que la corriente, la forma vectorial, se descompone en dos corrientes, una a izquierdas y otra derechas, pero que el término escalar, el asociado a la masa, mezcla las dos quiralidades, esto es:
Vimos también que la quiralidad se intercambiaba bajo la inversión por paridad:
Para construir el lagrangiano de las interacciones débiles, vamos a separar entonces las dos componentes de quiralidad.
El lagrangiando de Dirac nos queda:
Pero para separar completamente las dos quiralidades ¡estamos obligados a que el fermión no tenga masa!
Admitamos por ahora fermiones sin masa e ignoremos por el momento (hasta más adelante) el hecho de que los fermiones sí tienen masas.
En ese caso, tenemos dos campos independientes:
Sabemos también que en las desintegración débiles cargadas siempre aparecen los fermiones en parejas, por ejemplo el leptón cargado, el electrón, con el neutrino de su sabor, el \(\nu_e\).
Para acomodar este hecho, podemos situar los campos a izquierdas del leptón cargado y su neutrino en un duplete que llamaremos de quiralidad a izquierdas:
donde para facilitar la lectura vamos a introducir la notación:
esto es, el espinor a izquierdas del neutrino es \(\nu_{eL}\) y el del electrón, \(e_L\)
Estamos pues asociando los espinores a izquierdas de las parejas en un duplete que llamamos de isoespín débil, del grupo \(SU(2)_L\) donde \(L\) es por la quiralidad a izquierdas.
En este caso, el \(\nu_{eL}\) tiene tercera componente de isoespín débil \(+1/2\) y el \(e_L\) tiene \(-1/2\).
Al haber colocado los campos de las parejas en el duplete, podemos entender la acción de un campo \(W^\pm\) como subir o bajar los elementos del duplete.
Notar que esta agrupación es similar a cuando introdujimos la notación \(q\) como un triplete donde situamos en sus elementos los campos asociadas a los colores de cada sabor de quark.
Sabemos no obstante que en las corrientes neutras participan los espinores a derechas luego es preciso incluirlos.
La componente a derechas la situamos en un singlete de isoespín débil.
donde \(e_R\) es el espinor a derechas del electrón.
En este caso, el Modelo Estándar predice que el neutrino no tiene componente a derechas, no existe \(\nu_R\).
La primera familia de leptones es un duplete a inzquierdad y un singlete a derechas:
Y de forma similar agruparíamos las otras dos familias leptónicas
Para los quarks, la situación es similar, los espinores a izquierdas forman un duplete y los de derechas un singlete de isoespín.
El espinor del quark con mayor carga del duplete se situa en el elemento de arriba an el duplete, esto es, tiene tercera componente de isoespín débil, \(I_{W3} =1/2\) mientras que el de menos carga aparece abajo en el duplete, con \(I_{W3} = -1/2\). La diferencia de carga entre los dos es 1.
Finalmente, los dos quarks de la pareja tiene ambos singletes a derechas.
Asi pues, los fermiones se agrupan en dupletes de quiralidad a izquierdas y singletes a derechas.
Para la primera familia de fermiones:
Nota: No confundir el espinor \(u(p)\), con la notación \(u_L\), este último significa el espinor a izquierdas del quark \(u\).
También hay que tener cuidado con los espinores conjugados, \(\bar{\nu}_L\) corresponde al conjugado del espinor a izquierdas del neutrino, y no a la componente a izquierdas del anti-neutrino (¡que no existe!).
La siguiente tabla muestra el isoespín débil y su tercera componentes para los leptones de la primera familia.
En la primera familia, la electrónica:
\(\nu_{eL}\) |
\(e_L\) |
\(e_R\) |
|
\(I_{W}\) |
+1/2 |
+1/2 |
0 |
\(I_{W3}\) |
+1/2 |
-1/2 |
0 |
La tabla para el resto de familias leptónicas sería similar.
Y la siguiente tabla muestra el isoespín y tercera componente para la primera familia de quarks:
\(u_L\) |
\(d_L\) |
\(u_R\) |
\(d_R\) |
|
\(I_{W}\) |
+1/2 |
1/2 |
0 |
0 |
\(I_{W3}\) |
+1/2 |
-1/2 |
0 |
0 |
Y de forma similar obtendríamos la tabla para el resto de familias de quarks.
Simetría gauge local \(SU(2)\)#
Separemos ahora el lagrangiano de Dirac en sus componentes del doblete de izquierdas y el singlete a derechas.
Indicamos aquí solamente el de la primera familia de leptones, pero sería idéntico para los quarks y para el resto de familias de fermiones.
Podemos comprobar facilmente que el lagrangiano es invariante bajo una rotación global del duplete en el espacio de isospín débil.
Es este caso, el espacio interno \(SU(2)_L\) tiene tres generadores, \(\tau_i\), que están relacionados con la matrices de Pauli,
con \(i = 1, 2, 3\).
Notar que la rotación tienen tres fases, \(\theta_i\), asociadas a cada generadores.
Y \(g_W\) es una constante real, la constante de acoplo débil.
Exigimos ahora que lagrangiano sea invariante bajo una transformación gauge local del espacio interno del isospín débil, \(SU(2)_L\), donde \(L\) indica que solo afecta a los estados de quiralidad a izquierdas.
El lagrangiano sería invariante bajo la rotación continua local:
Esto es, si modificamos las fases del espacio del isoespín de forma continua en el espacio tiempo.
El lagrangiano quedará invariante.
Lo que a su vez implica que para cada generador \(\tau_i\) existe un campo vectorial \(W^i_\mu(x)\) al que se acoplan las corrientes de los miembros del duplete.
Introducimos la derivada covariante:
Podemos dar explícitamente la expresión:
simplemente haciendo uso de las matrices de Pauli.
Podemos también reescribir:
donde recordemos:
Si definimos los campos:
notar que:
Tenemos entonces que:
Los términos asociados que aparecen en el lagrangiano son:
Donde definimos las corrientes cargadas como:
con una constante de acoplo \(g_W/\sqrt{2}\)
Si desarrollamos explícitamente la corriente podemos comprobar que efectivamente obtenemos la corriente esperada:
Así pues, hemos conseguido acomodar las corrientes cargadas débiles y nos han aparecido los campos vectoriales \(W^{\pm}\)
Sin embargo el término de interacción:
¡no corresponde a las corrientes neutras!, porque en las corrientes neutras intervienen también los espinores a derechas del electrón, \(e_R\).
Para implementar las interacciones neutras, vamos a extender la simetría del lagrangiano exigiendo que sea también invariante gauge local también respecto a una fase, esto es respecto al grupo, \(U(1)_Y\) donde \(Y\) es por hypercarga.
Así introducimos la derivada covariante extendida como:
siendo \(B_\mu\) es el campo vectorial asociado y \(g_Y\) la constante de acoplo de la hypercarga.
Dado que se trata de una simetría de tipo \(U(1)\) cada uno de los campos del lagrangiano, en este caso \(L, e_R\), tienen asociados un valor de hypercarga, \(Y, Y_R\), respectivamente.
Notar que si hubiésemos considerado que las partículas tienen masa, estos campos ya no sería independientes y no podríamos asociarles un valor distinto de hypercarga.
Notar también que la hypercarga no puede ser la carga eléctrica, porque sabemos que los elementos del duplete tiene un mismo valor de hypercarga \(Y\) mientras que el neutrino no tiene carga eléctrica y el electrón tiene carga -1 y ambos comparten duplete.
Vamos a intentar asociar los términos que nos aparecen en el lagrangiano:
con la interacción débil neutra y a la interacción eléctromagnética:
Donde, \(Z_\mu, A_\mu\) son los campos asociados al bosón \(Z^0\) y al fotón; y \(j^\mu_Z\) y \(j^\mu_{Q}\) las corrientes neutras y electromagnéticas respectivamente.
Por la expresión anterior, podemos considerar que los campos físicos \(A_\mu, \, Z_\mu\) son una combinación lineal de los campos subyacentes, \(W^3_\mu, \, B_\mu\).
La relación entre ambos vendría dada por la matriz de mezcla:
donde \(\theta_W\) se denomina ángulo de Weinberg.
Para facilitar la lectura definimos:
Si reescribimos los interacciones fundamentales en función de las físicas:
En el primer sumando, el término que se acopla al fotón, \(A_\mu\), debe corresponderse con la corriente electromagnética:
Y el segundo, con las corrientes neutras:
Corrientes electromagnéticas#
Si desarrollamos la expresión de la corriente electromagnética para el caso de las primera familia de los leptones obtenemos:
Esto es:
El neutrino no tiene corriente eléctrica, luego debe cumplirse que:
mientras que para electrón, las corrientes a izquierdas y derechas deben tener un mismo factor que es su carga eléctrica \(Q = -e\).
Ambas condiciones se cumplen, si:
esto es:
El ángulo de Weinberger puede expresarse como:
y además:
En general vemos que para cada campo fermiónico a derechas se cumplirá:
En el caso del \(\nu_e\), de forma natural \(Y_R = 0\).
Mientras que la hypercarga tiene un valor tal que nos permite obtener la carga de los elementos del duplete:
donde \(I_{W3}\) es la tercera componente de isospín débil.
Esto es el elemento de arriba del duplete tiene siempre una carga eléctrica +1 respecto a la de abajo.
La siguiente tabla muestra los valores de hypercargas para los leptones y los quarks a izquierdas:
\(L_e\) |
\(Q_u\) |
|
|---|---|---|
\(Y\) |
-1/2 |
1/6 |
Y para los componentes a derechas:
\(e_R\) |
\(u_R\) |
\(d_R\) |
|
|---|---|---|---|
\(Y_R\) |
-1 |
2/3 |
-1/3 |
Hemos recuperado pues la descripción de las interacciones electromagnéticas.
Corrientes neutras#
Si regresamos a la corrientes débiles neutras nos encontramos con:
Si explicitamos la corriente para el caso de la primera familia de leptones:
Introduciendo el valor de \(e = s_W g_W\):
Sin definimos:
Obtenemos:
El acoplo con las componentes a izquierdas y derechas del neutrino es:
Mientras que para el electrón, el acoplo a izquierdas y derechas vale:
De forma genérica, las corrientes neutras de un fermión con espinor \(u\) son:
donde \(Q_f\) la carga eléctrica del fermión en unidades de electrón, por ejemplo para el \(e\), \(Q_f = -1\), y \(I_{W3}\) es la tercera componente de isoespín débil.
Que podemos dar de forma compacta:
siendo \(c_R, \, c_L\) los factores a izquierdas y derechas:
La siguiente tabla da los distintos acoplos a izquierdas y derechas de la corriente neutras para la primera familia de fermiones:
—– \(c_R\) —- |
—– \(c_L\) —- |
|
\(\nu_e\) |
0 |
\(\frac{1}{2}\) |
\(e\) |
\(s^2_W\) |
\(-\frac{1}{2} + s^2_W\) |
\(u\) |
\(-\frac{2}{3}s^2_W\) |
\(\frac{1}{2} - \frac{2}{3}s^2_W\) |
\(d\) |
\(\frac{1}{3}s^2_W\) |
\(-\frac{1}{2} + \frac{1}{3} s^2_W\) |
Y de forma similar la obtendríamos para el resto de familias.
Resumen#
Hemos construido un lagrangiano que es invariante gauge local respecto a los grupos \(SU(2)_L\times U(1)_Y\), de tal forma que nos acomoda las corrientes neutras, débiles y electromagnéticas.
Hemos agrupado los campos de los fermiones en dupletes a izquierdas y singletes a derechas, lo que impone que los fermiones no tengan masa.
Hemos obtenido cuatro bosones vectoriales, dos de ellos son los bosones \(W^\pm\), que median entre las corrientes cargadas, y otros dos son los bosones \(A, Z^0\), que a su vez las corrientes electromagnéticas y neutras, respectivamente, y que son combinaciones lineales de los bosones subyacentes \(B, W^3\) a través de un ángulo de mezcla, \(s_W\).
El modelo tiene dos parámetros \(g_Y, g_W\) que se corresponden con los parámetros físicos, \(e, s_W\), y que fijan los acoplos de las tres corrientes: \(e, g_W, g_Z\).
Sin embargo, hemos pagado un precio elevado: los fermiones y los bosones vectoriales no tienen masa.
En la siguiente seccion vamos a tratar cómo resolver este problema.
El mecanismo de Higgs#
Brout, Englert and Higgs desarrollaron en los 60 un mecanismo que permite dotar de masa a los bosones vectoriales y también a los fermiones, y que preserva la invariancia gauge del lagrangiano, fundamental para que la teoría sea renormalizable.
Este mecanismo introduce un campo escalar cuya partícula asociada es el bosón de Higgs. Pero no fue hasta la segunda década del siglo XXI cuando se descubrió el bosón de Higgs en los experimentos ATLAS y CMS.
Inspeccionemos primero el término del lagrangiano asociado a la masa de los fermiones
Vamos a intentar substituir \(m\) por el acoplo a un campo escalar, \(\phi\), que la reemplace. Recordemos que \(m\) y \(\phi\) tienen ambos dimensión de energía, \([E]\).
Consideremos una interacción de los fermiones con un campo escalar complejo, \(\phi\), con una constante de acoplo \(\lambda\), que denominamos acoplo de Yukawa. Para ello introduciremos en el lagrangiano un término:
Y consideremos además que el campo \(\phi\) tiene un valor no nulo en el estado de mínima energía, esto es, en vacío, \(\phi_0\):
El término que hemos introducido da lugar a dos, que corresponden a un término de masa y a otro de interacción con un campo \(H(x)\)
Donde podemos asociar la masa a:
Pero ¿cómo un campo escalar obtiene ese valor en vacío, \(\phi_0\)?
Examinemos primero el lagrangiano de un campo escalar complejo, \(\phi(x)\):
El término de masas podemos entenderlo como un potencial parabólico en \(\phi^* \phi\).
Consideremos la primera extensión de ese potencial:
El potencial debe estar acotado inferiormente para que su energía mínima tenga un límite inferior, esto implica que \(\lambda \gt 0\), ya que el término cuadrático es el dominante.
[TODO] Mostrar la dependencia
En el caso de que \(\lambda = 0\), \(\mu = m \), corresponde a la masa, y recuperamos la situación de partida.
Para \(\lambda \gt 0\) tenemos dos posibilididades:
que \(\mu^2 \gt 0\), en ese caso, el potencial tienen un mínimo trivial en \(\phi_0 = 0\).
que \(\mu^2 \lt 0\), y en este caso, tenemos un número infinitos de mínimos, que cumplen:
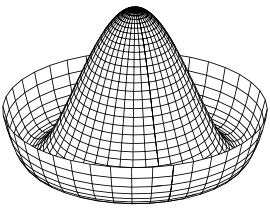
El potencial con \(\mu^2 <0\) y \(\lambda >0\) se conoce como el potencial del sombrero mexicano:
|
potencial del campo complejo de Higgs \(V(\phi)\) [Wikipedia] |
Donde los ejes de la figuran son la componente real e imaginaria de \(\phi\).
Así pues podemos conseguir un campo escalar complejo con un valor esperado en el vacío ,\(\phi_0\), si le dotamos de un potencial de sombrero mexicano con \(\mu^2 \lt 0\) y \(\lambda \gt 0\).
En la literatura es habitual tomar como notación \(\phi_0 = v/\sqrt{2}\), donde \(v\) se denomina el valor esperado del campo en el vacío.
Al cuantificar los campos, el campo tiene como valor esperado en vacío:
Cuestión Verificar que el valor mínimo del potencial es:
Bosón de Goldstone#
Resescribimos ahora nuestro campo complejo, \(\phi(x)\), con dos campos reales, \(\varphi_1(x), \varphi_2(x)\), respecto al valor del campo que corresponde al mínimo del potencial que tiene solo componente real.
Esto es seleccionamos un valor del campo específico de todos los posibles mínimos respecto al que desarrollar el campo. Esta elección rompe la simetría de los valores del campo donde el potencial es mínimo. De ahí que llamemos está elección rotura espontánea de simetría.
Ciertamente la física no puede quedar afectada por la elección de este mínimo.
Así tenemos:
y
El potencial, al tomar \(\mu^2 = -\lambda v\), es:
Notar que en el desarrollo del potencial los términos solo en \(\varphi_1\) y solo en \((\varphi^2_1 + \varphi^2_2)\) se anulan.
El potencial queda:
donde el primer término es el valor mínimo del potencial \(V(\phi)\), el segundo es el término de masas del campo \(\varphi_1\), con masa:
y los dos últimos términos corresponde a la interacción entre los campos, \(\varphi_1, \varphi_2\).
Luego de los dos campos reales, uno, el asociado a la componente real, adquiere masa, esto es requiere un mínimo de energía para crear su partícula asociada, dicha masa corresponde con la curvatura alrededor de la base del sombrero, y el segundo campo, el asociado a la componente compleja, no tiene masa, su potencial es nulo y se corresponde con el hecho de que el potencial no cambia al desplazarse a lo largo de la base del sombrero.
Este segundo campo se le conoce como bosón de Goldstone, y refleja el hecho de que el mínimo del potencial tiene una simetría.
[TODO] dibujo indicativo
Consideremos ahora que el lagrangiano del campo escalar complejo, \(\phi(x)\), con el potencial del sombrero mexicano:
con
E impongamos que el lagrangiano respecta la simetría gauge local respecto a un cambio de fase local en \(\phi(x)\),
Sabemos que tenemos que extender el lagrangiano para incluir el término cinético de un campo vectorial, \(A_\mu(x)\), y sustituir la derivada por la derivada convariante.
Podemos dar el campo de forma genérica como:
a partir de su componente real \(\varphi_1(x)\) y una rotación \(\theta(x)\).
Si escogemos una gauge tal que \(\theta(x) = 0\), que llamamos gauge unitaria, y desarrollamos el vampo respecto a su valor en el mínimo del potencial, obtenemos:
donde \(H(x)\) es un campo escalar real.
La derivada covariante queda:
El desarrollo del término cinético del campo escalar nos queda:
Esto es:
Donde el primer término es el término cinético del campo \(H\).
El segundo término es un término de masa del bosón \(A^\mu\), con:
Y los dos otros términos son la interacción entre el campo \(H\) y el bosón \(A_\mu\), con vértices de tres y cuatro segmentos, respectivamente.
Luego hemos dotado de masa al bosón \(A_\mu\) pero además hemos introducido un campo escalar, de Higgs, con una masa, y que tiene interacciones no triviales con el bosón \(A_\mu\).
Si atendemos a los grados de libertad, el campo \(\varphi_2\) ha desaparecido y se ha «convertido» en un grado de libertad más del campo \(A_\mu\), que sin masa tiene dos polarizaciones, y con masa, tres.
A veces en la literatura se dice que el campo \(A_\mu\) se ha comido el bosón de Goldstone \(\varphi_2\).
Masa de los bosones vectoriales#
El caso anterior es un caso académico, donde hemos usando la simetría gauge U(1) del lagrangiano del campo escalar para dotar de masa a un hipotético bosón vectorial.
Pero el problema real es cómo dotar de masa a los bosones vectoriales débiles, \(W^\pm, Z^0\).
En este caso necesitaremos tres bosones de Goldstone para generar la masa de los tres bosones vectoriales, lo que nos lleva a que el campo de Higgs debe tener al menos 4 componentes reales.
Consideremos que el campo de Higgs es un duplete de campos escalares complejos:
donde \(\phi^+(x)\) es un campo escalar complejo con una carga eléctrica asociada \(+1\), mientras que \(\phi^0(x)\) es también un campo escalar complejo con carga eléctrica nula.
El porqué es un duplete quedará más claro cuando en la siguiente sección dotemos de masa a las fermiones.
Consideremos que el lagrangiano de este campo es:
donde:
con \(\mu^2<0, \lambda \gt0\), siendo \(g_W, \, g_Y\) la intensidad de los acoplos débil y de hypercarga respectivamente, y \(\tau_i = \frac{\sigma_i}{2}\) los generadores del grupo \(SU(2)\).
Este Lagrangiano es por lo tanto invariante gauge bajo el grupo \(SU(2)_L \times U(1)_Y\), y el campo está sometido a potencial del tipo sombrero mexicano.
La hypercarga del duplete es \(Y = 1/2\) de tal forma que la carga eléctrica del elemento de abajo del duplete de Higgs, \(\Phi\), sea nula:
El mínimo de potencial es de nuevo \(v/\sqrt{2}\)
Rompemos la simetría del valor del campo en el mínimo de potencial y desarrollamos el campo de forma genérica a partir de valor en el mínimo que tiene solo componente real en el elemento de abajo del duplete:
donde \(H(x)\) es un campo escalar real, y \(\theta^i(x)\) son 3 funciones reales.
Podemos usar la invariancia gauge para seleccionar una gauge específica donde \(\theta^i(x) = 0\), que llamamos unitaria.
Notar que esta gauge nos asegura que el campo que sobrevive esté asociado con el campo físico que llamamos de Higgs.
La derivada covariante:
donde \(Y= \frac{1}{2}\).
Si la expresamos con el campo desarrollado a partir del valor en el vacío y en la gauge unitaria.
Podemos reescribir el término donde aparecen los campos \(W^3_\mu, B_\mu\) con los de los bosones físicos, \(A_\mu, Z_\mu\):
donde hemos usando que \(g_Y = g_W \tan \theta_W, g_Z = g_W/c_W\).
O equivalentemente, como el fotón no tiene masa, sabemos que para que se anule su factor en la expresión anterior debe cumplirse:
esto es, debe cumplirse la siguiente una relación entre las intensidades de acoplo:
que es relación que nos había aparecido antes, al desarrollar la unificación electrodébil.
Así:
Teniendo en cuenta que \((W^+)^\dagger = W^-\), el término cinético del lagrangiano en la gauge unitaria queda:
Luego hemos obtenido un término de masas para los bosones vectoriales \(W^\pm, Z^0\), que es:
Lo que establece la misma relación entre las masas que entre los acoplos:
Notar que dadas las constantes de acoplo débil, que fijan las interacciones débiles con los fermiones, junto con \(v\), también fijan la masa de los bosones vectoriales.
Esto es, el modelo de Higgs no introduce parámetros adicionales asociados con la masa de los bosones \(W^\pm, Z^0\), y ésta esta fijada por los parámetros \(g_Y, g_W, v\).
Pero notar también que además de los términos de masa de los bosones, nos han aparecido en el lagrangiano una serie de términos que corresponden a las interacciónes de Higgs con los bosones vectorials \(W^\pm, Z^0\).
La física que se deduce de estas interacciones es muy rica y compleja, que no vemos en estas notas.
Pero si havemos notar que intensidad de la interacción de los campos vectoriales con el Higgs:
es proporcional a su masa de los bosones.
Recordemos ahora que en los diagramas de Feynman de las corrientes débiles nos aparece el factor (al cuadrado) asociado a los vértices y el propagador, que si el cuadrimomento transferido es pequeño comparada con la masa de los bosones podemos aproximar por:
Y sabemos que este factor está asociado a la constante de Fermi:
Esto es el valor esperado en el vacío, \(v\), está asociado con la constante de Fermi, \(G_F\).
Asi pues la unificación electrodébil tiene cuatro parámetros físicos, dos asociados al bosón de Higgs, \(G_F, m_H\), la constante de acoplo de Fermi y la masa del Higgs, y \(e, s_W\), la carga eléctrica del electrón y el seno del ángulo de Weinberger.
Desde punto de vista teórico los parámetros son \(v, \lambda, g_Y, g_W\).
Masas de los fermiones#
Para dotar de masa a los fermiones debemos recuperar el término en el lagrangiano que acople el campo a izquierdas con el de derechas a través del campo de Higgs.
Al haber situado los campos a izquierdas en un duplete y los de derechas en un singlete de isospín, debemos establecer un acoplo con el campo de Higgs de tal forma que sea un escalar e invariante Lorentz. Por ello, introducimos los términos:
donde \(\lambda_e\) es una constante de acoplo de Yukawa. El segundo término simplemente es el hermítico conjugado, \(\mathrm{h.c.}\)
Tras la rotura espontánea de simetría el término queda:
Esto es:
Nos aparece un término de masas del electrón:
y un término de interacción del electrón con el campo de Higgs:
La masa del electrón es entonces:
Y la interacción del electrón con el Higgs es proporcional a:
la masa del electrón.
Y obraríamos de forma simular para el resto de familias leptónicas.
En este caso al no existir el campo a derechas del neutrino no podemos dotarle de masa.
Si consideramos ahora la primera familia de los quarks, unos terminos similar a los anteriores nos dotaría de masa al quark \(d\) pero para dotar de masa al quark \(u\) necesitamos introducir términos adicionales.
Para ello definimos primero el conjugado del duplete del campo de Higgs:
que tras la rotura espontánea de simetría y la elección de la gauge unitaria queda:
Si introducimos ahora los términos de interacción de los quarks con el campo de Higgs como:
donde \(\lambda_u, \lambda_d\) son las constante de acoplo de Yukawa del quark \(u, d\) respectivamente.
Notar que ambos términos son escalares respecto al isoespín débil, y nos acoplan los campos a izquierdas y derechas de cada quark.
Tras la rotura espontánea de simetría y en la gauge unitaria obtenemos:
Esto es, los términos de masas para los quarks \(u, d\):
Y los de la iteracción de los quarks con el bosón de Higgs, cuya constante de acoplo de Yukawa:
es proporcional a la masa de quada quark.
Obraríamos de igual forma para el resto de familias de quark.
Notar por lo tanto que para cada fermión cargado introducimos una constante de acoplo de Yukawa. Esto es hay tantos parámetros libres adicionales como masas de los quarks.
Y también que el acoplo con el campo de bosón de Higgs es proporcional a la masa de cada fermión. El bosón de Higgs se acopla con más intensidad con los fermiones más pesados.
En resumen el Higgs se acopla a los fermiones y los bosones vectoriales, \(W^\pm, Z^0\), proporcionalmente a su masa.
Recapitulemos, para dotar de masa a la primera familia de fermiones introducimos los siguientes términos de interacción:
que además de dotar de masa al electrón y a los quarks \(u, d\), fijan las interacciones de los mismos con el bosón de Higgs.
Parámetros del modelo#
Recapitulemos y resumamos los parámetros que aparecen en el Modelo Estándar.
El campo de Higgs introduce dos parámetros, \(v, \lambda\), que experimentalmente están asociados a \(G_F\) y la masa del Higgs \(m_H\)
La interacción electrodébil introduce dos parámetros \(g_W, g_Y\) que experimentalmente están asociados a la carga del electrón, \(e\), (o la constante de estructura fina \(\alpha\)) y el seno del ángulo de Weinberger \(s_W\). Y que, junto con \(v\) (o \(G_F\)), establecen la masa de los bosones vectoriales \(M_W, M_Z\).
La interacción fuerte introduce una constante de acoplo \(g_S\) o experimentalmente la constante \(\alpha_S\).
Finalmente tenemos tantos acoplos de Yukawa como fermiones cargados, esto es, 3 por familia. Para la primera familia, \(\lambda_e, \lambda_u, \lambda_d\), o experimentalmente las masas \(m_e, m_u, m_d\).
No hemos considerano en nuestra discusión la mezcla de sabores de los quarks que nos introduciría 4 parámetros adicionales, asociados a la matriz CKM, tres ángulos de mezcla y una fase compleja.
Si consideramos la masa de los neutrinos y su mezcla el modelo tiene 3 más 4 (o 6) parámetros adicionales, 3 de las masas y 4 de la matriz de mezcla PMNS y dos posibles fases si los neutrinos son de Majorana.
Bibliografía#
[MT] Mark Tomsom, «Modern Particle Physics», Cambridge U. press, Temas 15, 16 y 17.
[AB] Alessandro Bettini, «Introduction to Elementary Particle Physcs», Cambridge U. press, Tema 9.
[TP] Antonio Pich, «The Standard Model of Electroweak Interactions», (2012), arXiv:1201.0537v1
[PK] M. Peskin, Lectures on the Theory of the Weak Interaction, SLAC–PUB–17142, (2017), arXiv:1708.0943v1