Sobre los quarks y los hadrones
Contents
4. Sobre los quarks y los hadrones#
import time
print(' Last version ', time.asctime() )
Last version Wed Oct 15 10:04:04 2025
# general imports
%matplotlib inline
%reload_ext autoreload
%autoreload 2
# numpy and matplotlib
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.constants as units
4.1. Objetivo#
Presentar los principales hadrones y bariones, junto con sus características: confinamiento, hadronización y libertad asintótica.
Mostrar la existencia de los quarks y el color mediante el proceso \(e+e^+ \to q + \bar{q}\)
Analizar las desintegraciones débiles cargadas en hadrones y cómo se produce la mezcla entre las familias de quarks.
Proporcionar unos apuntes sobre QCD.
4.1.1. Introducción#
Los hadrones son las partículas que sienten la interacción fuerte. Están compuestos por quarks y se dividen en:
bariones: combinación de tres quarks, con carga eléctrica entera.
mesones: una combinación de quark-anti-quark, también con carga eléctrica entera.
El protón es el único barión estable, con unva vida media mayor que \(\tau_p \gt 3.6 \, 10^{29}\) y.
Algunos bariones relevantes:
nombre |
quark composition |
\(J^{P}\) |
mass (MeV) |
life-time |
main decays |
|---|---|---|---|---|---|
\(p\) |
(uud) |
\(1/2^+\) |
\(938.27\) |
\(>3.6 \, 10^{29}\) y |
None |
\(n\) |
(udd) |
\(1/2^+\) |
\(939.56\) |
\(874.4\pm0.6\) s |
\(p +e +\bar{\nu}_e\) (100%) |
\(\Delta\) |
(uuu) |
\(3/2^+\) |
\(1232 \pm 2\) |
\(118 \pm 2\) MeV |
\(p + \pi^-, n+ \pi^0\) |
\(\Lambda\) |
(uus) |
\(1/2^+\) |
\(1115.683 \pm 0.006\) |
\(263 \pm2\) ps |
\(p + \pi^0, n+ \pi^+\) |
\(\Sigma^0\) |
(uds) |
\(1/2^+\) |
\(1182.64 \pm 0.02\) |
\(7.4 \pm 0.7 \, 10^{-20}\) s |
\(\Lambda+\gamma\) |
\(\Omega^-\) |
(sss) |
\(3/2^+\) |
\(1672.45 \pm 0.29\) |
\(82.1\pm 1.1\) ps |
\(\Lambda+K^+, ...\) |
donde \(J^P\), indica el spin \(J\), y \(P\) el signo que se introduce en la función de ondas al aplicar el operador paridad.
Algunos mesones relevantes:
nombre |
quark composition |
\(J^{P}\) |
mass (MeV) |
life-time |
main decays |
|---|---|---|---|---|---|
\(\pi^0\) |
\((\bar{u}u, \bar{d}d)\) |
\(0^-\) |
\(134.97\) |
\(8.43\pm0.6 \, 10^{-17}\) s |
\(2\gamma\) (98%) |
\(\pi^\pm\) |
(\(u\bar{d}, \bar{u}d\)) |
\(0^{-}\) |
\(139.57\) |
\(26.033\pm0.05\) ns |
\(\mu + \bar{\nu}_\mu\) (98%) |
\(\rho\) |
(\(u\bar{u}, \bar{d}d\)) |
\(1^-\) |
\(7775.5\pm0.4\) |
\(194.4\pm1\) MeV |
\(2\pi\) |
\(K^\pm\) |
\((\bar{s}u, s\bar{u})\) |
\(0^{-}\) |
\(493.677\pm 0.016\) |
\(12.39\pm0.02\) ns |
\(\mu+ \bar{\nu}_\mu\) (63%), \(\pi^- \pi^0\) (20 %) |
\(K^0_S\) |
\((\bar{s}d, \bar{d}s)\) |
\(0^{-}\) |
\(497.648\pm0.022\) |
\(89.5\pm0.05\) ps |
\(\pi^++\pi^-\) (69%), \(2\pi^0 \) (30%) |
\(K^0_L\) |
\((\bar{s}d, \bar{d}s)\) |
\(0^{-}\) |
\(497.648\pm0.022\) |
\(51.14\pm0.21\) ns |
\(\pi^\pm + e^\pm + \nu_e\) (40%), \(\pi^\pm + \mu^\pm + \bar{\nu}_\mu\) (27%) |
\(\phi\) |
\((s\bar{s})\) |
\(1^-\) |
\(1019.46\pm0.019\) |
\(4.26\pm0.05\) MeV |
\(K+\bar{K}, \pi^++\pi^-+\pi^0\) |
\(D^\pm\) |
\((c\bar{d},d\bar{c})\) |
\(0^{-}\) |
\(1869.3\pm0.4\) |
\(0.500\pm 0.007\) ps |
\(K+...\) |
\(D^0, \bar{D}^0\) |
\((c\bar{u},u\bar{c})\) |
\(0^{-}\) |
\(1864.5\pm0.4\) |
\(0.410\pm 0.002\) ps |
\(K+...\) |
\(B^0, \bar{B}^0\) |
\((b\bar{d},d\bar{b})\) |
\(0^{-}\) |
\(5279.4\pm0.5\) |
\(1.530\pm 0.009\) ps |
\(D+...\) |
\(B^0_s, \bar{B}^0_s\) |
\((b\bar{s},s\bar{b})\) |
\(0^{-}\) |
\(5367.5\pm1.8\) |
\(1.466\pm 0.059\) ps |
\(D^\pm_s+...\) |
\(J/\Psi\) |
\((c\bar{c})\) |
\(1^{-}\) |
\(3096.92\pm0.011\) |
\(93.4\pm2.1\) keV |
hadrons (87%), \(\mu+\mu^+, e+e^+\) (6%) |
\(\Upsilon\) |
\((b\bar{b})\) |
\(1^{-}\) |
\(9460.3\pm0.3\) |
\(31.98\pm2.63\) keV |
\(l+l^+\) |
4.1.2. los quarks#
Los quarks son los constituyentes de los hadrones.
Existen 6 quarks, agrupados en tres dupletes de isoespín debil.
La tabla de quarks
generación |
Q (e) |
||
|---|---|---|---|
u (2 MeV) |
c (1.2 GeV) |
t (170 GeV) |
\(\frac{2}{3}\) |
d (5 MeV) |
s (93 MeV) |
b (4.2 GeV) |
\(-\frac{1}{3}\) |
Cada quark está en un estado de un triplete de color (\(r, g, b\), rojo, verde y azul):
Por lo tanto hay 18 quarks y 18 anti-quarks.
Los estados de quark son, por helicidad \(\pm\), y color, \(a = r, g, b\):
Pero cada hadrón está en un singlete de color. Lo que limita las combinaciones permitidas de quarks en bariones y mesones.
4.1.3. Descubrimientos de los hadrones, quarks y el color#
1932 Chadwick descubre el neutrón.
1935 Yukawa postula que la fuerza entre nucleones se media con un \(\pi\).
1947 Powell descubre en las emulsiones nucleares el \(\pi\) y el \(\mu\).
1947 Observación del \(\pi\), \(K\).
1961 Gell-Mann predice la existencia del \(\Omega^-\) (que se descubre en 1968) con el modelo de SU(3) de sabor.
1964 Gell-Mann y Zweig postulan la existencia de los quarks.
1968 Descubrimiento de los quarks y la estructura de los nucleones en SLAC.
1974 Richter, Ting et al, Descubrimiento del \(J/\Psi\) en SLAC y Brookhaven.
1977 Lederman et al, Descubrimiento de \(\Upsilon\) en Fermilab.
1979 Descubrimiento del gluón en sucesos de tres jets (DESY).
1995 Descubrimiento del top en Fermilab en CDF.
Hitos importantes en la compresión de los hadrones:
1963 Cabibbo propone la mezcla de estados de masas y débiles en los quarks.
1964 Fitch, Cronin et al, violación de CP en sistema de kaones neutrons.
1973 Kobayashi, Maskawa para explicar la violación CP, proponen la matriz de mezclas que lleva su nombre.
1998 confirmación de violación CP en el sistema de \(B_0\) neutros en BaBar (SLAC) y Belle (KEKB).
4.2. Características de las interacciones fuertes#
4.2.1. Confinamiento#
Los quarks no se presentan aislados, siempre aparecen en parejas en mesones o tríos en bariones.
Sería facil identicar una partícula cargada con carga fraccionaria \(2/3, -1/3\) y no ha sucedido. Los quarks no son libres.
Este fenómeno se conoce como confinamiento.
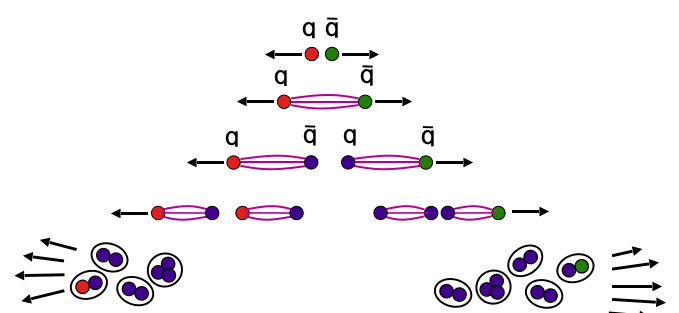
No existe una explicación analítica, pero podemos entenderlo como el hecho de que al separar dos quarks éstos están ligados fuertemente por los gluones, que actuarían como una «cuerda» estirada, que al romperse crearía un quark-antiquark en sus extremos de rotura (ver [MT10.4])
Matemáticamente veremos que la condición de confinamiento se traduce en que los quarks tienen que ser singletes de color.
4.2.2. Hadronización#
Cuando rompemos un hadrón en un choque de alta energía producimos una cascada de hadronización, que se denomina jet.
Esquema de hadronización [MT] |
Experimentalmente un jet es un corro de partículas que salen en un «cono» en la dirección del quark (o gluón) inicial.
La estructura y elementos del jet depende del quark que lo inició. Los jets de quarks pesados \(b, t\) son diferentes en topología a los de los ligeros \(u, d, s\).
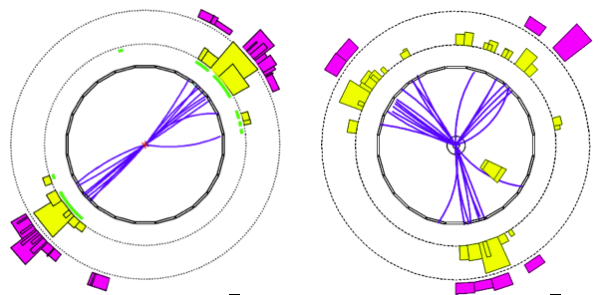
Sección trasnversal de dos eventos: 2 jets \(e+e^+ \to q+\bar{q}\) (izda) y 3 jets \(e+e^+\to q+\bar{q}+g\) (derecha) en OPAL (90’s) en LEP [MT, OPAL Collab] |
Los jets se caracterizan por su quark dependiendo de las partículas y características del jet.
En la figura se muestran dos sucesos \(e+e+\to 2\) jets y \(3\) jets en el plano transverso tomados por OPAL del LEP . Se aprecia como en el caso de 2 jets, estos sos opuestos. Los sucesos 3 jets se producen por la radiación de un gluón (que hadroniza produciendo un jet), son procesos \(q,\bar{q}, g\). Los jets de gluones presentan una estructura angular compatible con ser producidos por una partícula vectorial, de espín 1.
Para identificar jets en los datos de ATLAS y CMS, se emplean habitualmente algoritmos basados en el aprendizaje profundo (deep learning), como redes neuronales (neural networks).
El proceso de modelización de la hadronización es complejo y basado en la fenomenología.
4.2.3. Libertad asintótica#
Paradójicamente las constantes de acoplo ¡no son constantes!, dependen de la escala de energía de la interacción, aunque su dependencia es suave, logarítmica con el \(q^2\) (con el cuadrado de momento transferido). Su explicación se escapa al contenido del curso (ver [MT10.5, AB5.8]) y está relacionada con la escala a la que observamos la interacción, que convierte la constante en «efectiva». Pero si medimos la constante a una determinada escala podemos estimar cuánto vale a una escala superior.
La teoría cuántica de campos convivió durante décadas con un problema matemático grave: en el caso de que considerásemos en el propagador (por ejemplo del fotón) todos los posibles diagramas de Feynman de orden superior que podrían intervenir, nos encontraríamos que la suma de amplitudes no converge, esto es, ¡es infinita!
G.”t Hoof demostró en los 70’s que una teoría con simetría gauge puede reabsorber esos diagramas y proveer una amplitud de transición finita. Pero como consecuencia, la constante de acoplo, \(\alpha\), depende ahora de \(q^2\) de forma logarítmica. Este mecanismo se denomina renormalización.
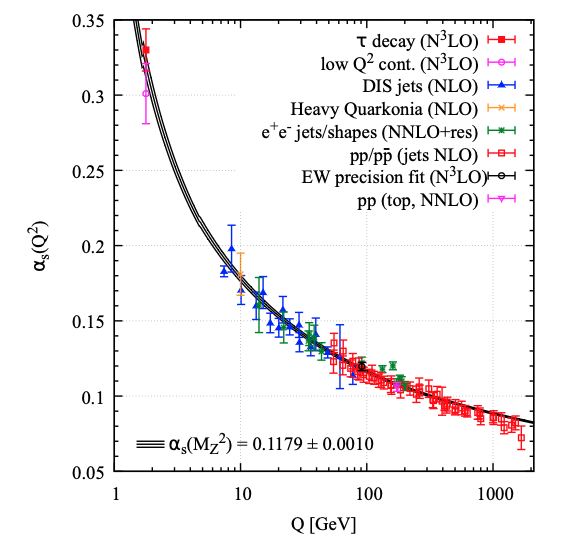
Valores experimentales de la constante de acoplo fuerte \(\alpha_s(q^2)\) en función de \(q\)
valores experimentales de \(\alpha_S(q^2)\) vs q [PDG] |
La constante de acoplo fuerte \(\alpha_S \sim 1\) a bajas energías, pero a las energías del LHC \(\alpha_S \sim 0.17\), lo que permite realizar algunos cálculos perturbativos en QCD válidos para el LHC.
Conforme la energía es mayor, menor es la constante de acoplo fuerte, y por lo tanto los quarks están más libres dentro de los hadrones, aunque nunca libres completamente, este fenómeno se denomina libertad asintótica.
Contrariamente la constante de acoplo electromagnética, \(\alpha\) ,y débil, \(\alpha_W\) decrecen con \(q^2\).
Nota: Debe existir una escala de energía \(\Lambda\) donde las constantes, al menos dos, sean iguales. En las teorías supersimétricas, las tres constantes se igualan a una determinada escala.
4.3. Estructura de los nucleones#
La estructura interna del protón (o neutrón) se estudia mediante experimentos de dispersión:
electrones (QED) |
débil |
fuerte |
\(e + p\) |
\(\nu + p\) |
\(p + p\) |
cada uno es sensible a diversas fuerzas (QED y débil), débil y fuerte respectivamente.
Los procesos se dividen en:
elásticos |
inelásticos |
\(e + p \to e + p\) |
\(e + p \to e + X\) |
Donde \(X\) indica la producción de diversos hadrones.
La dispersión inelástica se torna dominante conforme la energía aumenta.
A una determinada energía, los procesos inelásticos se corresponden con procesos elásticos de la sonda con los partones (quarks de valencia).
Conforme la energía de la sonda \(e, \nu, p\) aumenta, podemos exploramos escalas distintas del protón.
El protón como partícula “puntual” con spín \(1/2\) y carga \(+e\).
La distribución de carga, \(\rho(r)\), y momento magnético del protón.
La estructura de quarks de valencia (uud), que se llamaron partones.
Los quarks de valencia y el mar de gluones y quarks.
La estructura del protón se descubrió gracias a las pruebas \(e+ p \to e + X\) principalmente en SLAC en los 60’s [ver MT8, AB6.3]. La interacción es compleja porque es electro-débil.
También podemos estudiar la estructura de los nucleones a partir de las dispersiónes con \(\nu_\mu\) dado que solo interaccionan débilmente, y es más sencillo. Estos experimentos se realizaron en los 80’s [ver MT12.2-3].
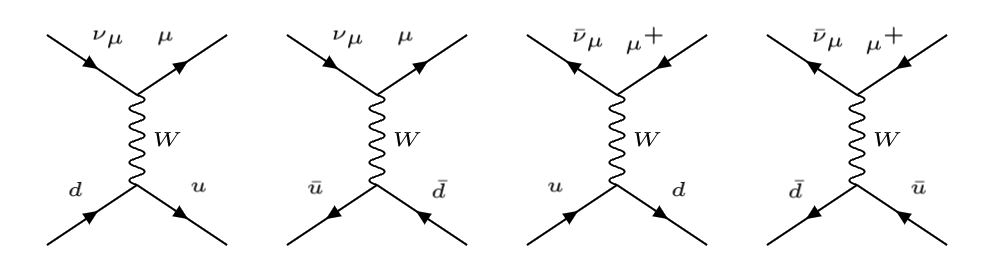
Los siguientes diagramas muestran las interacciones \(\nu_\mu, \bar{\nu}_\mu\) con \(q, \, \bar{q}\), con \(q=u, d\), del nucleón.
Diagramas de Feynman de la dispersión de \(\nu_\mu, \bar{\nu}_\mu\) con \(q, \bar{q}\) en corrientes cargadas |
Los cálculos de la sección eficaz, usando las reglas de los diagramas de Feynman, son relativamente sencillos en TCQ:
En el caso: \(\nu + q \to \mu + q'\):
Y con los anti-neutrinos, \(\bar{\nu} + q \to \mu + q'\)::
Este es, la razón entre ambas es simplemente:
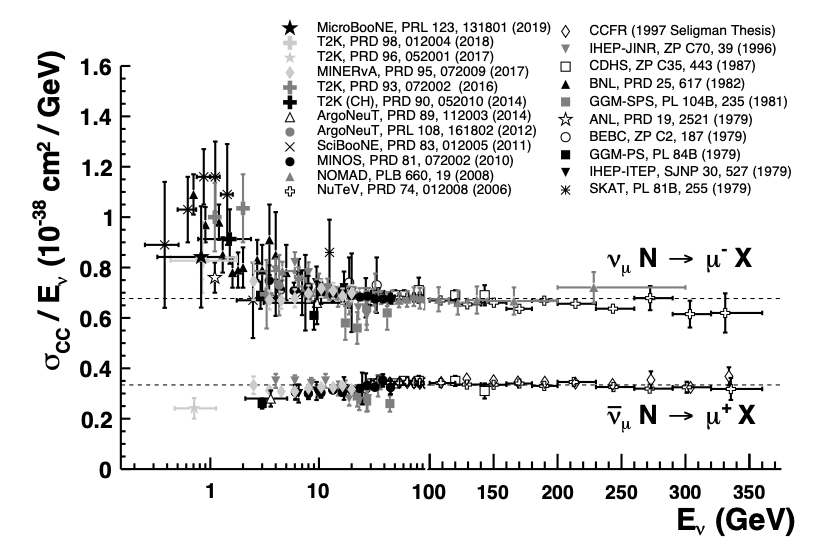
Los datos experimentales, de diversos experimentos a diferentes energías, son los siguientes
sección eficaces experimentales de \(\sigma(\nu_\mu +N \to \mu + X)/E_\nu, \; \sigma(\bar{\nu}_\mu) + N \to \mu^+ + X)/E_\nu\) vs \(E_\nu\) [PDG] |
Observamos:
la sección eficaz aumenta linealmente con \(E_\nu\), con \(s\)
la sección eficaz con \(\nu_\mu\) es un factor ~2 de la de los \(\bar{\nu}_\mu\)
El valor promedio:
Y la razón:
Los experimentos de dispersión \(e+p\) ya habían descubierto que la composición del protón es muy compleja. Esta formado por los quarks de valencia (\(uud\)), pero también por gluones y por pares quark, anti-quark del mar.
Sea \(f_q\) la fracción de quarks en el nucleón y \(f_{\bar q}\) la de anti-quarks. Podemos dar las secciones eficaces en un nucleón compuesto por \(q\) y \(\bar{q}\) por:
¡Notar que los neutrinos no interaccionan con los gluones sólo con los quarks y anti-quarks!
Con los valores experimentales anteriores obtenemos: $\(f_q \simeq 0.41, \;\; f_{\bar{q}} \simeq 0.1\)$
Concluimos que ¡El protón está compuesto en 41% de quarks y 10% de anti-quarks, el resto son gluones!
Lo que está en acuerdo con los experimentos \(e + p \to e + X\).
4.4. 6 Quarks de 3 colores#
4.4.1. aniquilación \(e+e^+\to f+\bar{f}\)#
La aniquilación \(e+e^+ \to q+\bar{q}\) es una de las pruebas principales de la existencia de los quarks de sabor y del número de color.
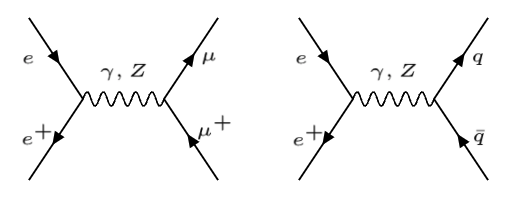
Los siguientes diagramas muestran las dos aniquilaciones, \(e + e^+ \to \mu+ \mu^+\) y \( e + e^+ \to q+\bar{q}\) que están mediados por los portadores neutros \(\gamma, Z\).
Diagramas de Feynman \(e+e^+ \to \mu+\mu^+\) (izda), \(e+e^+\to q+\bar{q}\) (derecha) |
Los propagadores asociados con fotón y el \(Z^0\) son respectivamente:
donde \(m_Z = 91.2\) GeV es la masa del \(Z\).
La importancia de los mediadores depende del cuadrado cuadri-momento transferido, \(q^2\).
Cuando \(q^2 \le m^2_Z\). El fotón domina y el propagador del \(Z\) es simplemente \(\propto 1/m^2_Z\).
Cuando \(q^2 \sim m^2_z\) la contribución de \(Z\) domina (es la región de la resonancia del \(Z\)).
En la zona intermedia, los dos diagramas contribuyen.
4.4.1.1. Sección eficaz \(e+e^+\to f+\bar{f}\).#
Consideremos en rango \(q^2\) de aniquilación que domina el fotón (QED).
El promedio del elemento de matriz, \(e+e^+\to \mu+\mu^+\) puede calcularse en TQC usando los diagramas de Feynman (ver [MT6.2]), damos simplemente su valor. en El CM
La situación es idéntica para la producción \(e+e^+ \to q+\bar{q}\). A excepción de que en el vértice de la corriente \((q, \bar{q})\) el factor asociado a la carga es \(+Q_q e\), donde \(Q_q\) es la carga del quark en unidades de \(e\) (carga).
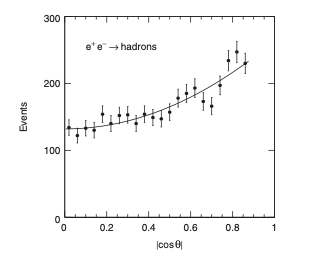
La figura muestra la distribución en \(|\cos\theta|\) de los eventos \(e+e^+\to q + \bar{q}\) en el CM del experimento CELLO (en DESY) en los 80’s en la región \(38.6 \le \sqrt{s} \le 46.5\) GeV.
Distribución angular \(e+e^+\to\) 2 jets en CELLO (DESY, 1987) [MT, AB, CELLO] |
que siguen la dependencia \(1+\cos^2\theta\).
Por supuesto, los dos quarks se manifiestan como dos jets.
4.4.2. Número de colores#
La carga eléctrica de los quarks entra en el vértice del elemento de matriz con un factor \(Q^2_q e^2\).
La sección eficaz \(e+e^+ \to q+\bar{q}\) (hadrones), dependerá para una energía disponible, \(\sqrt{s}\), y de los tipos de quarks (los distintos sabores) que se puedan crear con esa energía y de su carga.
Pero cada quark se presenta además en tres colores, por lo que por cada color de quark introduce un nuevo elemento de Matriz, esto es el el elemento de matriz total está multiplicado por \(N_c = 3\).
El factor que tenemos que añadir para un quark \(q\) es:
La sección total es:
donde \(q = u, d, s, c, b\) dependiendo de la energía \(\sqrt{s}\).
Cuando \(\sqrt{s}\) supera el umbrar de producción de un quark, \(q\), la sección eficaz \(\sigma(e+e^+\to q+\bar{q})\) se incrementará en \(N_c Q^2_q\)
Podemos comparar está sección eficfaz con la de \(\sigma(e+e^+ \to \mu+\mu^+)\), que son idénticas en valor a excepción del factor asociado a la carga y el número de colores de los quarks.
La razón \(R_\mu\) entre la producción de hadrones y pares \(\mu, \mu^+\) dependerá de:
\(u,d,s\) |
\(u, d, s, c\) |
\(u, d, s, c, b\) |
\(3 \left(\frac{4}{9}+\frac{1}{9}+\frac{1}{9} \right) = 2\) |
\(2 + \frac{4}{3} = \frac{10}{3}\) |
\(2 + \frac{5}{3} = \frac{11}{3}\) |
Cuestión: ¿Cómo serían estos factores si \(N_C = 1\) ?
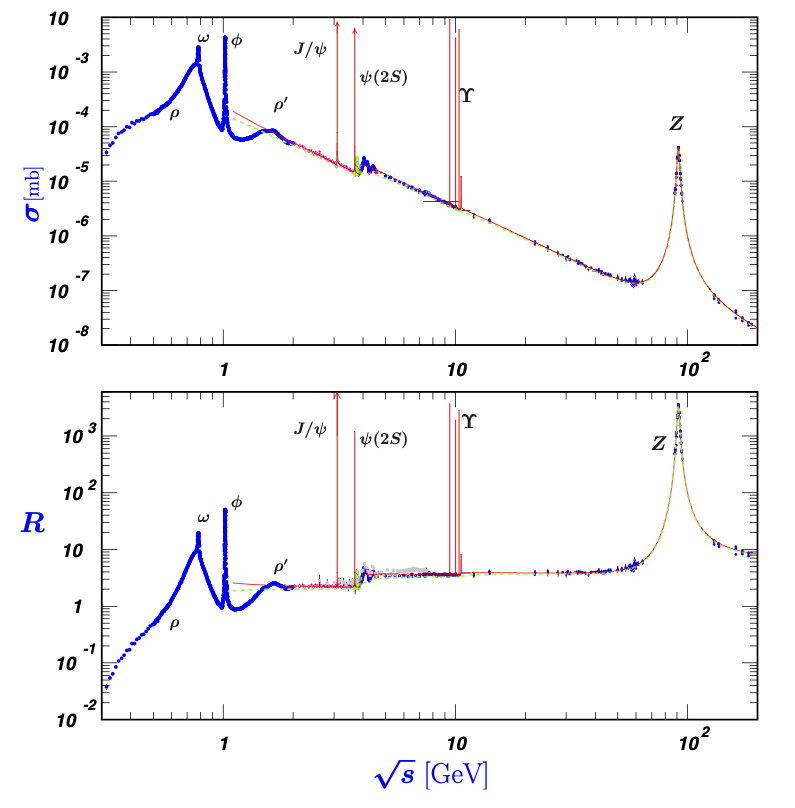
La figura muestra los datos experimentales y la predicción del modelo de quarks sencillo (línea punteada) y con correcciones de QCD (línea continua).
sección eficaz \(\sigma(e+e^+ \to \mathrm{hadrons})\) (arriba) y \(R_\mu\) (abajo) en función de \(\sqrt{s}\), datos y teoría (líneas) [PDG] |
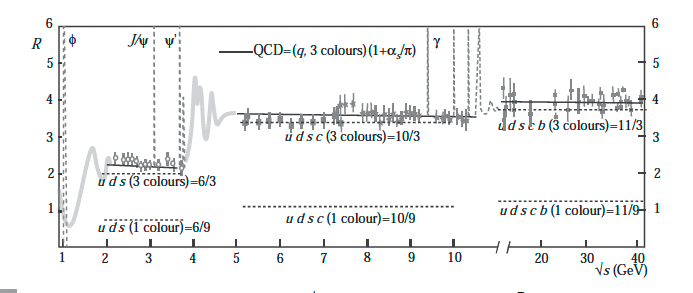
La figura muestra los datos experimentales y la predicción del modelo de quarks sencillo (línea punteada) y con correciones de QCD (línea continua) en las tres regiones relevantes: para los quarks ligeros (\(u, d, s\)), el quark \(c\) y el quark \(b\).
sección eficaz \(\sigma(e+e^+ \to \mathrm{hadrons})\) (arriba) y \(R_\mu\) (abajo) en función de \(\sqrt{s}\), datos y teoría (líneas) [AB6.3] |
Ovservamos:
la sección eficaz decrece con \(1/s\)
aparecen resonancias de mesones ligeros (con quarks \(u, d, s\)), y pesados, (\(J/\Psi, \Psi\)), y \(\Upsilon\) conforme producimos quarks \(c, b\) respectivamente.
la Razón \(R_\mu\) se incrementa con la aparición de un nuevo quark, con su carga y con sus tres colores. Lo que demuestra la existencia de los quarks, de sus cargas fracionadas y de que se presentan en 3 colores.
la correción adicional de QCD ajusta a los datos.
En el capítulo del Modelo Estándar discutiremos la resonancia del \(Z\) (en la derecha en las figuras).
Nota adicional: El efecto de la corrección en QCD se debe a que los gluones transmiten color. El buen ajuste demuestra que efectivamente es así.
4.5. Desintegraciones débiles de hadrones.#
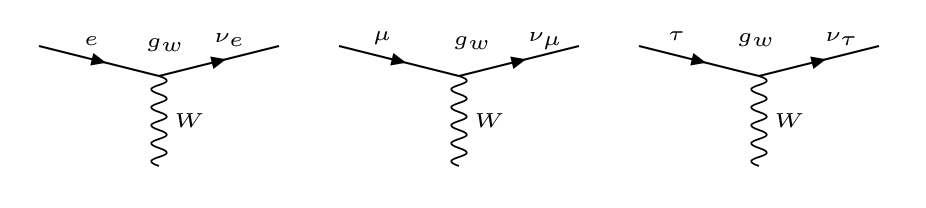
Sabemos que el bosón \(W\) se acopla con un leptón de arriba y abajo pero siempre de la misma generación.
Vimos (en el tema leptones) que la constante de acoplo es la misma para las tres generaciones \(g_W\), lo que llamamos universalidad leptónica.
En las desintegraciones débiles de los leptones vimos que la constante de acoplo de cada vértice era universal \(G^{(e)}_F = G^{(\mu)}_F = G^{(\tau)}_F\).
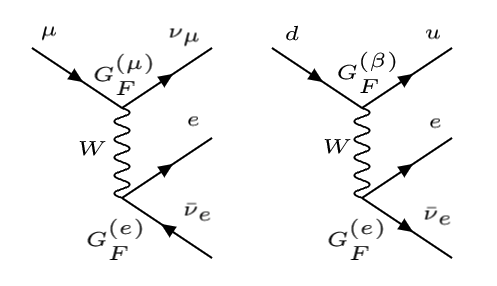
A partir de las medidades de las desintegraciones \(\beta\) obtenemos la constante de acoplo del vértice asociado a la corriente de los quarks, \(G^{(\beta)}_F\), que podemos comparar con \(G^{(\mu)}_F\) del vértice de las desintegraciones \(\mu \to \nu_\mu + e + \bar{\nu}_e\):
Diagramas de Feynman de desintegración \(\beta\) y del \(\mu\) |
que es un 5% más pequeña.
Cabibbo (1963) propuso que las interacciones débiles son universales para los auto-estados débiles \(d', s'\), pero que experimentalmente observamos los estados de masas \(d, s\) dentro de los hadrones. Entre ambos media una matriz de mezcla unitaria.
Si solo consideramos dos quarks abajo, la matriz es simplemente:
donde \(\theta_C\) es el ángulo de Cabibbo.
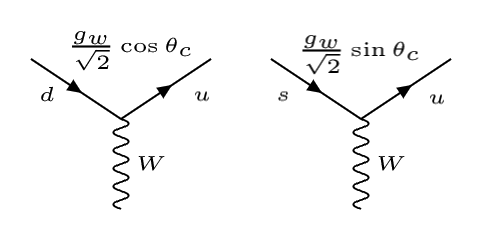
De tal forma que los vértices de las corrientes cargadas entre quarks serán:
Vértices débiles con el ángulo de Cabbibo |
La constante \(G_F^{(\beta)}\) estaría suprimida por un factor \(\cos^2 \theta_C\).
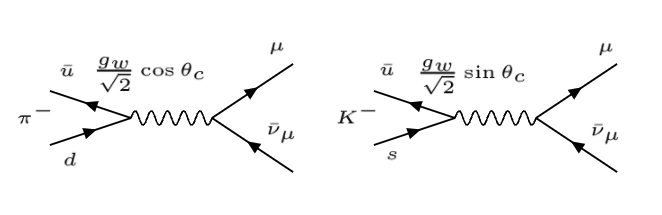
Esto explica la diferencia entre las anchuras de desintegración de \(\pi^- \to \mu + \bar{\nu}_\mu\) y \(K^- \to \mu + \bar{\nu}_\mu\).
Vértices débiles en la desitegración \(\pi^, K^-\) |
La razón de desintegración entre ambos estará suprimida por un factor \(\tan^2 \theta_c\).
El valor del \(\theta_C \sim 13\)º.
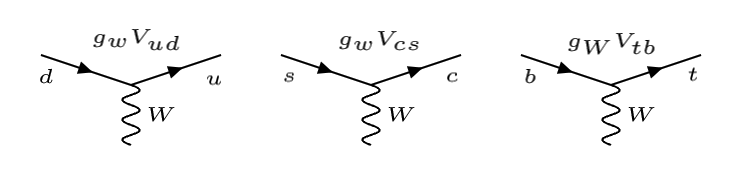
Ahora sabemos experimentalmente, que los quarks se acoplan con el \(W^\pm\) en pares de arriba y abajo entre las distintas generaciones:
La constante de acoplo ya no es universal si no que depende del par arriba y abajo que se acopla, \(g_W V_{ij}\), (donde \(i = \{u, c, t\}, j = \{d, s, b\}\)).
Vértices del \(W\) con parejas de quarks |
La extensión a 3 generaciones da lugar a la matriz, \(V_{CKM}\), de Cabibbo-Kobayashi-Maskawa (CKM).
Donde \(V\) es una matriz unitaria: \(V^\dagger V = I\), que queda definida por tres ángulos de rotación y una fase compleja.
Las corrientes débiles entre quarks \(u \to d\) son:
donde \(p_u, p_b\) son los cuatrimomentos de \(u, b\) respectivamente.
La matriz de CKM da lugar a una fenomenología muy rica entre hadrones donde existen ligaduras que deben cumplirse.
En particular la matriz debe ser unitaria.
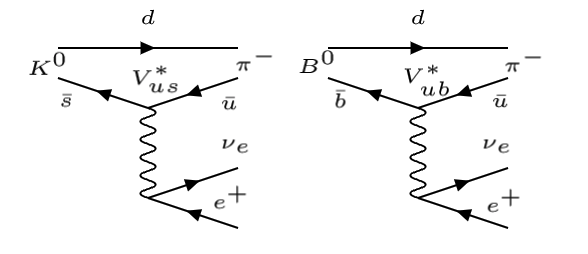
Por ejemplo, las siguientes desintegraciones permiten determinar por ejemplo \(|V_{us}|, |V_{ub}|\)
Diagramas de Feynman \(K^0 \to \pi^- + e^+ + \nu_e, \; B^0 \to \pi^- + e^+ + \nu_e\) |
Los valores experimentales de los elementos absolutos de la matriz CKM:
Observamos:
los valores diagonales son próximos a 1.
la mezcla entre las generaciones 1-2 es más intensa que entre la 1-3 y 2-3.
Si escribimos la matriz en términos de los tres ángulos de mezcla \(\theta_{12}, \theta_{13}, \theta_{23}\) y una fase compleja \(\delta\):
donde \(c_{ij} = \cos \theta_{ij}, \; s_{ij} = \sin \theta_{ij}\).
Los valores experimentales:
Los ángulos de mezcla son «pequeños». Existe una fase compleja \(\delta\), una constante de la Naturaleza, que dará lugar a una fenomenología muy rica de procesos de violación de carga y paridad en hadrones [ver MT14, AB8] que escapan an nivel de este curso.
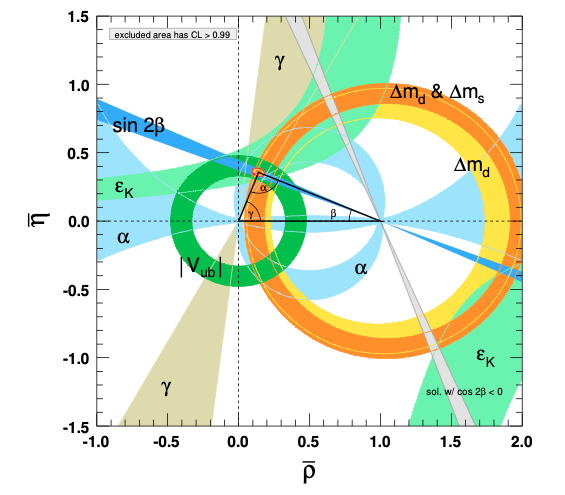
La siguiente figura muestra las medidas experimentales (áreas coloredas) al 99 % CL de diversos experimentos. Todos ellos coinciden en un punto (el del vértice marcado con el ángulo \(\alpha\)) en el plano complejo, que está relacionado con \(\delta\).
plano \((\bar \rho, \bar \eta)\) y medidas experimentales al 99% CL [PDG] |
4.6. Sobre la Cromo Dinámica Cuántica, QCD.#
Vimos antes al medir \(R_\mu\) que los quarks se presentaban en tres colores, que llamaros rojo, verde, y azul. En realidad son los nombres de cargas, no tiene nada que ver con los colores habituales.
La teoría detrás de las interacciones fuertes, Quantum Chromo Dynamics, QCD, se desarrolló en los 70’s por Gross, Politzer, Wilczek, Fritzsch, Gell-Mann, “t Hooft entre otros.
En QCD cada quark tiene un posible color: rojo, verde y azul, que podemos asignarlos como las componentes de un triplete.
Similar a los dupletes de spín:
De forma matemática podemos entender el espinor de Dirac, \(u(p)\) añadiéndole un triplete de color, \(c_a\):
con \(a = r, g, b\).
El duplete corresponde a la representación irreducible \({\bf 2}\) del grupo SU(2), que tenía tres generadores, \(T_i = \frac{1}{3}\sigma_i\), dados por matrices de Pauli, que obedecían a las reglas de conmutación del momento angular.
En SU(2) solo dos operadores conmutan, \(T^2, T_3\), el spin total y su tercera componente. Los estados irreducibles los etiquetábamos con \(T_3\). Las combinaciones de estados daban lugar a nuevos estados que se relacionaban con los originales via los coeficientes de Clesch-Gordan, que a su vez se obtenían de la aplicación de los operadores escalera.
El triplete de color es la representación irreducible de \({\bf 3}\) del grupo SU(3), que tiene 8 generadores, \(T_i = \frac{1}{2} \lambda_i\), dados por las matrices de Gell-Mann.
En SU(3) solo tres operadores conmutan \(T^2, T_3, Y\). Donde \(T_3\) es la tercera componente de color, \(Y\) es la hypercarga de color. Cada estado lo podemos etiquetar ahora con dos valores, \(T_3, Y\).
Cuando combinamos dupletes de SU(2) obteníamos un triplete y un singlete: \({\bf 2} \otimes {\bf 2} = {\bf 1}\oplus {\bf 0}\)
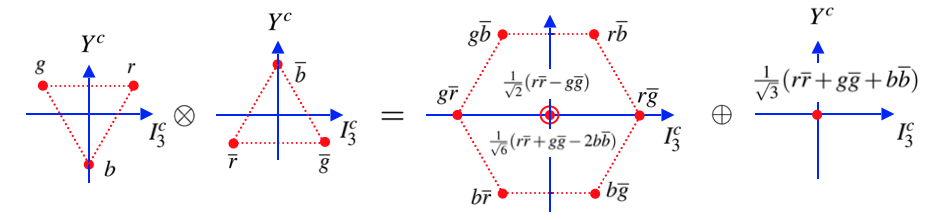
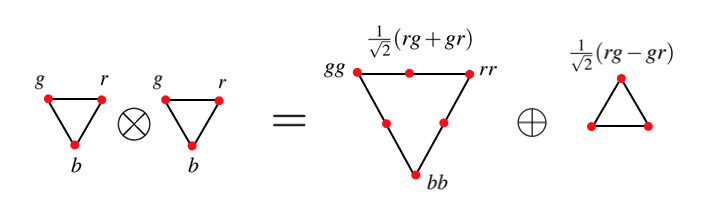
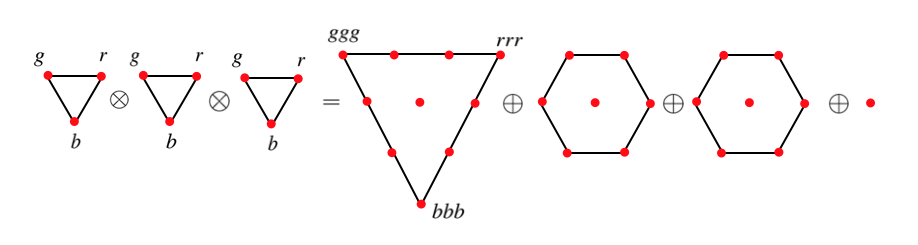
En la figura se muestra gráficamente la combinación de un triplete con un anti-triplete (\({\bf 3} \otimes {\bf \bar{3}})\), dos tripletes (\({\bf 3} \otimes {\bf 3}\)) y tres tripletes de color (${\bf 3} \otimes {\bf 3} \otimes {\bf 3}):
combinaciones de quark-antiquark (arriba), de dos quarks (medio) y tres quarks (abajo) [MT] |
QCD exige que los hadrones sean singletes de color, partículas sin color o blancas.
Las combinaciones que dan singletes son:
Podemos formar una partícula sin color:
con un trío de quarks, que son los bariones
con un par quark, anti-quark, que son los mesones.
4.6.1. Los diagramas de Feynman en QCD#
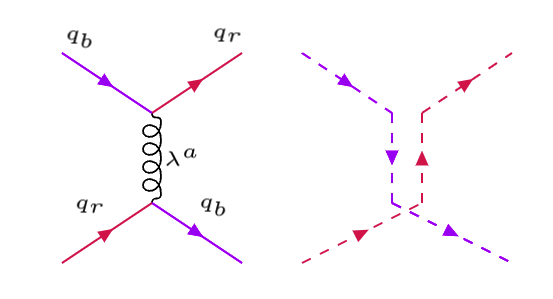
La siguiente figura muestra el diagrama de Feynman asociado a la dispersion por color \(q_b + q_r \to q_r + q_b\), donde gráficamente asociamos colores al gluón que intercambia los colores rojo y azúl, \((r,b)\) (ver [MT10.7, AB6.4]).
Diagrama de Feynman \(q_b +q_r \to q_r + q_b\) (izda) y sus líneas de color (derecha) |
el índice \(\alpha=1, \dots, 8\) corre sobre todos los posibles gluones.
La figura de la derecha muestra como los gluones intercambian cargas de color y son coloreados, al contrario que el fotón que no tiene carga eléctrica.
Nota: En los diagramas de Feynman los gluones se dibujan con un muelle.
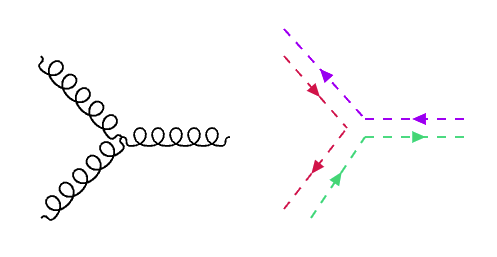
Los gluones al tener color, interaccionan entre ellos, por ejemplo, con un vértice \(ggg\) como el de la figura:
Ésto está asociado con el hecho de que su rango de acción sea muy corto, de fm.
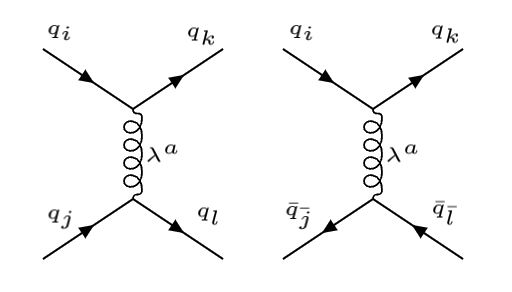
La siguiente figura muestra los diagramas de Feynman asociados a las dispersiones fuertes \(q_i + q_k \to q_j + q_l\) y \(q_i + \bar{q}_{\bar j} \to q_k + \bar{q}_{\bar{l}}\), donde los índices \(i, j, k, l\) corresponden a las cargas \(r, g, b\) y \({\bar j}, \bar{l}\) a las anti-cargas \({\bar r}, \bar{g}, \bar{b}\).
Diagramas de Feynman de las interaciones de color entre quarks y anti-quarks |
El factor asociado a los vértices de color en los diagramas de Feynman es:
donde \(g_S\) es la constante de acoplo fuerte, y \(\lambda^a\) es la matriz de Gell-Mann asociada a cada uno de los 8 gluones, \(a = 1, \dots, 8\).
El propagador de los gluones es:
donde \(\delta^{ab}\) garantiza que un mismo gluón media entre los dos vértices.
La corriente de los quarks que cambian de color \(i \to k\) y quedan mediadas por el gluón \(a\) queda:
donde \(p_a\) es el cuadrimomento del quark entrante y \(p_c\) el del saliente.
Notar que en la corriente sólo hemos introducido un factor de color que corresponde al elemento \(k, i\) de la matriz \(\lambda^a\):
4.6.2. QCD y QED#
QED (Electro Dinámica Cuántica) y QCD (Cromo Dinámica Cuántica) son teorías similares:
Son teorías con simetrías gauge locales que conservan paridad, carga y sabor.
Los mediadores son campos vectoriales sin masa.
Sin embargo son radicalemente diferentes:
El fotón no tiene carga eléctrica y su rango es infinito. No hay interacciones entre fotones.
Los gluones trasfieren color y por ello interaccionan entre ellos, dando lugar a que su rango de acción sea de fm, y solo sean libres partículas singletes de color.
El fotón proviene del generador del grupo U(1) que es la simetría local gauge del electromagnetismo.
Los fotones provienen de los generadores del grupo SU(3), las matrices de Gell-Mann, que es la simetría gauge local de QCD. Existen tres cargas en QCD, o colores, \(r, g, b\) y sus correspondientes anticargas \(\bar{r}, \bar{g}, \bar{b}\).
Nota: podemos entender \(r\) como una carga y pensar en \(r = +, \bar{r} = -1\), de forma similar a la carga eléctrica.