8. Extensión: Simetrías. Transformaciones Lorentz

import time
print(' Last version ', time.asctime() )

 Last version  Mon Dec  2 15:29:16 2024

8.1. Introducción

En la presente extensión revistaremos la importancia de las simetrías en Física, la transformación de Lorentz y las transformaciones unitarias.

Revisaremos en detalle los boost y rotaciones de Lorentz y desarrollaremos su representación espinorial.

Verificaremos después que las formas bilineales de norma y corriente femiónica transforman Lorentz de acuerdo con un escalar y un vector.

Posteriormente estudiaremos la inversión de Paridad y cómo afecta a las formas bilineales.

Finalmente discutiremos las inversión de Carga.

Las transformaciones internas basadas en grupos unitarios, esenciales para el entramado matemático del Modelo Estándar, si describen en la extensión [ext-grupos]

8.2. Simetrías y transformaciones

En Física las simetrías juegan un papel fundamental.

Las simetrías implican una transformación del sistema que lo deja indistinguible. Por ejemplo, una esfera tiene simetría esférica, al rotar una esfera sin marcas no podemos saber si se esta rotó.

Las simetrías en Física implican la invariancia matemática del lagrangiano (o equivalentemente dl hamiltoniano, o de las ecuaciones de movimiento) bajo las transformaciones asociadas.

Por un lado, sabemos que las ecuaciones de movimiento son iguales en sistemas inerciales, lo que implica que las ecuaciones deben ser invariantes bajos transformaciones de Lorentz.

Por otro, en mecánica cuántica describimos los sistemas físicos por estados, y sus observables a través de la norma. Por lo tanto las transformaciones válidad son aquellas que preservan la norma o unitariedad. Estas simetrías están relacionadas con la teoría de grupos. Asl estudiar los grupos identificaremos sus estados fundamentales que los asociaremos con las distintas partículas.

Las simetrías pueden ser continuas o discretas. Las simetrías continuas van a tener asociada por el teorema de Noether una cantidad conservada.

Las transformaciones de Lorentz propias (como las rotaciones o boosts) son cotinuas.

Mientras que la inversión de paridad es impropia y discreta. También la inversión por carga es una simetría discreta.

8.2.1. Transformaciones de Lorentz

Sabemos que las ecuaciones del movimiento deben ser iguales independientemente del sistema inercial que eligamos. Esto es, son invariantes bajo transformaciones de Lorentz.

Exigiremos siempre que nuestra teoría, nuestro lagrangiano, sea invariante Lorentz.

Las transformaciones de Lorentz son aquellas que dejan invariante la norma de un vector espacio-temporal usando la métrica de Minkowski.

\[ x'^{\mu} = \Lambda^{\mu}_{\;\;\nu} x^\nu \]

se cumple: $\( x'^\mu g_{\mu\nu} x'^\nu = x^\mu g_{\mu\nu}x^\nu \)\( donde \)g_{\mu\nu}$ es la métrica de Minkowsky.

Las transformaciones de Lorentz pueden ser continuas y propias como los boost o rotaciones y otras discretas e impropias como la inversión por paridad.

La siguiente sección desarrolla en detalle las transformaciones de Lorentz propias. La extensión [ext-cpt] cubre la inversión por paridad.

8.2.2. Unitariedad

En mecánica cuántica una transformación asociada un estado a otro del espacio de Hilbert, mediante un operador \(U\).

\[ | \psi \rangle \to | \psi' \rangle = U \; | \psi \rangle \]

Y la información física relevante (que sea observable) se obtiene a partir del cuadrado del producto \(|\langle \phi | \psi \rangle |^2\), lo que lleva (teorema de Wigner) a que las transformaciones posibles sean unitarias o anti-unitarias (unitaria y anti-lineal)

\[ |\langle \phi' | \psi' \rangle|^2 = |\langle \phi | U^\dagger U | \psi \rangle|^2 \]

La actuación del operador unitario, \(U\) y anti-unitario \({\tilde U}\) afectan al producto escalar de la siguiente forma:

\[\begin{split} \langle \phi | U^\dagger U | \psi \rangle = \langle \phi | \psi \rangle \\ \langle \phi | {\tilde U}^\dagger {\tilde U} | \psi \rangle^ = \langle \phi | \psi \rangle^* \end{split}\]

Ambas dejan invariante la norma \(|\langle \phi | \psi \rangle |^2\).

En mecánica cuántica exigiremos que las transformaciones son las unitarias (y en ciertos casos anti-unitarias). Un operador unitario cumple:

\[ U^\dagger U = I, \;\; U^{-1} = U^{\dagger} \]

Una operación anti-unitaria, \({\tilde U}\), toma el complejo conjugado:

\[ {\tilde U} \, \alpha | \psi \rangle = \alpha^* | \psi \rangle \]

Los operadores anti-unitarios hay que tratarlos con cuidado.

Las transformaciones continuas son unitarias. Las anti-unitarias solo aparecen en transformaciones discretas, la más relevante de ellas es la inversión temporal.

8.2.2.1. Transformación activa y pasiva

Podemos entender las transformaciones como activas o pasivas. Las activas transforman el estado, mientras que las pasivas transforman el sistema de referencia.

Cuando verificamos una simetría de forma activa, verificamos que el comportamiento del estado transformado es el mismo que el original, mientras que de forma pasiva, verificamos que describimos el comportamiento del estado con las mismas ecuaciones en el sistema de coordenadas original y transformadio.

Si hacemos una rotación activa un punto \({\bf x}\) se traslada a otro punto \({\bf x}'\), pero los dos los damos en el mismo sistema de coordenadas, \(\{{\bf e}_i\}\). Mientras que cuando hacemos una rotación pasiva, rotamos los ejes de coordenadas y expresamos un mismo punto \(x\) en el sistema inicial \(\{{\bf e}_i\}\) o rotado \(\{{\bf e}'_i\}\). En las transformaciones activas pensamos en que un punto se traslada en otro y no en un cambio de coordenadas.

Asi la rotación activa de un ángulo \(\theta\) alrededor de \(z\) en sentido anti-horario nos dice que el punto original \((1, 0)\) se traslada a \((\cos \theta, \sin \theta)\). Mientras que una rotación pasiva expresaríamos el mismo punto como \((1, 0)\) en el sistema original y \((\cos \theta, -\sin \theta)\) en el nuevo sistema de coordenadas transformado, rotado respecto al original un ángulo \(\theta\) en sentido anti-horario alrededor del eje \(z\).

Es más natural introducir las transformaciones de Lorentz desde un punto de vista pasivo, como cambio de coordenadas, pero resulta más conveniente tomar un punto de vista activo cuando se trabaja con conceptos más abstractos como campos.

En la literatura aparecen las transformaciones activas y pasivas y a veces no se indica de cuál se trata. Es importante saber siempre con qué tipo de transformación se está trabajando. Nosotros usaremos transformaciones activas.

8.2.2.2. Transformación de estados (Schrödinger) o de operadores (Heidelberg)

Podemos no obstante considerar dos tipos de transforemaciones activas, según la versión de Schrödinger o la de Heidelberg.

En la de Schrödenger transformamos los \(| \psi \rangle\), mientras que en la de Heidelberg, transformamos los operadores, \(O\), (visión de Heidelberg). Esta última es la más habitual en TCQ.

Una transformación unitaria, queda en la versión de Schrödinger: $\( | \psi \rangle \to | \psi' \rangle = U \, | \psi \rangle, \;\;\; O \to O \)$

y en la versión de Heidelberg: $\( | \psi \rangle \to \ \psi \rangle, \;\;\; O \to O' = U^{-1} O U = U^\dagger O U \)$

Decimos que un sistema tiene una determinada simetría si la transformación asociada, \(U\), deja invariante el valor esperado de un operador hermítico (esto es observable), \(O\). Esto se cumple si \(U\) y \(O\) conmutan, \([U, O] = 0\).

\[ \langle \psi | O | \psi \rangle \to \langle \psi | U^\dagger O U | \psi \rangle = \langle \psi | U^\dagger U O | \psi \rangle = \langle \psi | O | \psi \rangle \]

En el caso de que \(U\) sea el hamiltoniano \(H\), entonces los auto-estados de \(O\) son estacionarios (no cambian con el tiempo).

\[ i \hbar \frac{\mathrm{d}}{\mathrm{d}t} \langle O \rangle = \langle [O, H]\rangle \]

Para las transiciones entre estados, inicial \(| i \rangle\), a final, \(| f \rangle\), calculamos el elemento de matriz de la matriz de transición \(M\), \(\langle f | M | i \rangle\).

Si \(M\) conmuta con \(U\), y los estados \(|i\rangle, | f \rangle\) son autoestados de \(U\) con autovalores \(u_i, u_f\) respectivamente, entonces tenemos una ley de conservación:

\[ 0 = \langle f | [U, M] | i \rangle = (u_f - u_i) \langle f | M | i \rangle \]

Los autovalores, antes y después de la interacción, \(u_f, u_i\) deben ser iguales.

8.2.3. Teorema de Noether

El teorema de Noether afirma que un sistema con una simetría continua (por ejemplo rotación) tiene una cantidad conservada asociada (para la rotación sería el momento angular total).

Si la simetría es continua, podemos expresarla a partir de transformaciones infinitesimales, esto es, sea \(\alpha\) pequeña:

\[ U(\alpha) \simeq e^{i\alpha G} \simeq I + i \alpha G \]

Donde \(G\) son los generadores del la transformación que definen un grupo y sus reglas de conmutación definen las reglas del grupo.

La unitariedad \(U\) implica la hermicidad de \(G\).

\[ U^\dagger U = (I - i \alpha G^\dagger) (I + i \alpha G) \simeq I + i \alpha (G - G^\dagger) = I \]

Luego:

\[ G^\dagger = G \]

Al ser hemíticos, los generadores son observables.

8.2.4. Transformaciones discretas e inversiones

Las transformaciones discretas no se conectan continuamente con la identidad.

Las inversiones son aquellas transformaciones discretas que nos devuelven si las aplicamos dos veces seguidas al sistema original, por ejemplo, la inversión por paridad o por carga.

\[ | \Psi \rangle \to U_I \, |\Psi \rangle \to (U_I)^2 |\Psi \rangle = \eta \, |\Psi \rangle \]

donde \(\eta\) es una fase compleja sin implicaciones físicas.

Las inversiones tienen asociadas un operador unitario \(U_I\). El operador puede introducir una fase al operar sobre un autoestado, \(U_I |\psi \rangle = \eta_I | \psi \rangle\). En general la fase es espúrea, no tiene implicaciones físicas, pero en determinados casos puede ser o tomarse por convención como \(\pm 1\). [CHECK]

cuestión: A partir de los estados \(| \psi_1 \rangle, \, | \psi_2 \rangle\) que bajo una inversión \(U_I\) se transforman como \(| \psi_1 \rangle \leftrightarrow | \psi_2 \rangle\), escribe los autoestados de \(U_I\) y sus autovalores.

8.2.4.1. cantidades conservadas

Si \(U_I\) es hermítico y observable, exite también una cantidad que se conserva.

En el caso de multiples estados, la cantidad conservada es multiplicativa, el producto de las individuales, mientras que para el caso de transformaciones continuas era aditiva.

En el caso de que \(G\) sea un generador de una transformación continua, dada por \(U = e^{i\theta G}\), y \(| \psi_1 \rangle, | \psi_2 \rangle\) dos estados con autovalores \(g_1, g_2\) de \(G\) respectivamente.

\[ G | \psi_1 \rangle = g_1 | \psi_1 \rangle, \;\;\; G | \psi_2 \rangle = g_2 | \psi_2 \rangle \]

El estado dado por \(|\psi_1 \rangle, \psi_2 \rangle\) es también autoestado de \(G\) con autovalores \(g_1+g_2\):

\[ U | \psi_1 \psi_2 \rangle = e^{i\theta G} |\psi_1 \psi_2 \rangle = (e^{i\theta G} |\psi_1 \rangle) (e^{i\theta G} |\psi_2 \rangle) = e^{i \theta (g_1+g_2)} | \psi_1 \psi_2 \rangle \]

esto es:

\[ G | \psi_1 \psi_2 \rangle = (g_1+g_2) | \psi_1 \psi_2 \rangle \]

Mientras que para el caso de una inversión con operador hermício sea \(U_I\), siendo \(| \psi_1 \rangle, | \psi_2 \rangle\) dos estados con autovalores \(u_1, u_2\) de \(G\) respectivamente,

\[ U_I | \psi_1 \rangle = u_1 | \psi_1 \rangle, \;\;\; U_I | \psi_2 \rangle = u_2 | \psi_2 \rangle \]

obtenemos:

\[ U_I | \psi_1 \psi_2 \rangle = U_I |\psi_1 \psi_2 \rangle = (U_I |\psi_1 \rangle) (U_I |\psi_2 \rangle) = u_1 u_2| \psi_1 \psi_2 \rangle \]

Luego la cantidad conservas en inversiones es multiplicativa.

8.3. Transformaciones de Lorentz

Las transformaciones de Lorentz son transformaciones del espacio-tiempo, que preservan el producto escalar de los cuadri-vectores usando la métrica de Minkowski, y que en el espacio-tiempo se representan con matrices que denotamos como \(\Lambda\).

La transformación de un caudri-vector, \(x^\mu\), o de un cuadri-momento, \(p^\mu\), viene dada por:

\[\begin{split} x' = \Lambda \, x, \;\;\; x'^\mu = \Lambda^{\mu}_{\;\;\nu} \, x^\nu \\ p' = \Lambda \, p, \;\;\; p'^{\mu} = \Lambda^{\mu}_{\;\;\nu} \, p^{\nu} \end{split}\]

donde los índices \(\mu, \nu\) hacen referencia a las columnas y filas respectivamente de la matriz \(\Lambda\).

Las transformaciones de Lorentz preservan el producto escalar:

\[\begin{split} x' \cdot y' = x \cdot y, \\ (\Lambda^{\rho}_{\;\;\mu} \, x^\mu) \, g_{\rho\sigma} \, (\Lambda^{\sigma}_{\;\;\nu} \, y^\nu) = g_{\mu\nu} \, x^\mu y^\nu \end{split}\]

Esto es:

\[ g_{\rho\sigma} \Lambda^{\rho}_{\;\;\mu} \Lambda^{\sigma}_{\;\;\nu} = g_{\mu\nu} \]

O en forma matricial:

\[ \Lambda^{T} g \Lambda = g \]

Además existe la transformación inversa \(\Lambda^{-1}\)

\[ \Lambda \, \Lambda^{-1} = I, \;\; \Lambda^{\nu}_{\;\;\rho} (\Lambda^{-1})^{\rho}_{\;\; \mu} = \delta^{\nu}_{\;\;\mu} \]

8.3.1. Transformaciones propias e impropias

Sabemos que las transformaciones propias de Lorentz corresponden a las rotaciones en el espacio y los boost. Esto implica que: $\( \det(\Lambda) = 1 \)$ las transformaciones propias que están conectada de forman continua con la identidad.

Mientras que la inversión por paridad es una transformación de Lorentz impropia, donde $\( \det(\Lambda) = -1 \)$ y en este caso no hay conexión continua con la identidad.

Genéricamente el grupo de Lorentz son las matrices ortogonales que preservan la métrica de Minkowski, \(g_{\mu\nu}\), o en otras palabras, preservan el producto escalar de dos cuadrivectores, esto es, la matrices cumplen:

\[ \Lambda^T g \Lambda = g \]

El grupo de Lorentz se denota como \(O(1,3)\).

De la condición anterior se sigue:

\[ \det(\Lambda) = \pm 1 \]

Las transformaciones con \(\det(\Lambda) = +1\) forman un subgrupo, llamado \(SO(1, 3)\), el de transformaciones propias. Este subgrupo incluye las rotaciones y los boosts.

Las transformaciones con \(\det(\Lambda) = -1\) se llaman impropias, pero no forman un subgrupo porque no contienen el elemento identidad \(I\). La transformación de la inversión de paridad es impropia.

8.3.2. Transformaciones activas y pasivas.

La matriz asociada a una rotación activa de \(\theta\) alrededor del eje \(z\) (en sentido antihorario) y un boost activo en z con velocidad \(\beta\) son respectivamente:

\[\begin{split} \Lambda(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 1 & 0 & 0 & 1 \end{pmatrix} \;\;\; \Lambda(\beta) = \begin{pmatrix} \gamma & 0 & 0 & \gamma \beta \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \gamma \beta & 0 & 0 & \gamma \end{pmatrix} \end{split}\]

En una rotación activa alredor del eje \(z\) rotamos un ángulo \(\theta\) en sentido antihorario, lo que lleva al punto original \((1, 0, 0)\) en \((x, y, z)\) a transformarse en \((\cos \theta, \sin \theta, 0)\).

En un boost activo convertimos una partícula en reposo, con cuadri-momento \(p = (m, {\bf 0})\), en una partícula en movimiento con velocidad \(\beta\) en dirección \(\hat{{\bf v}}\) cuyo cuadrimomento es \(p' = (E, {\bf p}) = (\gamma m, \gamma \beta \hat{{\bf v}}\)).

El cambio de una transformación activa a pasiva -y viceversa- implica cambiar \(\theta \to - \theta\) y \(\beta \to -\beta\) en las matrices de sus representaciones.

Ejercicio: Comprueba \(\Lambda^T g \Lambda = g, \;\; \Lambda^{-1} \Lambda = I\) con las representaciones de \(\Lambda(\theta)\) y \(\Lambda(\beta)\)

8.3.3. Generadores de rotaciones y boosts

Las transformaciones de Lorentz propias se pueden construir a partir de la sucesión de transformaciones infinitesimales.

Estas transformaciones dependen de tres posibles ángulos de rotación \(\vec{\theta}\) alrededor de cada eje y de las tres componentes de la velocidad \(\vec{\beta}\).

8.3.3.1. Generadores de rotaciones

La rotación de un angulo infinitesimal \(\theta\) a lo largo del eje \(z\) viene dada por:

\[\begin{split} \Lambda(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & -\theta & 0 \\ 0 & \theta & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} + \theta \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \end{split}\]

Podemos dar la rotación anterior como:

\[ \Lambda(\theta) \equiv e^{i\theta J_3} \simeq I +i \theta J_{3}, \]

donde:

\[\begin{split} \;\; J_{3} \equiv -i \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \end{split}\]

A \(J_3\) lo llamamos el generador de las rotaciones en torno al eje \(z\).

Podemos dar la rotación de un ángulo \(\theta\) en torno a \(z\) como una sucessión de rotaciones infinitesimales. La matriz que representa la rotación, \(\Lambda(\theta)\), la podemos dar como el producto de las matrices de rotaciones infinitesimales.

De esta forma definimos la rotación a lo largo del eje \(y\) de un ángulo \(\theta\) como:

\[ \Lambda(\theta) \equiv e^{i \theta J_3} \equiv \sum_{k=0} \frac{(i \theta)^k}{k!} (J_3)^k \]

Dado que:

\[ \Lambda(\theta) = \Lambda\left(\sum_N \frac{\theta}{N}\right) = \prod_{N} \Lambda\left(\frac{\theta}{N}\right) = \lim_{N \to \infty} \left(I + i \frac{\theta}{N}J_3 \right)^N \]

Si separamos la serie en términos pares e impares:

\[\begin{split} I + \sum_{k=1} i^{2k} \frac{\theta^{2k}}{2k!} (J_3)^{2k} + \sum_{k=0} i^{2k+1} \frac{\theta^{2k+1}}{(2k+1)!} (J_3)^{2k+1} = \\ I + \sum_{k=1} (-1)^k \frac{\theta^{2k}}{2k!} (J_3)^{2k} + i \sum_{k=0} (-1)^k \frac{\theta^{2k+1}}{(2k+1)!} (J_3)^{2k+1} \end{split}\]

y haciendo uso de:

\[\begin{split} (J_3)^{2k} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \equiv I_{12}, \;\; (J_3)^{2k+1} = J_3, \end{split}\]

Obtenemos:

\[ I + \cos \theta \, I_{12} + i \sin \theta \, J_3, \]

Y de forma explícita:

\[\begin{split} \Lambda(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}, \end{split}\]

8.3.4. generadores de boosts

Vamos a determinar ahora la matriz asociada a un boost, \(\Lambda(\eta)\).

Definimos primero el parámetro \(\eta\), llamado rapidez, como \(\beta = \tanh \eta\), lo que implica:

\[ \gamma = \cosh \eta, \;\; \beta = \tanh \eta, \;\; \gamma \beta = \sinh \eta. \]

Notar que el rango de \(\beta\), que es \((-1, 1)\), se traslada en \(\eta\) en \((-\infty, \infty)\).

Decimos que el grupo de Lorentz no es compacto porque los valores de \(|\beta| = 1\) no son posibles, esto es el intervalo de \(\beta\) es abierto.

La transformación de Lorentz de un boots en \(z\) con velocidad \(\beta\) o rapidez \(\eta\) queda:

\[\begin{split} \Lambda(\eta) = \begin{pmatrix} \cosh \eta & 0 & 0 & \sinh \eta \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \sinh \eta & 0 & 0 & \cosh \eta \end{pmatrix} \end{split}\]

que podemos dar como sucesivos boost infinitesimales en la dirección \(z\)

\[\begin{split} \Lambda(\eta) = e^{i \eta K_3}, \;\; K_3 = -i \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} \end{split}\]

donde \(K_3\) es el generador de los boost en \(z\).

A partir de:

\[ \Lambda(\eta) = e^{i\eta K_3} \equiv \sum_{k} \frac{(i\eta)^k}{k!} \, (K_3)^k \]

separando en términos pares e impares:

\[\begin{split} I + \sum_{k=1} (-1)^{k} \frac{\eta^{2k}}{2k!} (K_3)^{2k} + i \sum_{k=0} (-1)^k \frac{\eta^{2k+1}}{(2k+1)!} (K_3)^{2k+1} = \\ \end{split}\]

y dado que:

\[\begin{split} (K_3)^{2k} = (-1)^k \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \equiv (-1)^k I_{03}, \;\; (K_3)^{2k+1} = (-1)^k K_3 \end{split}\]

obtenemos

\[\begin{split} \Lambda(\eta) = I + \sum_{k=1} \frac{\eta^{2k}}{(2k)!} \, I_{03} + i \sum_{k=1} \frac{\eta^{2k+1}}{(2k+1)!} \, K_3 = \\ \cosh \eta + i \sinh \eta K_3 \end{split}\]

de forma explícita:

\[\begin{split} \Lambda(\eta) = \begin{pmatrix} \cosh \eta & 0 & 0 & \sinh \eta \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \sinh \eta & 0 & 0 & \cosh \eta \end{pmatrix} \end{split}\]

Así pues, las transformaciones de Lorentz quedan definidas de forma genérica con un ángulo de rotación \(\theta\) alrededor de un eje \(\hat{{\bf n}}\) en sentido antihorario, y un boost de rapidez \(\eta\) en la dirección \(\hat{\bf v}\); y con sus correspondientes generadores \({\bf J}, {\bf K}\).

\[ \Lambda(\theta \, \hat{{\bf n}}+ \eta \, \hat{{\bf v}}) = e^{i (\theta {\hat{\bf n}} \, {\bf J} + {\eta \hat{\bf v} \, {\bf K}})} \]

Las expresiones de los generadores son:

\[\begin{split} J_1 = -i\begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 \end{pmatrix}, \;\; J_2 = -i\begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{pmatrix}, \;\; J_3 = -i\begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}, \\ K_1 = -i\begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}, \;\; K_2 = -i\begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}, \;\; K_3 = -i\begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix}. \end{split}\]

Ejercicio: Comprueba que:

\[ [J_i, J_j] = i\epsilon_{ijk} J_k, \; [K_i, K_j] = -i\epsilon_{ijk} J_k, \; [J_i, K_j] = i\epsilon_{ijk} K_k \]

8.4. Representación espinorial

Los campos que componen las física de partículas tienen naturaleza escalar, vectorial, y espinorial.

Este último corresponde a las soluciones de la ec. de Dirac, que son vectores de 4 componentes con elementos complejos.

Conocemos como se transforman los campos escalares y vectoriales.

La cuestión es ¿cómo lo hacen los campos espinoriales?

Los espinores van a tener asociada una representación en su espacio vectorial de las transformaciones de Lorentz. Esto es para una transformación de Lorentz con matriz \(\Lambda\) en el espacio-tiempo le corresponde una matrix \(S(\Lambda)\) en el espacio spinorial (complejo de 4 dimensiones). Esto es:

\[ \Psi(x) \to \Psi'(x) = S(\Lambda) \, \Psi(\Lambda^{-1} x) \]

8.4.1. representación de los campos

Recordemos que si hacemos una transformación activa, esto es transformamos los campos manteniendo las coordenadas, un campo escalar, \(\phi(x)\), y otro vectorial, \(A^\mu(x)\), transforman de la siguiente manera:

\[\begin{split} \phi'(x) = \phi(\Lambda^{-1} x)\\ A'^\mu(x) = \Lambda^{\mu}_{\;\; \nu} \, A^{\nu} (\Lambda^{-1} x) \end{split}\]

Por ejemplo, el campo escalar transformado \(\phi'(x)\) vale en un punto \(x\) lo que vale el campo en el punto de origen antes de la transformación, \(\phi(\Lambda^{-1} x)\).

Mientras que el campo vectorial transformado \(A'^\mu(x)\) corresponde en \(x\) al campo \(A^\nu(\Lambda^{-1} x)\) que había el punto original \(\Lambda^{-1}x\) al que rotaremos por \(\Lambda^\mu_{\;\;\nu}\).

[ADD] Dibujo de la transformación activa de un campo escalar y vectorial

La cuestión ahora es ¿Cómo transforma el espinor solución de la ec. de Dirac? ¿Cómo se transforma un campo espinorial, \(\Psi(x)\), frente a transformaciones Lorentz?

Como \(\Psi(x)\) tiene cuatro componentes complejas, la representación de la transformación de Lorentz en el espacio espinorial será una matriz compleja \(4\times4\) que dependera de \(\Lambda\), que denotamos \(S(\Lambda)\) y que transformará linealmente el campo:

\[ \Psi'(x) = S(\Lambda) \, \Psi( \Lambda^{-1}x) \]

La representación espinorial debe cumplir las mismas reglas multiplicativas del grupo de Lorentz en el espacio-tiempo.

La transformación que corresponde a dos transformaciones consecutivas \(\Lambda = \Lambda_2 \Lambda_1\) es:

\[ \Psi'(x) = S(\Lambda) \, \Psi( \Lambda^{-1} x) = S(\Lambda_2) S(\Lambda_1) \, \Psi(\Lambda_1^{-1} \Lambda_2^{-1} x) \]

Esto significa que las matrices \(S(\Lambda)\) forman una representación del grupo de Lorentz:

\[\begin{split} \Lambda \to S(\Lambda), \\ \Lambda =\Lambda_2 \,\Lambda_1 \to S(\Lambda) = S(\Lambda_2) \, S(\Lambda_1), \\ \Lambda^{-1} \,\Lambda = I \to S(\Lambda^{-1}) \, S(\Lambda) = I \end{split}\]

A cada transformación de Lorentz le corresponde una matriz en el espacio espinorial que la representa, y la matriz que representa la sucesión de las dos transformaciones es el producto de las matrices de cada transformación por separado.

A partir de ahora no explicitaremos la dependencia de \(S\) con \(\Lambda\) por simplicidad.

8.4.1.1. Condiciones de las matrices \(S\)

Para establecer la condiciones de las matrices \(S\), utilizamos que la ec. de Dirac debe ser válida para los campos transformados.

Esto es:

\[ (i\gamma^\mu \partial_\mu - m) \, S \, \Psi(\Lambda^{-1} x) = 0 \]

Si definimos \(y = \Lambda^{-1} x, \; y^\mu = (\Lambda^{-1})^\mu_{\;\; \nu} x^{\nu}\), el término:

\[ \partial_\mu (S \Psi(y)) = S \frac{\partial \Psi(y)}{\partial x^\mu} = S \frac{\partial \Psi(y)}{\partial y^\nu} \frac{\partial y^\nu}{\partial x^\mu} = S \, \frac{\partial \Psi(y)}{\partial y^\nu} \, (\Lambda^{-1})^\nu_{\;\; \mu} \]

La ecuación de Dirac queda:

\[ i \gamma^\mu S (\Lambda^{-1})^\nu_{\;\;\mu} \frac{\partial \Psi(y)} {\partial y^\nu} - m S \Psi(y) = 0 \]

Si multiplicamos por \(S^{-1}\) por la izquierda.

\[ i S^{-1} \gamma^\mu S \; (\Lambda^{-1})^\nu_{\;\;\mu} \frac{\partial \Psi(y)}{\partial y^\nu} - m \Psi(y) = 0 \]

Si imponemos que \(\Psi(y)\) cumple la ecuación de Dirac en coordenadas \(y\), esto es:

\[ i \gamma^\nu \frac{\partial \Psi(y)}{\partial y^\nu} - m \Psi(y) = 0 \]

se cumple:

\[ S^{-1} \gamma^\mu S \; (\Lambda^{-1})^\nu_{\;\;\mu} = \gamma^\nu \]

Si multiplicamos por la derecha por \(\Lambda\), esto es por \(\Lambda^{\rho}_{\;\; \nu}\):

\[\begin{split} S^{-1} \gamma^\mu S \; (\Lambda^{-1})^\nu_{\;\;\mu} \Lambda^{\rho}_{\;\; \nu} = \gamma^\nu \, \Lambda^{\rho}_{\;\; \nu} \\ S^{-1} \gamma^\mu S \, \delta^\rho_{\;\;\mu} = \Lambda^{\rho}_{\;\; \nu} \, \gamma^\nu \\ \end{split}\]

Notar que los valores de \(\Lambda^{\rho}_{\;\;\nu}\) son coeficientes que multiplican a la matrices \(\gamma^\nu\), y así obtenemos finalmente:

\[ S^{-1} \gamma^\mu S = \Lambda^\mu_{\;\;\nu}\gamma^\nu \]

Esta ecuación nos dice las condiciones que deben cumplir las matrices \(S\) para ser la representación de las transformaciones de Lorentz \(\Lambda\).

8.4.2. Generadores de boost y rotaciones

Vamos a determinar ahora los generadores de las transformaciones de Lorentz en el espacio de los espinores.

Las matrices \(S\) se generan nuevamente a partir de sucesivas transformaciones infinitesimales. Cada una de ellas estará definida a partir de unos generadores asociados a las rotaciones o al boost, de forma similar a como sucede con el espacio espacio-temporal.

8.4.2.1. generadores de los boosts

Consideremos un boost \(\eta\) infinitesimal en \(z\). La matriz de Lorentz asociada es:

\[ \Lambda(\eta) = I + i \eta K_3 \]

donde \(K_3\) es el generador del boost en \(z\) en el espacio espacio-temporal.

Y la representación de boost infinitesimal en el espacio de espinores será:

\[ S(\eta) = I + i \eta \, K^S_3 \]

donde \(K^S_3\) es el generador de los boost en el espacio de los espinores.

Las condiciones de las matrices \(S\) se traducen para esta caso en:

\[\begin{split} S^{-1} \gamma^0 S = \gamma^0 + \eta \, \gamma^3\\ S^{-1}\gamma^1 S = \gamma^1 \\ S^{-1}\gamma^2 S = \gamma^2 \\ S^{-1 }\gamma^3 S = \eta \, \gamma^0 + \gamma^3 \\ \end{split}\]

De la segunda y tercera condición deducimos que \(S\) y por lo tanto \(K^S_3\) conmutan con \(\gamma^1, \gamma^2\). Con lo que podemos proponer:

\[ K^S_3 = -\alpha i \gamma^0 \gamma^3 \]

que conmuta con \(\gamma^2, \gamma^3\), y donde \(\alpha\) es una constante que vamos a determinar.

De la primera condición:

\[ (I - \eta \, \alpha \gamma^0\gamma^3) \gamma^0 (I + \eta \, \alpha \gamma^0 \gamma^3) = \gamma^0 + \gamma^3 \eta \]

Si en la parte de la izquierda de la ecuación trasladamos \(\gamma^0\) del centro a la izquierda, usando las propiedades de conmutación de las \(\gamma\), obtenemos:

\[ \gamma^0 \, (I + \eta \, \alpha \gamma^0\gamma^3)^2 = \gamma^0 + \gamma^3 \eta \]

Multiplicando por \(\gamma^0\) por la izquierda, desarrollando el cuadrado, y despreciando términos en \(\eta^2\) al tratarse de un boost infinitesimal:

\[ (I + \eta \, 2 \alpha \gamma^0\gamma^3) = I + \eta \gamma^0 \gamma^3 \]

De donde concluimos que:

\[ K^S_3 = - \frac{1}{2} i \gamma^0 \gamma^3 \]

8.4.2.2. generadores de rotaciones

Consideremos ahora una rotación infinitesimal \(\theta\) a lo largo del eje \(z\).

La transformación infinitesimal en el espacio espacio-temporal viene dada por:

\[ \Lambda(\theta) = I +i \theta \, J_3 \]

Mientras que en el espacio de espinores:

\[ S(\theta) = I +i \theta \, J^S_3 \]

Las condiciones que deben cumplir son:

\[\begin{split} S^{-1} \gamma^0 S = \gamma^0 \\ S^{-1}\gamma^1 S = \gamma^1 - \theta \, \gamma^2 \\ S^{-1}\gamma^2 S = \theta \, \gamma^1 + \gamma^2 \\ S^{-1 }\gamma^3 S = \gamma^3 \\ \end{split}\]

Vemos que \(S\) , y por lo tanto \(J^S_3\) deben conmutar con \(\gamma^0, \, \gamma^3\), luego podemos suponer que:

\[ J^S_3 = -\alpha i \gamma^1\gamma^2 \]

donde \(\alpha\) es de nuevo una constante.

De la segunda condición, obtenemos:

\[ (I - \theta \, \alpha \gamma^1 \gamma^2) \gamma^1 (I + \theta \, \alpha \gamma^1 \gamma^2) = \gamma^1 - \theta \, \gamma^2 \]

Transladando \(\gamma^1\) en la parte de la izquierda de la igualdad a la izquierda, y usando las reglas de conmutación de las matrices \(\gamma\):

\[ \gamma^1 \, (I + \theta \, \alpha \gamma^1 \gamma^2)^2 = \gamma^1 - \theta \, \gamma^2 \]

Multiplicando ambos lados por \(\gamma^1\) y recordando que \((\gamma^1)^2 = -I\)

\[ (I + 2 \theta \, \alpha \gamma^1 \gamma^2) = I + \theta \gamma^1\gamma^2 \]

Obtenemos que:

\[ J^S_3 = - \frac{1}{2} i \gamma^1\gamma^2 \]

Los generadores, \(J_s, K_3\) en la representación de Pauli-Dirac.

\[\begin{split} K^S_3 = -\frac{1}{2} i \gamma^0 \gamma^3 = -\frac{1}{2} i \begin{pmatrix} I & 0 \\ 0 & - I \end{pmatrix} \begin{pmatrix} 0 & \sigma_3 \\ -\sigma_3 & 0 \end{pmatrix} = - \frac{1}{2} i \begin{pmatrix} 0 & \sigma_3 \\ \sigma_3 & 0 \end{pmatrix} \end{split}\]

\[\begin{split} J^S_3 = - \frac{1}{2} i \gamma^1\gamma^2 = - \frac{1}{2} i \begin{pmatrix} 0 & \sigma_1 \\ -\sigma_1 & 0 \end{pmatrix} \begin{pmatrix} 0 & \sigma_2 \\ -\sigma_2 & 0 \end{pmatrix} = - \frac{1}{2} \begin{pmatrix} \sigma_3 & 0 \\ 0 & \sigma_3 \end{pmatrix} = - \frac{1}{2}\Sigma_3 \end{split}\]

De forma similar daríamos el resto de rotaciones y boost, obtenemos

\[ K^S_i = -\frac{1}{2}i \gamma^0\gamma^i, \;\; J^S_k = -\epsilon_{ijk} \, \frac{1}{2} i \gamma^i\gamma^j \]

donde \(i \lt j, \, i, j = 1, 2, 3\).

De tal forma que recuperamos los generadores en \(z\) y podemos dar además los de \(x, y\).

Vemos que el generador de las rotaciones en el espacio de los espinores es el espín

\[ {\bf S} = \frac{1}{2} {\bf \Sigma} \]

8.4.3. Representaciones espinoriales de boosts y rotaciones.

Calculemos ahora la representación espinorial, \(S(\eta)\), de un boost \(\eta\) en \(z\)

Que obtendríamos de la sucesión de transformación infinitesimales, esto es:

\[\begin{split} S(\eta) = e^{i \eta K^S_3} = e^{\frac{\eta}{2} \gamma^0\gamma^3} \equiv \sum_{k= 0}^\infty \frac{1}{k!} \left(\frac{\eta}{2} \right)^k \begin{pmatrix} 0 & \sigma_3 \\ \sigma_3 & 0 \end{pmatrix}^k \end{split}\]

Dado que

\[\begin{split} \begin{pmatrix} 0 & \sigma_3 \\ \sigma_3 & 0 \end{pmatrix}^2 = \begin{pmatrix} I & 0 \\ 0 & I \end{pmatrix} \end{split}\]

podemos separar los términos pares e impares de la sucesión:

\[\begin{split} S(\eta) = \sum_{k= 0}^\infty \left(\frac{\eta}{2}\right)^{2k} \frac{1}{2k!} \begin{pmatrix} I & 0 \\ 0 & I \end{pmatrix} + \sum_{k= 0}^\infty \left(\frac{\eta}{2}\right)^{2k+1} \frac{1}{(2k+1)!} \begin{pmatrix} 0 & \sigma_3 \\ \sigma_3 & 0 \end{pmatrix} \end{split}\]

Y podemos expresar \(S(\eta)\) como:

\[\begin{split} S(\eta) = \cosh \frac{\eta}{2} \begin{pmatrix} I & 0 \\ 0 & I \end{pmatrix} + \sinh \frac{\eta}{2} \begin{pmatrix} 0 & \sigma_3 \\ \sigma_3 & 0 \end{pmatrix} = \\ \cosh \frac{\eta}{2} \, I + \gamma^0\gamma^3 \, \sinh \frac{\eta}{2} \end{split}\]

O simplemente:

\[\begin{split} S(\eta) = \begin{pmatrix} \cosh \frac{\eta}{2} I & \sinh \frac{\eta}{2} \sigma_3 \\ \sinh \frac{\eta}{2} \sigma_3 & \cosh \frac{\eta}{2} I \end{pmatrix} \end{split}\]

Que podemos reescribir en una expresión más conocida, si usamos las relaciones trigonométricas hyperbólicas:

\[ \cosh \frac{\eta}{2} = \sqrt{\frac{\cosh \eta + 1}{2}} = \sqrt{\frac{\gamma+1}{2}}, \;\; \sinh \frac{\eta}{2} = \text{sign}(\eta) \, \sqrt{\frac{\cosh \eta-1}{2}} = \text{sign}(\eta) \, \sqrt{\frac{\gamma-1}{2}} \]

Si introducimos que \(E = \gamma m\), obtenemos las siguientes relaciones:

\[ \sqrt{\frac{\gamma+1}{2}} = \sqrt{\frac{E+m}{2m}}, \;\; \sqrt{\frac{\gamma-1}{\gamma+1}} = \sqrt{\frac{E-m}{E+m}} = \frac{\sqrt{E^2-m^2}}{E+m} = \frac{p}{E+m} = \kappa \]

Asi pues, la matriz \(S\), al hacer un boost en la dirección \(z\), queda:

\[\begin{split} S(\beta) = \sqrt{\frac{E+m}{2m}} \begin{pmatrix} I & \kappa \, \sigma_3 \\ \kappa \, \sigma_3 & I \end{pmatrix} \end{split}\]

Si aplicamos un boost sobre un espinor en reposo, \(u_s(m)\), el espinor que obtendríamos sería, \(u_s(p)\):

\[ u_s(p) = S(\beta) \, u_s(m), \]

Esto es:

\[\begin{split} u_s(p) = \sqrt{\frac{E+m}{2m}} \begin{pmatrix} I & \kappa \, \sigma_3 \\ \kappa \, \sigma_3 & I \end{pmatrix} \, \sqrt{2m} \begin{pmatrix} \chi_s \\ 0 \end{pmatrix} = \sqrt{E+m} \begin{pmatrix} \chi_s \\ \kappa \sigma_3 \chi_s \end{pmatrix} \end{split}\]

que es el espinor \(u_s(p)\) para un fermión en movimiento en la dirección \(z\), que hemos obtenido en la extensión [ext-Dirac].

Ejercicio: Comprobar que \(S(\eta)\) cumple las condiciones de las matrices \(S\)

Por similitud, las matrices \(S(\eta_i)\) que representan a los boosts en las tres posibles direcciones, \(\eta_i, \, i = 1, 2, 3\), son:

\[\begin{split} S(\eta_i) = e^{i \eta_i K^S_i } = e^{\frac{\eta_i}{2} \gamma^0\gamma^i } = \begin{pmatrix} \cosh \frac{\eta_i}{2} I & \sinh \frac{\eta_i}{2} \sigma_i \\ \sinh \frac{\eta_i}{2} \sigma_i & \cosh \frac{\eta_i}{2} I \end{pmatrix} \end{split}\]

Y si hacemos un boost con rapidez \(\eta\) en la dirección \(\hat{{\bf v}}\):

\[\begin{split} S(\eta \, \hat{{\bf v}}) = \begin{pmatrix} \cosh \frac{\eta}{2} I & \sinh \frac{\eta}{2} \, (\vec{\sigma} \cdot \hat{{\bf v}}) \\ \sinh \frac{\eta}{2} \, ({\vec \sigma} \cdot \hat{{\bf v}}) & \cosh \frac{\eta}{2} I \end{pmatrix} = \\ \end{split}\]

Esto es:

\[\begin{split} S(\beta \hat{\bf v}) = \sqrt{\frac{E+m}{2m}} \begin{pmatrix} I & \kappa \, (\vec{\sigma} \cdot \hat{{\bf v}}) \\ \kappa \, (\vec{\sigma} \cdot \hat{\bf v}) & I \end{pmatrix} \end{split}\]

Determinemos ahora las matrices \(S(\theta)\) asociadas a una rotación \(\theta\) alrededor de \(z\):

\[ S(\theta) = e^{i \theta J^S_s} = e^{-i \theta S_3} = e^{-i \frac{\theta}{2} \Sigma_3} \]

A partir de:

\[ S(\theta) = e^{-i \frac{\theta}{2} \Sigma_3} = \sum_{k=0} \frac{1}{k!} \left(\frac{-i\theta}{2} \right)^k (\Sigma_3)^k \]

separando en términos pares e impares

\[ \sum_{k=0} (-1)^k \frac{1}{2k!}\left(\frac{\theta}{2}\right)^{2k} I - i \sum_{k=0} (-1)^k \frac{1}{(2k+1)!} \left(\frac{\theta}{2}\right)^{2k+1} \Sigma_3 \]

usando:

\[ (\Sigma_k)^{2k} = I, \;\; (\Sigma_3)^{2k+1} = \Sigma_3 \]

Obtenemos:

\[\begin{split} S(\theta) = \begin{pmatrix} e^{-i\frac{\theta}{2} \sigma_3} & 0 \\ 0 & e^{-i\frac{\theta}{2} \sigma_3} \end{pmatrix} = \begin{pmatrix} \cos \frac{\theta}{2} I - i \sin \frac{\theta}{2} \sigma_3 & 0 \\ 0 & \cos \frac{\theta}{2} I - i \sin \frac{\theta}{2} \sigma_3 \end{pmatrix} \end{split}\]

Para una rotación de un ángulo \(\theta\) alrededor de un eje dado por \(\hat{{\bf n}}\) en sentido anti-horario, la expresión de \(S\) es:

\[ S(\theta \, \hat{\bf n}) = e^{-i\frac{\theta}{2} \hat{\bf n} \, {\bf \Sigma}} = \cos \frac{\theta}{2} I - i \sin \frac{\theta}{2} (\hat{\bf n} \cdot {\bf \Sigma}) \]

O simplemente:

\[\begin{split} S(\theta \, \hat{\bf n}) = \begin{pmatrix} e^{-i\frac{\theta}{2} \, (\hat{{\bf n}} \cdot {\vec \sigma})} & 0 \\ 0 & e^{-i\frac{\theta}{2} \, (\hat{{\bf n}} \cdot {\vec \sigma})} \end{pmatrix} \end{split}\]

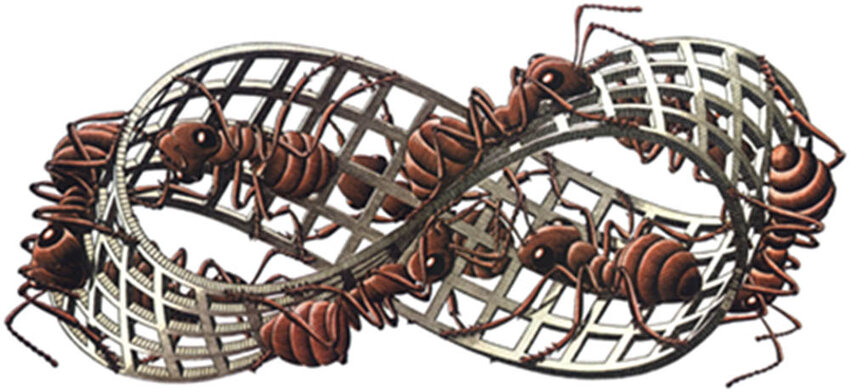
Vemos que para \(\theta = 2 \pi\) tenemos \(S(2\pi ) = -I\), y que hacen falta dos vueltas completas, \(\theta = 4 \pi\), para regresar a la identidad \(S(4\pi) = I\).

¡La rotación de un espinor es diferente a la de un vector!

El nombre de espinor viene precisamente del hecho de hacen falta dos vueltas completas para regresar al estado original.

También observamos que los dos bi-espinores del espinor de Dirac se transforman igual pero independientemente, sin afectar uno a otro.

La siguiente figura muestra un dibujo de Escher en el que una hormiga (el espín) tiene que realizar dos vueltas (\(4\pi\) para el espín) en la cinta de Moebius para regresar a su estado inicial. Si la hormiga solo da una vuelta, queda invertida, igual que el espín bajo una rotación de \(2\pi\).

Hormiga en una cita de Moebius por Escher

Recopilemos: de forma genérica podemos dar ahora la representación \(S\) de una rotación \(\theta\) alrededor de un eje \(\hat{{\bf n}}\) en sentido anti-horario y un boost de rapidez \(\eta\) en dirección \(\hat{{\bf v}}\) como:

\[ S(\theta \, \hat{{\bf n}}, \, \eta \hat{{\bf v}}) = e^{+i \theta \, \hat{{\bf n}} \cdot {\bf S} + i \eta \, \hat{{\bf v}} \cdot {\bf K^S} } \]

Ejercicio: A partir de las expresiones de los generadores en la representación Pauli-Dirac comprueba las reglas de conmutación:

\[ [S_i, S_j] = i\epsilon_{ijk} S_k, \; [K^S_i, K^S_j] = -i\epsilon_{ijk} S_k, \; [S_i, K^S_j] = i\epsilon_{ijk} K^S_k \]

Ejercicio: Rota el espinor en reposo \(u_1(m)\) respecto al eje \(y\) por un ángulo \(\theta\), y verifica que se trata del espinor cuyo espín entá alineado en la dirección donde queda el vector \({\hat k}\) tras la rotación.

8.4.4. No unitariedad de los boosts

Una último apunte importante: Las transformaciones de los boost no son unitarias, pero sí las rotaciones.

Para que la transformación, \(S\), sea unitaria debe cumplir

\[ S^{-1} = S^\dagger, \;\; S^\dagger \, S = I \]

Véamoslo con la expresión infinitesimal, (aunque puede verse igualmente con la expresión explícita \(S(\eta)\)).

La transformación inversa es \(S^{-1}(\eta) = S(-\eta)\), que viene de exigir que al hacer la transformación inversa obtenemos la identidad, lo que para la representación se traduce

\[ S(\Lambda^{-1}) \, S(\Lambda) = I, \;\; S(\Lambda^{-1}) = S^{-1}(\Lambda) \]

Si hacemos el traspuesto conjungado de \(S(\eta)\) para un boost, \(\eta\), infinitesimal en \(z\). $\( S^\dagger(\eta) = I + \frac{\eta}{2} (\gamma^0 \gamma^1)^\dagger = I + \frac{\eta}{2} (\gamma^1)^\dagger (\gamma^0)^\dagger = \\ I + \frac{\eta}{2} (-\gamma^1)(\gamma^0) = I + \frac{\eta}{2} (\gamma^0\gamma^i) = S(\eta) \)$

Luego:

\[ S^{-1}(\eta) \neq S^\dagger(\eta) \]

Esto tendrá consecuencias relevantes dado que el término \(\Psi^\dagger(x) \Psi(x)\) no será invariante Lorentz.

Sin embargo, las rotaciones sí respetan unitariedad:

\[ S^{-1}(\theta) = S(-\theta) = S^\dagger(\theta) \]

Veámoslo con una rotación \(\theta\) infinitesimal alrededor de \(z\),

\[\begin{split} S^\dagger(\theta) = I + \frac{\theta}{2} (\gamma^1\gamma^2)^\dagger = I + \frac{\theta}{2} (\gamma^2)^\dagger(\gamma^1)^\dagger = \\ I + \frac{\theta}{2} (-\gamma^2)(-\gamma^1) = I + \frac{\theta}{2} \gamma^2\gamma^1 \\ I - \frac{\theta}{2} \gamma^1 \gamma^2 = S(-\theta) = S^{-1}(\theta) \end{split}\]

Luego las rotaciones si son transformaciones unitarias en el espacio de los espinores.

8.5. Norma y corriente de espinores

En mecánica cuántica definimos una densidad de probabilidad, asociada a la norma de la función de ondas, \(|\psi(x)|^2 = \psi^*(x) \psi(x)\), y una corriente de probabilidad conservada.

La expresión similar que obtenemos con espinores de Dirac, \(|\Psi(x)|^2 = \Psi^\dagger(x) \Psi(x)\), no es un invariante Lorentz, y nos obliga a introducir el espinor adjunto:

\[ \bar{\Psi}(x) = \Psi^\dagger(x) \, \gamma^0 \]

A partir de aquí, podemos construir dos de las formas bilineales:

• la norma, \(\bar{\Psi}\Psi\) que es un escalar Lorentz.

• la corriente de probabilidad o fermiónica, \(\bar{\Psi}(x) \gamma^\mu \Psi(x)\) que es un vector bajor Lorentz

Vamos a verificar en esta sección el comportamiento bajo Lorentz de la norma y de la corriente.

8.5.1. Norma

El término

\[ \Psi^\dagger \Psi = |\psi_1|^2 + |\psi_2|^2 + |\psi_2|^2 + |\psi_4|^2 \]

está asociado a la densidad de probabilidad, es siempre una cantidad positiva.

Sin embargo no es un invariante Lorentz, debido a que las matrices que representan el boost en el espacio de los espinores no son unitarias.

Sabemos que:

\[ S^{-1}(\eta) = S(-\eta) \neq S^\dagger (\eta) \]

Por lo tanto la transformación por boost del término \(\Psi^\dagger(x) \Psi(x)\),

\[\begin{split} \Psi^\dagger(x) \Psi(x) \to \Psi'^\dagger(x) \Psi'(x) = \\ \Psi^\dagger(y) S^{\dagger}(\eta) S(\eta) \Psi(y) \neq \Psi^\dagger(y) \Psi(y) \end{split}\]

con \(y = \Lambda^{-1} x\), no es invariante Lorentz.

Para definir la corriente de probabilidad introducimos el espinor adjunto:

\[ \bar{\Psi}(x) = \Psi^\dagger(x) \gamma^0 \]

En la representación de Pauli-Dirac:

\[ \bar{\Psi}(x) = (\psi^*_1(x), \psi^*_2(x), -\psi^*_3(x), -\psi^*_4(x)), \]

que tiene forma de vector fila.

Veremos ahora que término \(\bar{\Psi}(x)\Psi(x)\) es un invariante Lorentz y es unitario.

Hemos visto que para boosts, \(S(\eta)\) no es unitaria, pero que \(S(\theta)\), asociada a las rotaciones, sí lo es.

\[\begin{split} S^{-1}(\eta) = \gamma^0 S^\dagger(\eta) \gamma^0 \neq S^{\dagger}(\eta) \\ S^{-1}(\theta) = \gamma^0 S^\dagger(\theta) \gamma^0 = S^\dagger(\theta) \end{split}\]

Veamos que \(\bar{\Psi}(x) \Psi(x)\) es un escalar Lorentz:

\[\begin{split} \bar{\Psi}(x) \Psi(x) \to \bar{\Psi}'(x) \Psi'(x) = \\ (S \, \Psi(y))^\dagger \gamma^0 (S \, \Psi(y)) = \Psi^\dagger(y) \, S^{\dagger} \gamma^ 0 S \, \Psi(y) = \Psi^\dagger(y) \gamma^0 (\gamma^0 S^{\dagger} \gamma^ 0) S \, \Psi(y) = \\ \Psi^\dagger(y) \gamma^0 (S^{-1} S) \Psi(y)) = \Psi^\dagger(y) \gamma^0 \Psi(y) = \bar{\Psi}(y) \Psi(y) \end{split}\]

donde \(y = \Lambda^{-1} x\).

Cuestión: Verifica que \(\bar{\Psi}(x) \Psi(x) = 2 m\), (por convención) para las soluciones de la ec. de Dirac.

8.5.2. Corriente fermiónica

La corriente de probabilidad fermiónica es un cuadrivector dado por:

\[ \bar{\Psi} \gamma^\mu \Psi = (\rho, {\bf j}) \]

Vamos a comprobar ahora que \(\bar{\Psi}(x) \gamma^\mu \Psi(x)\) es un cuadri-vector y que se transforma como tal bajo transformaciones Lorentz.

Si aplicamos una transformación de Lorentz, con representación espinorial \(S\), la corriente transforma como:

\[ \bar{\Psi} \gamma^\mu \Psi \to \bar{\Psi}'(x) \gamma^\mu \Psi'(x) = \Psi(y)^\dagger S^\dagger \, \gamma^0 \gamma^\mu \, S \Psi(y) \]

con \(y = \Lambda^{-1} x\).

Que la corriente se transforme como un vector implica que:

\[ \bar{\Psi}'(x) \gamma^\mu \Psi'(x) = \Lambda^{\mu}_{\;\;\nu} \, \bar{\Psi}(y) \gamma^\nu \Psi(y) \]

Esto es:

\[\begin{split} \Psi^\dagger(y) \, S^\dagger \gamma^0 \gamma^\mu S \, \Psi(y) = \Lambda^{\mu}_{\;\;\nu} \, \Psi^\dagger(y) \gamma^0 \gamma^\nu \Psi(y) \\ \end{split}\]

O que se cumple:

\[ S^\dagger \gamma^0 \gamma^\mu \, S = \Lambda^{\mu}_{\;\;\nu} \gamma^0 \gamma^\nu \]

En la parte derecha de la ecuación, haciendo uso \(S^\dagger \gamma^0 = \gamma^0 S^{-1}\),

\[ \gamma^0 S^{-1} \gamma^\mu S \]

Y aplicando las condiciones de las matrices \(S\), esto es, \(S^{-1} \gamma^\mu S = \Lambda^\mu_{\;\;\nu}\gamma^\nu \)

nos queda:

\[ \Lambda^{\mu}_{\;\;\nu} \gamma^0 \gamma^\nu \]

Luego, efecticamente, \(\bar{\Psi}(x) \gamma^\mu \Psi(x)\) se comporta como vector con respecto a las transformaciones Lorentz.

8.6. Inversión bajo paridad

La inversión de paridad invierte la coordenadas especiales, \({\bf x } \to -{\bf x}\). Es una transformación de Lorentz porque preserva el producto escalar de cuadrivectores.

La matriz de la representación, \(\Lambda(P)\) debe invertir las coordenadas espaciales, esto es:

\[ x'^\mu = \Lambda^{\mu}_{\;\;\nu}(P) \, x^\nu \]

luego:

\[\begin{split} \Lambda(P) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \end{split}\]

Es una transformación impropia dado que su determinante es -1. $\( \det(\Lambda) = -1 \)$

8.6.1. representación espinorial

La matriz que representa en el espacio de espinores la inversión por paridad, \(S(P)\),

\[ \Psi(x) \to \Psi(x^0, {\bf x}) = S(P) \, \Psi(x^0, -{\bf x}) \]

debe cumplir (por las condiciones de las matrices \(S\):

\[\begin{split} S^{-1}\gamma^0 S = \gamma^0, \\ S^{-1}\gamma^1 S = -\gamma^1, \\ S^{-1}\gamma^2 S = -\gamma^2, \\ S^{-1}\gamma^3 S = -\gamma^3. \\ \end{split}\]

Esto es, si multiplicamos por \(S\) a ambos lados de la igualdad por la izquierda:

\[ \gamma^0 S = S \gamma^0, \;\; \gamma^i S = - S \gamma^{i} \]

La matriz que cumple esta condición es:

\[ S(P) = \gamma^{0} \]

La matriz \(S\) podría incluir una pase compleja, pero por convención se tomó como 1.

Si aplicamos paridad sobre los espinores nos encontramos:

\[\begin{split} u_s(E, {\bf p}) \to S(P) \, u_s(E, -{\bf p}) = + \, u_s(E, {\bf p}), \\ v_s(E, {\bf p}) \to S(P) \, v_s(E, -{\bf p}) = - \, v_s(E, {\bf p}), \;\; \end{split}\]

Los espinores en reposo son autoestados de paridad, los de los fermiones, \(u_s(m, {\bf 0})\), tienen paridad positiva, mientras que los de los antifermiones \(v_s(m, {\bf 0})\), negativa.

8.6.2. comportamiento de las formas bilineales

Vamos a verificar que la paridad afecta de la siguiente forma a las formas bilineales principales:

\(\bar{\Psi} \Psi\)	escalar
\(\bar{\Psi} \gamma^5 \Psi\)	pseudo-escalar
\(\bar{\Psi} \gamma^\mu \Psi \)	vectorial
\(\bar{\Psi} \gamma^\mu \gamma^5 \Psi\)	vector axial

A partir del hecho que: $\( S^{-1} \gamma^5 S = \gamma^5, \;\; \gamma^5 S = S \gamma^5 \)$

es sencillo comprobar que \(\bar{\Psi}(x) \gamma^5 \Psi(x)\) y \(\bar{\Psi}(x) \gamma^\mu \gamma^5 \Psi(x)\) se transforman frente a boosts y rotaciones como un escalar y un vector respectivamente.

Vamos a ver como se comportan con respecto a la inversión por paridad.

Recordemos que la representación espinorial de la inversión de paridad es simplemente, \(S(P) = \gamma^0\).

8.6.2.1. norma escalar

Apliquemos inversión de paridad a \(\bar{\Psi}(x) \Psi(x)\):

\[\begin{split} \bar{\Psi}(x) \Psi(x) \to (S \Psi(y))^\dagger \gamma^0 (S \Psi(x)) = \\ \Psi^\dagger(y) (\gamma^0)^\dagger \gamma^0 \gamma^0 \Psi(y) = \Psi^\dagger(y) \gamma^0 \Psi(y) = \bar{\Psi}(y) \Psi(y) \end{split}\]

donde \(y = \Lambda^{-1}x\).

Por lo tanto \(\bar{\Psi}(x) \Psi(x)\) es un escalar bajo paridad.

8.6.2.2. pseudo-escalar

Apliquemos inversión de paridad ahora a \(\Psi(x) \gamma^5 \Psi(x)\):

\[\begin{split} \bar{\Psi}(x) \gamma^5 \Psi(x) \to (S \Psi(y))^\dagger \gamma^0 \gamma^5 (S \Psi(y)) = \\ \Psi^\dagger(y) (\gamma^0)^\dagger \gamma^0 \gamma^5 \gamma^0 \Psi(y) = \Psi^\dagger(y) \gamma^5 \gamma^0 \Psi(y) = \\ - \Psi^\dagger(y) \gamma^0 \gamma^5 \Psi(y) = - \bar{\Psi}(y) \gamma^5 \Psi(y) \end{split}\]

donde \(y = \Lambda^{-1}x\).

Por lo tanto \(\Psi(x) \gamma^5 \Psi(x)\) es un pseudo-escalar bajo paridad.

8.6.2.3. corriente vectorial

Aplicamos inversión de paridad a la corriente \(\bar{\Psi}(x) \gamma^\mu \Psi(x)\):

\[\begin{split} \bar{\Psi}(x) \gamma^\mu \Psi(x) \to (S \Psi(y))^\dagger \gamma^0 \gamma^\mu (S \Psi(y)) = \\ \Psi^\dagger(y) (\gamma^0)^\dagger \gamma^0 \gamma^\mu \gamma^0 \Psi(y) = \Psi^\dagger(y) \gamma^\mu \gamma^0 \Psi(y) \end{split}\]

donde \(y= \Lambda^{-1}x\).

para \(\mu = 0\)

\[ (\Psi^\dagger(y) \gamma^0) \gamma^0 \Psi(y) = \bar{\Psi}(y) \gamma^0 \Psi(y) \]

para los índices espaciales, \(k = 1, 2, 3\).

\[ \Psi^\dagger(y) \gamma^k \gamma^0 \Psi(y) = - (\Psi^\dagger(y) \gamma^0) \gamma^k \Psi(y) = - \bar{\Psi}(y) \gamma^k \Psi(y) \]

Luego bajo paridad:

\[\begin{split} \bar{\Psi}(x) \gamma^\mu \Psi(x) = (\bar{\Psi}(x) \gamma^0 \Psi(x), \bar{\Psi}(x) \gamma^k \Psi(x)) \to \\ \bar{\Psi}'(x) \gamma^\mu \Psi'(x) = (\bar{\Psi}(y) \gamma^0 \Psi(y), -\bar{\Psi}(y) \gamma^k \Psi(y)) \end{split}\]

La componente temporal no cambia de signo, pero si las espaciales, que es justamente la operación de paridad sobre un cuadri-vector.

Luego \(\Psi(x) \gamma^\mu\Psi(x)\) es un vector bajo paridad.

8.6.2.4. corriente axial

Aplicamos ahora inversión de paridad a \(\bar{\Psi}(x) \gamma^\mu \gamma^5 \Psi(x)\):

\[\begin{split} \bar{\Psi}(x) \gamma^\mu \gamma^5 \Psi(x) \to (S \Psi(y))^\dagger \gamma^0 \gamma^\mu \gamma^5 (S \Psi(y)) = \\ \Psi^\dagger(y) (\gamma^0)^\dagger \gamma^0 \gamma^\mu \gamma^5 \gamma^0 \Psi(y) = \Psi^\dagger(y) \gamma^\mu \gamma^5 \gamma^0 \Psi(y) = - \Psi^\dagger(y) \gamma^\mu \gamma^0 \gamma^5 \Psi(y) \end{split}\]

Reencontramos la misma situación que antes, al intercambair \(\gamma^\mu\gamma^0 \to \gamma^0 \gamma^\mu\), la parte temporal no introduce cambio de signo \(\mu = 0\), pero si la espacial, \(k = 1, 2, 3\).

Así pues:

\[\begin{split} \bar{\Psi}(x) \gamma^\mu \gamma^5 \Psi(x) = (\bar{\Psi}(x) \gamma^0 \gamma^5 \Psi(x), \bar{\Psi}(x) \gamma^k \gamma^5 \Psi(x)) \to \\ \bar{\Psi}'(x) \gamma^\mu \gamma^5 \Psi'(x) = (-\bar{\Psi}(y) \gamma^0 \gamma^5\Psi(y), \bar{\Psi}(y) \gamma^k \gamma^5 \Psi(y)) \\ \end{split}\]

Cambia de signo la parte temporal pero no la espacial.

Luego \(\Psi(x) \gamma^\mu \gamma^5 \Psi(x)\) se comporta como un vector axial bajo paridad.

8.7. Inversión de carga

La inversión de carga consiste en invertir las cargas de una partícula.

\[ q \to -q \]

pero no cambiamos las coordenadas \(t, {\bf x}\).

Esta inversión es la misma que cambiar partícula por antipartícula. Dado que las antipartículas son partículas con las cargas opuestas.

8.7.1. representación espinorial

La operación de inversión de carga cambia las soluciones de Dirac de fermiones a anti-fermiones, \(\Psi(x) \to \Phi(x)\) (con la excepción de una posible fase).

Para cambiar la parte espacio-temporal, la operación debe incluir el complejo conjugado.

La operación de carga tiene la expresión:

\[ \Psi(x) \to S(C) \, \Psi^*(x) \]

Donde \(S(C)\) es la matriz que representa la inversión de carga en el espacio espinorial.

Si exigimos que la ecuación de Dirac sea válida para \(S \, \Psi^*(x)\):

\[ (i \gamma^{\mu} S \partial_\mu - m) \,S \, \Psi^*(x) = 0 \]

Si multiplicamos por la izquierda por \(S^{-1}\) obtenemos:

\[ (i S^{-1} \gamma^{\mu} S \partial_\mu - m)\, \Psi^*(x) = 0 \]

Por otro lado, si tomamos el complejo conjugado de la ecuación de Dirac inicial:

\[ (-i (\gamma^\mu)^* \partial_\mu - m) \, \Psi^*(x) = 0 \]

Para que ambas sean iguales debe cumplirse que:

\[ S^{-1} \gamma^\mu S = - (\gamma^\mu)^* \]

En la representación de Pauli-Dirac, la única matriz \(\gamma^\mu\) que cambia al aplicar el complejo conjugado es \((\gamma^2)^* = - \gamma^2\), asi pues, las condiciones anteriores se traducen en:

\[\begin{split} S^{-1}\gamma^0 S = - \gamma^0, \\ S^{-1}\gamma^1 S = - \gamma^1, \\ S^{-1}\gamma^2 S = \gamma^2, \\ S^{-1}\gamma^3 S = - \gamma^3. \end{split}\]

Y la matriz que las cumple es:

\[ S(C) = i \gamma^2 \]

Donde el factor \(i\) es una convención, que permite que la matriz \(S\) sea real.

\[\begin{split} i \gamma^2 = i \begin{pmatrix} 0 & 0 & 0 & -i \\ 0 & 0 & i & 0 \\ 0 & i & 0 & 0 \\ -i & 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & -1 & 0 \\ 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} \end{split}\]

Ejercicio: Verifica que la conjugación de carga cambia \(\Psi_i(x) \to \Phi_i(x)\). Usa los espinores autoestados de helicidad que se deplazan en la dirección \(z\)

8.7.2. interacción con el campo electromagnético.

Para incluir la interacción del fermión con carga \(q\) con un campo electromagnético \(A_\mu\) modificamos de forma mínima la ecuación de Dirac:

\[ \left[\gamma^\mu (i\partial_\mu - q A_\mu) - m \right] \, \Psi(x) = 0 \]

Vamos a transformar las soluciones de fermiones en las de antifermiones y ver cómo queda la interacción con el campo \(A_\mu\).

Si tomamos el complejo conjugado y multiplicamos por \(i\gamma^2\) por la izquierda:

\[ i\gamma^2 \left[-i (\gamma^\mu)^* \partial_\mu - q (\gamma^\mu)^* A_\mu - m \right] \, \Psi^*(x) = 0 \]

Aplicando las reglas de conmutación de las matrices \(\gamma^2 \gamma^\mu\) y el hecho de que bajo el conjugado solo cambia \((\gamma^2)^* = - \gamma^2\), obtenemos:

\[\begin{split} \left[i \gamma^\mu \partial_\mu + q \gamma^\mu A_\mu -m \right] \, i \gamma^2 \Psi^*(x) = 0 \\ \left[\gamma^\mu (i\partial_\mu + q A_\mu) - m \right] \, i \gamma^2 \Psi^*(x) = 0 \end{split}\]

Luego al intercambiar las gammas en \(\gamma^2(\gamma^\mu)^*\), el factor que se acopla con \(A_\mu\), se produce un cambio de signo.

Esto es la solución \(\Phi(x) = i \gamma^2 \Psi^*(x)\) tiene carga opuesta: en la ecuación de Dirac ha cambiado \(-q \to q\).

\[ \left[i\gamma^\mu(i\partial_\mu + q A_\mu) -m \right] \Phi(x) = 0 \]

8.8. Inversión temporal

La inversión temporal nos cambia \(t \to -t\), no cambia las coordenadas \({\bf x} \to {\bf x}\) pero si el momento \({\bf p} \to -{\bf p}\).

El tratamiento en mecánica cuántica de la inversión temporal require cierto cuidado matemático. Se trata de una transformación anti-unitaria, que podemos descomponer en dos, una transformación unitaria, \(T\), y la toma del complejo conjugado:

\[ \psi(t, {\bf x}) \to T \, \psi^*(-t, {\bf x}) \]

Para las soluciones de la ec. de Dirac tendremos

\[ \Psi(t, {\bf x}) \to S(T) \, \Psi^*(-t, {\bf x}) \]

Si partimos de que le ec. de Dirac debe ser válida para el estado transformado:

\[ (i \gamma^\mu \partial_\mu -m) \, S \, \Psi^*(-t, {\bf x}) = 0 \]

multiplicando por \(S^{-1}\) por la izquierda obtenemos:

\[ [i (S^{-1} \gamma^\mu S) \partial_\mu -m] \, \Psi^*(-t, {\bf x}) = 0 \]

si partimos inicialmente de la ec. de Dirac, tomamos su complejo conjugado

\[ (-i (\gamma^\mu)^* \partial_\mu - m) \Psi^*(t, {\bf x}) \]

si cambiamos ahora \(t \to -t\):

\[ (-i \Lambda^\mu_{\;\;\nu} (\gamma^\nu)^* \partial_\mu - m) \Psi^*(-t, {\bf x}) \]

donde: $\( \Lambda^\mu_{\;\;\nu} = \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \)$

Luego la condición de \(S\) es:

\[ S^{-1} \gamma^\mu S = - \Lambda^\mu_{\;\;\nu} (\gamma^\nu)^* \]

que se traduce, en la representación de Pauli-Dirac, en:

\[\begin{split} S^{-1}\gamma^0 S = \gamma^0, \\ S^{-1}\gamma^1 S = - \gamma^1, \\ S^{-1}\gamma^2 S = \gamma^2, \\ S^{-1}\gamma^3 S = - \gamma^3. \end{split}\]

que admite como solución:

\[ S = i\gamma^1\gamma^3 \]

Así la inversión por tiempo es:

\[ \Psi(t, {\bf x}) \to i\gamma^1 \gamma^3 \Psi^*(-t, {\bf x}) \]

8.9. Inversión CPT

El teorema CPT de QFT afirma que todo lagrangiano invariante Lorentz, local y hermítico, es invariante bajo la inversión conjunta de tiempo, paridad y carga, o CPT.

La consecuencia de dicho teorema es que la partículas y antipartículas tienen la carga opuesta, misma masa y mismo tiempo de vida media, lo que se ha confirmado experimentalmente hasta la fecha.

Luego CPT es una inversión exacta en la Naturaleza.

También implica que una violación de una de ellas implica a las otras dos, esto es, si se viola \(P\) se viola \(CT\).

\[ P \leftrightarrow CT, \;\; CP \leftrightarrow T \]

En el caso de los espinores de Dirac, la inversión combinada queda:

\[\begin{split} CPT : \Psi(t, {\bf x}) \to CP : i\gamma^1 \gamma^3 \Psi^*(-t, {\bf x}) \\ \to C: -i \gamma^0 \gamma^1 \gamma^3 \Psi^*(-t, -{\bf x}) \\ \to \gamma^2 \gamma^0 \gamma^1 \gamma^3 \Psi(-t, -{\bf x}) = \gamma^5 \Psi(-t, -{\bf x}) \end{split}\]

8.10. Transformación de las formas bilineales frente a C, P, T

Podemos dar la tabla de las transformaciones de las formas bilineales (a excepción de unas fases):

	C	P	T	CPT
\(x\)	\(x\)	\(t, -{\bf x}\)	\((-t, {\bf x})\)	\(-x\)
\(S \equiv \bar{\Psi}(x) \Psi(x)\)	\(S\)	\(S\)	\(S\)	\(S\)
\(P \equiv \bar{\Psi}(x) \gamma^5 \Psi(x)\)	\(P\)	\(-P\)	\(-P\)	\(P\)
\(V^\mu \equiv \bar{\Psi} \gamma^\mu \Psi\)	-\(V^\mu\)	\(V_\mu\)	\(V_\mu\)	- \(V^\mu\)
\(A^\mu \equiv \bar{\Psi} \gamma^\mu \gamma^5\Psi\)	\(A^\mu\)	-\(A_\mu\)	\(A_\mu\)	-\(A^\mu\)